竖直上升管中超临界水的宽范围换热关联式
2012-06-26刘鑫,匡波
刘 鑫,匡 波
(上海交通大学核科学与工程学院,上海200240)
作为第四代核能系统之一的超临界水冷堆具有热效率高、系统简单、经济性好等优点,已成为当前研发热点。掌握各种工况条件下超临界压力水的传热特性是超临界水冷堆研发与安全分析的重要基础。超临界水在拟临界点附近物性剧烈变化,由此导致一系列复杂流动传热机制,使得建立在常物性基础上的传统关联式准确预测其对流传热行为变得困难。前人对超临界水传热进行了大量实验研究,基于各自实验数据建立了各种关联式[1-9]。这些关联式因其所关联的数据范围有限,故适用范围有待进一步检验。为了在更宽广参数与工况范围反映超临界水的传热规律,需要结合宽广范围内的实验数据建立换热关联式,预测其包括传热恶化在内的多种传热行为。
本文针对超临界压力下水在竖直上升管内的传热工况,广泛搜集整理实验数据,建立宽范围的传热实验数据库,在对传热机理与关联形式分析讨论的基础上,建立适用于宽范围的换热关联式,用以预测多种工况下超临界压力水的传热趋势和规律。
1 宽范围数据库
本文从1963年到2011年的公开文献中搜集整理了共计16 155个超临界压力下在竖直上升管内水的传热实验数据[1,7-8,10-22]。
为了确保数据库的可信度,对收集的实验数据进行如下筛选:
首先,考虑到数据引用等多种原因导致搜集的数据中可能出现重复数据,引入欧几里得距离DE进行校核:

其中p=8,xj分别对应8个变量:直径、压力、质量流速、热流密度、入口温度、壁温、主流温度、主流焓值。当数据距离小于0.000 3时,认为这两个数据是重复的,则删除重复数据。
其次,考虑到少数实验因测量误差过大等原因对数据质量带来不良影响,由此导致Nu、换热系数等计算不准确,根据加热功率和流体焓值变化的相对差考察实验数据满足热平衡条件的不确定度:

若不确定度大于0.05,则剔除该组实验数据。
通过以上筛选,最终共删除重复数据104个、不满足热平衡条件的数据1 293个,可用数据占原始数据的91.35%。由此,所建立的实验数据库包括351组实验工况,共14 758个实验数据点。该实验数据库的传热管径D范围:0.006~0.038m,压力P范围:22.4~31.03MPa,质量流速G范围:200~3 500kg/(m2s),热流密度q范围:37~2 000kW/m2,主流焓值hb范围:93~3 176kJ/kg。
2 宽范围换热关联
2.1 关联形式讨论
对于超临界压力下流体传热问题,考虑流体在拟临界附近区域物性剧烈变化对传热造成的影响,大部分关联式在常物性关联的基础上乘以某种形式的修正函数。Jackson总结了超临界压力流体的换热关联式对常物性关联的修正方法[23],总体可分为两类:第一类是引入壁温与主流温度下的物性比以进行修正;第二类则采用适当选取关联式中无量纲准则数定性温度的方法。其中,第二类方法由于在宽广工况的参数变化条件下很难选取合适的定性温度,因而不易于广泛应用。此外,也有关联式采用两种方法组合的方式进行修正。到目前为止,已有的大多数经验关联式都是基于某些实验的有限数据建立的,故适用范围有一定局限。
对于关联形式,一方面,本文仍考虑对常物性关联采用物性比形式的修正方法,用如下形式表征径向热物性变化:

式(3)中四组物性比依次为导热比、动力黏性比、密度比、比热容比,下标w、b分别表示以壁温Tw、主流温度Tb为定性温度。
另一方面,考虑到加热过程中热物性(特别是密度)在空间上大梯度的变化,由此带来的浮力作用影响超临界水在径向的速度场分布,还应在关联式中引入以反映浮力作用对传热模型的影响[23]。以文献[8]的一组实验数据为例(如图1所示),Gr*与换热系数的趋势高度相关,即超临界水在竖直上升管中的传热模型与浮力有密切联系。所以,在关联式中引入Gr*。

图1 换热系数HTC和Gr*随主流焓值的变化Fig.1 Variation of HTC and Gr* with bulk enthalpy
同时,考虑由加热引起的密度空间变化导致主流速度的改变,即所谓热加速效应。为此,McEligot提出了无量纲数q+[24]:

浮力作用和热加速效应等因素导致加热管内的流动不同于常规流动,从而进一步影响对流传热。在仅考虑相关无量纲数低阶的相互影响的前提下,得到第二个修正系数:


图2 换热系数和q+随主流焓值的变化Fig.2 Variation of HTC and q+ with bulk enthalpy
综合以上两个方面,本文以Dittus-Boelter型关联式为基础,采用物性比修正系数f1以反映超临界压力下流体径向物性变化因素的影响(特别是在拟临界点附近);同时,考虑浮力作用、热加速效应等对流动产生影响,进而影响传热,故引入相应的修正函数f2,最终得到关联形式:

显然,这些无量纲数对Nu的影响程度各不相同,是否应全部包含在最终关联式中,仍需结合本文数据库进行检验。这主要需要考虑两个方面:
(1)各无量纲数对换热关联式的敏感性:如果某个无量纲数对Nu的影响很小,说明它不是主要影响因素,则可忽略;否则应予以保留。
(2)各无量纲数之间的相关性:若某些无量纲数间存在高度相关,则需要进一步数学处理以去除高度相关带来的信息冗余。
2.2 无量纲数的敏感性
为考察各无量纲数对Nu的贡献,即各无量纲数对Nu的敏感性,考虑采用各无量纲数的标准回归系数(SRC)对敏感性进行初步判断。由于各区域内无量纲数的影响各不相同,故将整个焓值范围大致划分为“<1 700kJ/kg”(低焓值范围)、“1 700~2 400kJ/kg”(中间焓值范围)、“>2 400kJ/kg”(高焓值范围)3个区域以方便比较。以导热比、密度比为例,从基于整个数据库得到的SRC看(见图3),这两个无量纲数并不敏感;但在低焓值范围,它们的敏感性较强。可见,这两个物性比无量纲数在不同焓值区域,对Nu的影响与作用趋势不同。

图3 无量纲数对Nu的标准回归系数(SRC)Fig.3 Standardized regression coefficients(SRC)of dimensionless numbers vs.Nu
注意到SRC一定程度上反映的是各无量纲数对传热敏感性的“线性”趋势,只能粗略反映各无量纲数的敏感性,可能存在一定偏差。而超临界传热中Nu与各无量纲数之间的关系具有强烈的非线性特征,故为进一步确认各无量纲数的敏感性,还需做更深入的敏感性分析。为此,定义平均相对误差、平均相对绝对值误差和标准偏差这三个统计指标:

其中n是实验数据点数目,e是预测值与实验值的相对误差。
具体分析方法如下:第一步,以式(5)的形式,结合收集的实验数据进行回归;第二步,取其中一项指数为0,即在关联式中舍去该项;第三步,比较新关联式与原关联式的相应三个误差指标,若各指标σ1、σ2及σ3的相对差异均在1%以内,则说明该项对关联式的预测误差影响不大,可以舍去;反之,则说明该项对预测误差有一定影响,应保留。从各无量纲数相对Nu的敏感性来看,修正项中应保留全部变量,即:

2.3 无量纲数的相关性——多重共线性
由上述敏感性分析可知,引入的各无量纲数均对换热系数有显著影响,说明各无量纲数都反映了各自“独特”的信息,对Nu有较显著贡献。但是,若无量纲数之间存在高度相关的关系,则说明它们之间又存在某种信息冗余。由于式(5)的关联方法是取各无量纲数对数形式进行多元线性回归,所以当这个线性回归模型中的无量纲数之间存在精确相关关系或高度相关关系时,就会导致模型估计失真或难以估计准确,这就是所谓的“多重共线性”[25]。以文献[8]一组实验数据中的导热比与密度比为对照,从图4可以直观看到无量纲数间一定的线性相关。

图4 导热比与密度比的相关性Fig.4 Correlation between ln(λw/λb)and ln(ρw/ρb)
为此,引入方差膨胀因子(VIF)对各无量纲数(对数形式)进行多重共线性检验。(VIFj=,其中是一个自变量与其他自变量之间的复相关系数。)一般认为[26],VIF>5就表明存在多重共线性。由表1可以看到,除lnq+可作为独立成分参与回归外,其余无量纲数均存在一定程度的多重共线性。因此,为避免模型估计失真,在建立模型、回归得到关联式之前必须消除回归变量间的多重共线性。

表1 无量纲数方差膨胀因子(VIF)列表Table1 Variance inflation factors of the dimensionless numbers
为解决这一问题,引入“主成分分析”方法:把各无量纲变量之间互相关联的复杂关系通过对自变量做线性组合的方法进行简化分析,将多个实际变量转换为少数不相关的综合指标,进而达到消除多重共线性的目的。
2.4 宽范围换热关联式
根据关于关联形式和关联变量的讨论,分别得到以整个数据库为回归数据源的全范围形式关联式和以各区域数据为回归数据源的分段函数形式关联式。
(1)全范围形式关联式
对存在多重共线性的无量纲数用主成分分析去除“信息冗余”的影响,得到的各主成分形式如下:

其中x0是常数,xi(i=1,2,…,6)分别对应为各无量纲数的系数。
计算得到用于回归关联式的各主成分见表2。

表2 主成分列表Table2 The list of principal components

关联式(9)计算结果与数据库中的实验点比较,偏差在±30%范围内的数据量占总数据的89.5%,如图5所示。关联式(9)的误差指标σ1、σ2、σ3,分 别 为 0.050 5,0.144 1,0.208 6。可见,整体预测误差较小。
(2)分段函数形式关联式
由于在拟临界点前后流体的物性参数有较大变化,拟临界点前后传热规律与趋势有较明显差异,这就解释了基于整个数据库建立的关联式(9)在中间焓值区域的预测趋势与低焓值区相比明显偏低(如图6所示)的原因。因此,为得到更具针对性的关联式,进行分区域关联。

图5 式(9)预测值(Nupred)与实验值(Nuexp)比较Fig.5 Comparison of experimental Nu numberswith those predicted by formula(9)
Zahlan[27]根据不同压力下CP随温度的变化幅度(见图7),以温度形式给出了超临界水的高密度区域、拟临界附近区域、低密度区域3个分区。本文采用该方法的焓值表达形式进行分区:

定义高密度区域(hW,hb<hpc-Δh1)、拟临界附近区域(hpc-Δh1<hW,hb<hpc+Δh2),低密度区域(hW,hb>hpc+Δh2)3个区域。本文数据库中分布于3个区域的数据量分别占总数据量的23.8%,54.0%,22.3%。
以文献[13]的一组实验数据为例,验证该分区方法的适用性(见图8)。选定工况下换热系数、比热的相关趋势变化与区域划分结果较吻合。

图6 在不同焓值范围内,全范围关联式预测值与实验值的比较Fig.6 Comparison of experimental Nu numbers with those predicted by formula(9)within different enthalpy regions

图7 不同压力下CP随温度的变化Fig.7 CPvariation with bulk temperature under different pressures

图8 焓值分区适用性验证Fig.8 Verification of the enthalpy region classification
基于上述3个区域的实验数据,分别按与式(9)同样的回归方式进行关联,最终得出分段函数形式的关联式如下:

与现有数据库的实验值进行比较,采用关联式(12),95.9%的计算结果与实验点的偏差在±30%范围内,如图9所示。关联式(12)的3 个 误 差 指 标σ1、σ2、σ3分 别 为 0.013 2,0.100 7,0.142 4。从图10的示例和表3的统计结果可以看到,通过分区域关联,式(12)与式(9)相比,拟临界附近区域和低密度区域的预测结果有了更明显的改善。然而,关联式(12)形式比式(9)复杂一些。

图9 式(12)预测值(Nupred)与实验值(Nuexp)比较Fig.9 Comparison of experimental Nu numbers with those predicted by formula(12)
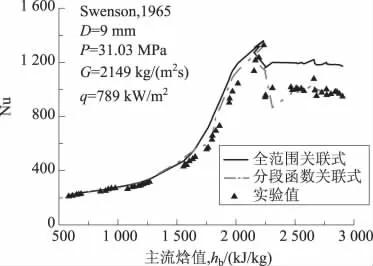
图10 式(9)与式(12)的预测结果比较Fig.10 Comparison of predicted Nu numbers of formulae(9)and(12)

表3 式(9)与式(12)预测误差大于±30%的数据量统计Table3 Statistics on the quantity of predicted data of formulate(9)and(12)whose error>±30%
3 关联式评价与讨论
为评价本文得到的关联式(9)、式(12),以现有数据库为基础,对式(9)、式(12)和部分已有关联式在预测误差带、误差值和适用范围等方面进行比较。
从表4中可以看到式(9)、式(12)在预测误差带的评价上均有较大优势。其中式(12)对局部准确度的改善效果尤其突出。
从表5的误差分析中σ1的正负可以看出,除Kuang关联式外,其余关联式的预测值普遍高于实验值;从表5中σ2,σ3的评价结果可以看到,式(9)、式(12)具有明显预测优势,与误差最大的关联式误差相差1个量级。
通过对比表6中针对3个区域的误差结果与表5针对整个数据库的误差结果可以看到:Griem、Yamagata关联式更适用于低密度区域;Swenson、胡志宏、徐峰关联式更适用于高密度区域;Jackson、Petukhov、周强泰、Kuang、式(9)、式(12)关联式在3个区域的误差水平没有发生剧烈变化,说明这些关联式适用范围较广,总体来说,又以式(9)、式(12)的计算结果为最佳。

表4 各误差带内不同关联式预测的数据量及数据量百分比比较Table4 Percentage of calculated-experimental Nu that drops in certain error bands

表5 不同关联式相对实验数据库全部数据的预测误差比较Table5 Prediction errors of various correlations relative to the whole data in the data bank

表6 不同关联式分别在3个区域内的预测误差比较Table6 Prediction errors of various correlations in three different regions
进一步,为考察本文关联式对正常传热和传热恶化两种典型工况的预测效果,分别以文献[4]的一组正常传热实验数据与文献[22]的一组传热恶化实验数据对各关联式的预测进行比较(见图11、图12)。

图11 不同关联式对正常传热的预测比较Fig.11 Comparison of experimental data with predictions by different correlations for a normal heat transfer case

图12 不同关联式对传热恶化工况的预测比较Fig.12 Comparison of experimental data with predictions by different correlations for a deteriorated heat transfer case
从图11,图12来看:(1)在高密度区域,除Griem关联式外,大部分关联式能够预测出Nu的趋势,但越靠近拟临界附近区域,各关联式的准确度差异越明显,大部分关联式的准确度开始下降,而式(9)、式(12)预测较准确;(2)在拟临界附近区域,大部分关联式能够预测出Nu的趋势,但准确度不高,有的甚至对传热恶化工况预测失效,但式(9)、式(12)不仅得到了比较符合的预测结果(尤以式(12)预测为最佳),还成功预测了传热恶化;(3)在低密度区域,大部分关联式对实验值的预测偏差有随焓值增加逐渐减小的趋势,式(9)、式(12)则预测良好,但随着焓值的升高,准确度略有下降。
4 结论
本文在广泛搜集实验数据的基础上,建立并整理了超临界压力水在竖直上升加热管中的宽范围传热实验数据库,得到如下结论:
(1)在数据库基础上采用SRC和误差比较相结合的方式讨论了各无量纲数对Nu的敏感性,引入主成分分析的方法解决了关联式回归时的多重共线性问题,由此建立了竖直上升管内超临界压力水的全范围形式和分段函数形式的对流换热关联式。
(2)与其他关联式相比,本文给出的两组关联式不仅实现了比其他关联式更准确的、更宽范围的预测,而且较好地预测了数据库中传热恶化的趋势和Nu值,其中分段函数形式关联式在恶化附近的预测更准确。
(3)总的来看,本文的全范围形式关联式预测良好;分段函数形式关联式的预测精度更高,但形式稍复杂。
[1]Griem H.A New Procedure for the Prediction of Forced Convection Heat Transfer at Near and Supercritical Pressure[J].Heat and Mass Transfer,1996,31:301-305.
[2]Jackson J D,A F J.Forced Convection Data for Supercritical Pressure Fluids.In HTFS 21540[C],1975.
[3]Petukhov B, Kurganov V, Ankudinov V. Heat Transfer and Flow Resistance in the Turbulent Pipe Flow of a Fluid with Near-critical State Parameters[J].Teplofizika Vysokikh Temperatur,1983,21:92-100.
[4]Swenson H,Carver J,Kakarala C.Heat Transfer to Supercritical Water in Smooth-bore Tubes[J].Journal of Heat Transfer,1965,87(4):477-484.
[5]Yamagata K, K N, Hasegawa S,et al.Forced Convection Heat Transfer to Supercritical Water Flowing in Tubes[J].Heat Mass Transfer,1972,15:2575-2593.
[6]周强泰.超临界压力水的管内强迫对流传热[J].华中科技大学学报 (自然科学版),1983,1.
[7]胡志宏.超临界和近临界压力区垂直上升及倾斜管传热特性研究[D].西安:西安交通大学,2001.
[8]徐峰.超临界压力下水在管内流动与传热特性研究[D].西安:西安交通大学,2004.
[9]Kuang B,Zhang Y,Cheng X.In A new,wide-ranged heat transfer correlation of water at supercritical pressures in vertical upward ducts,2008;2008.
[10]Ackerman J W. Pseudoboiling Heat Transfer to Supercritical Pressure Water in Smooth and Ribbed Tubes[J].Transactions of the ASME,1970,8:490-498.
[11]Shitsman M E.Impairment of the heat transmission at supercritical pressures[J].High Temperatures,1963,1(2):237-244.
[12]Shitsman M E.Temperature Conditions in Tubes at Supercritical Pressures[J]. Thermal Engineering,1968,15(5):72-77.
[13]Vikhrev Y V,Barulin Y D,Kon'kov A S.A Study of Heat Transfer in Vertical Tubes at Supercritical Pressures[J].Thermal Engineering,1967,14(9):116-119.
[14]Styrikovich M A,Margulova T K,Miropol'skii Z L.Problems in the Development of Designs of Supercritical Boilers[J].Thermal Engineering,1967,14(6):5-9.
[15]Lee R,Haller K.In Supercritical Water Heat Transfer Developments and Applications[C].In:Proceedings of 5th International Heat Trauster Conference Japan,vol.IV (B7.7),pp 335-339.
[16]Alekseev G A,V A S,Smirnov A M,et al.Study of the Thermal Conditions of the Wall of a Pipe During the Removal of Heat by Water at a Supercritical Pressure[J].Physical Power Institute.Translated from Teplofizika Vysokikh Temperatur,1976,14(4):769-774.
[17]Pis'menny E,Razumovskiy V,Maevskiy E,et al.Heat Transfer to Supercritical Water in Gaseous State or Affected by Mixed Convection in Vertical Tubes[C].The ASME Foundation,Inc.,Three Park Avenue,New York,NY 10016-5990(United States):2006.
[18]Mokry S,Pioro I,Kirillov P,et al.Supercritical-water Heat Transfer in a Vertical Bare Tube[J].Nuclear Engineering and Design,2010,240(3):568-576.
[19]Pioro I L,Duffey R B,Engineers A S o M.Heat Transfer and Hydraulic Resistance at Supercritical Pressures in Power Engineering Applications[M].ASME Press:2007.
[20]Pioro I L,P L K,Mokry S J,et al.Supercritical Water Heat Transfer in a Vertical Bare Tube:Normal,Improved and Deteriorated Regimes[J].Proceedings of ICAPP'08 2008.
[21]潘杰,杨冬,董自春,等.垂直上升光管内超临界水的传热特性试验研究[J].核动力工程,2011,32 (1):75-80.
[22]Herkenrath H,Euratom,Wärmeübergang an Wasser Bei Erzwungener Strömung Im Druckbereich Von 140 Bis 250Bar[M].EURATOM:1967.
[23]Jackson J D.Forced convection Heat Transfer to Fluids at Supercritical Pressure[J].Turbulent forced convection in channels and bundels,1978,2:563-612.
[24]McEligot D,Coon C,Perkins H.Relaminarization in Tubes[J].Int.J.Heat Mass Transfer,1970,13:431-433.
[25]何晓群.多元统计分析[M].中国人民大学出版社:2004,Vol.1.
[26]张文彤.SPSS统计分析高级教程[M].高等教育出版社:2004.
[27]Zahlan H,D C G,Tavoularis S,et al.Assessment of Supercritical Heat Transfer Prediction Methods.In The 5th Int.Sym.SCWR (ISSCWR-5)[C].Vancouver,British Columbia,Canada,2011.
