基于Pspice的交流调速系统的建模与仿真研究＊

2012-06-26郝玉福刘健花董海鹰

电气传动自动化 2012年2期

郝玉福，刘健花，董海鹰

（兰州交通大学，甘肃兰州 730070）

1 引言

随着电力电子技术、自动控制技术和计算机技术的不断发展，交流调速技术应用的日益广泛［1］。然而，交流电动机内部的电磁和机电关系比较复杂，具有高阶、非线性、强耦合的数学模型［2］，这给交流调速系统的设计分析和性能优化带来很大的困难。本文将采取理论研究与数字仿真相结合的方法进行设计研究。作为通用的电子电路计算机辅助分析和设计软件，Pspice在电子电路设计中得到了广泛应用，它可以对电子电路进行交直流分析、噪声分析、Monte Carlo统计分析、最坏情况分析等，力求所设计的电路更精确可靠。本文采用Pspice对交流调速系统的各个模块进行建模，对交流调速系统的动、静态特性及机械特性进行仿真分析。

2 交流调速系统的结构及建模

现代交流调速系统的结构如图1所示，分为不可控整流和逆变两部分。整流部分采用不可控三相整流桥将交流电转为直流电，逆变部分采用全控开关器件IGBT或集成的IPM模块构成三相桥式逆变器，通过PWM信号控制IGBT的导通和关断从而实现直流－交流的逆变。图1中的制动部分可根据交流电机的容量选配。

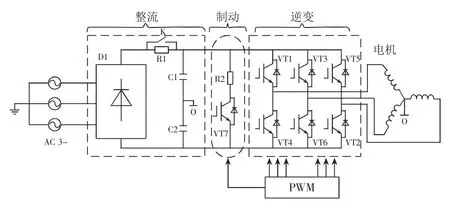
图1 交流调速系统结构图

2.1 三相不可控整流电路的仿真

图2所示为三相桥式整流电路模型。整流部分为不可控全波桥式整流，即通过6个二极管组成整流桥，根据二极管的单向导通性原理将交流电转变为直流电。三相交流电经过桥式电路整流之后输出的为脉动的直流电，在脉动直流输出的两端放置合适的电容器之后可以将脉动的直流电调理成无脉动的直流电。图3为Pspice的三相桥式整流电路仿真输出结果。图3中曲线1为未加电容器时输出的脉动直流电；曲线2为加装电容器之后输出的无脉动直流电；曲线3为输入的三相220V交流电。

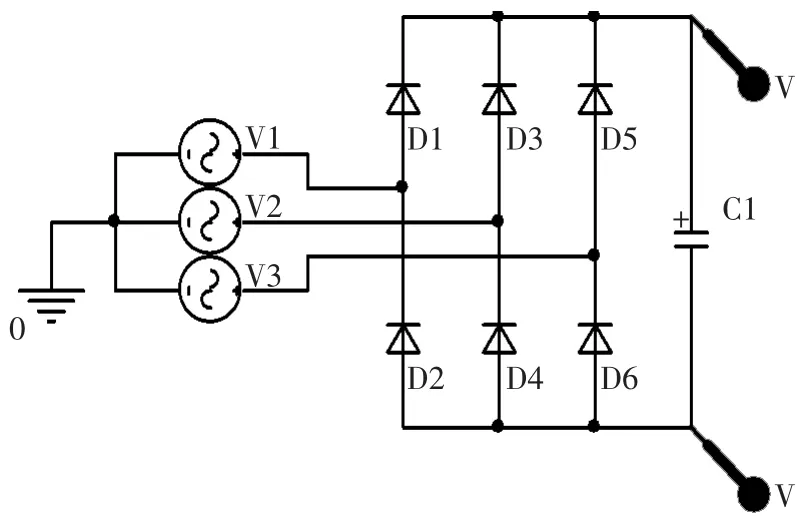
图2 三相桥式整流电路模型

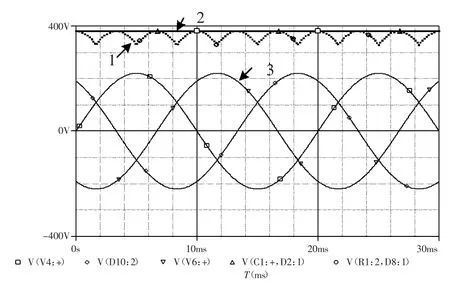
图3 三相桥式整流电路仿真结果

2.2 正弦 PWM（SPWM）的ABM 模型

正弦PWM技术在实际的工业变流器中应用非常普及。SPWM的工作原理如图4所示，图中频率为fc的等腰三角形载波与频率为f的正弦调制波相比较，两者的交点确定IGBT的通断时刻。当调制波的幅值大于载波的幅值时，PWM输出高电平（1），IGBT 导通；反之，输出低电平（0），IGBT 关断。根据SPWM的工作原理描述，通过模拟电路可以很容易实现。如图5所示，设计单独的正弦信号和三角波信号发生器，然后分别将两路信号输入到电压比较器的同相、反相输入端，即可得到所需的正弦PWM信号。但是，模拟电路实现受元器件的性能影响较大，从而导致信号的精度及可靠性不高。随着微控制器的发展，越来越多的通过软件来实现SPWM控制信号的输出，不仅可以提高精度和可靠性，还可以任意的设置信号的频率，电路结构简单。本文通过在Pspice中建立SPWM的ABM模型对其进行仿真研究。

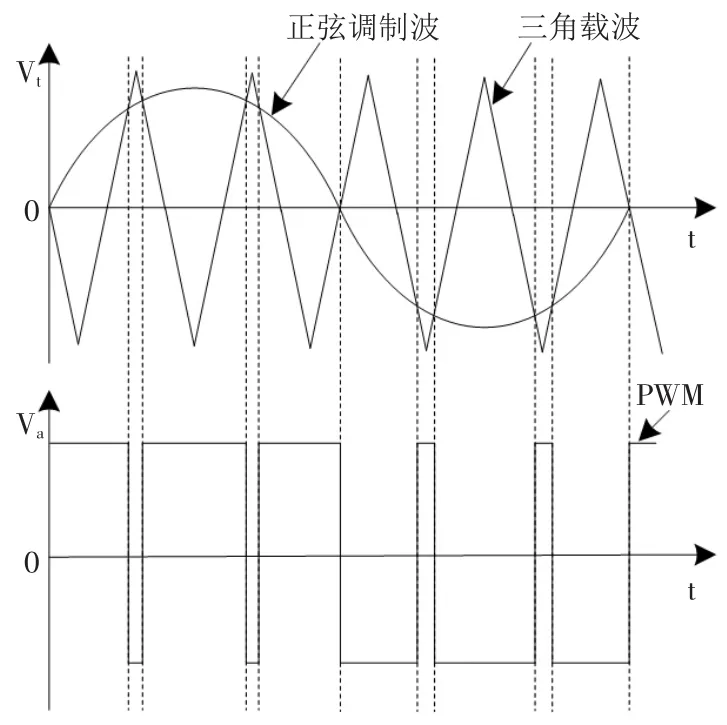
图4 SPWM的工作原理

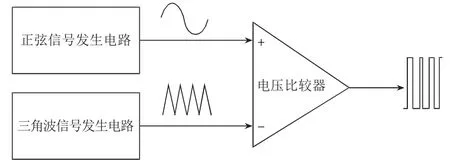
图5 SPWM信号的模拟电路实现

SPWM是正弦调制信号与三角载波信号相比较产生PWM控制信号的。对于三相逆变桥，A、B、C三相正弦调制信号幅值相同，相位互差120°，共用同一个三角载波信号。三角载波的函数表达式如式（1）［3］。式（1）中 fs为载波频率。

图6所示为SPWM的ABM模型，输出三对互补的PWM信号。图7所示为仿真结果。为了使仿真输出结果直观反应SPWM的生成过程，仿真中调制频率为50Hz、载波频率为300Hz、调制度系数Ma为 0.8。

图6 SPWM的ABM模型

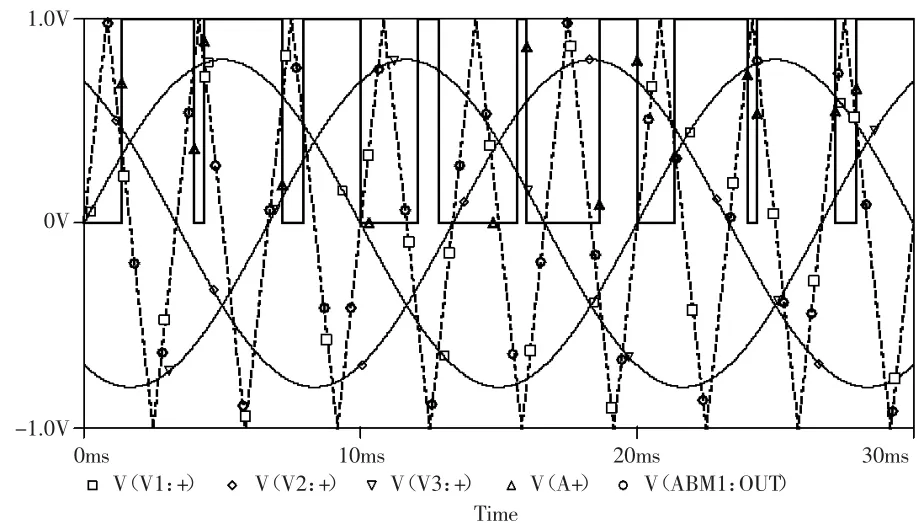
图7 SPWM的ABM模型仿真结果

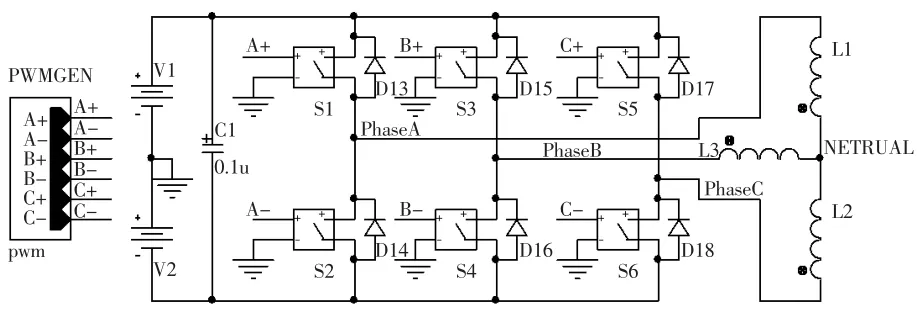
图8 PWM逆变器电路模型

图9 PWM逆变器感性负载仿真结果

2.3 三相PWM逆变器的建模

PWM逆变部分采用全控型IGBT，在仿真的过程中为了解决收敛性问题，采用理想的压控开关及续流二极管来模拟IGBT的功能。如图8所示，S1－S6为开关器件、D13－D18为续流二极管，仿真过程中逆变器的负载为Y形连接的纯感性负载。仿真结果如图9所示。曲线1为PhaseB的相电压；曲线2为PhaseB－NETRUAL的电压；曲线3为PhaseB的相电流。从电流波形可以看出，图中箭头所指的时刻电流保持不变，电流值为相电流的平均值。因为，通过控制器的AD对电机相电流进行采集的时候，可以在功率开关导通或关断后延迟一段时间进行采集，就可以采集到准确地电流值。

2.4 异步电机的建模

异步电机是一个多变量（多输入多输出）系统，而电压（电流）、频率、磁通、转速之间又互相都有影响，所以是强耦合的多变量系统。目前广泛使用的异步电机的数学模型有两种，分别是基于空间矢量理论和dq坐标变换理论。基于空间矢量理论的空间矢量电机模型公式简单、矢量图清晰；而基于dq坐标变换理论的dq电机模型无需使用复数或复变量建模时更加便于实现。两种模型对于异步电机的暂态和稳态性能分析效果一样。本文采用dq电机模型进行建模分析。通过三相电路原理推导可得到三相异步电机的数学模型，之后通过坐标变换将静止三相变换到两相dq坐标系下，就可以得到异步电机的 dq 模型。如式（2）、（3）、（4）［5］［6］所示。

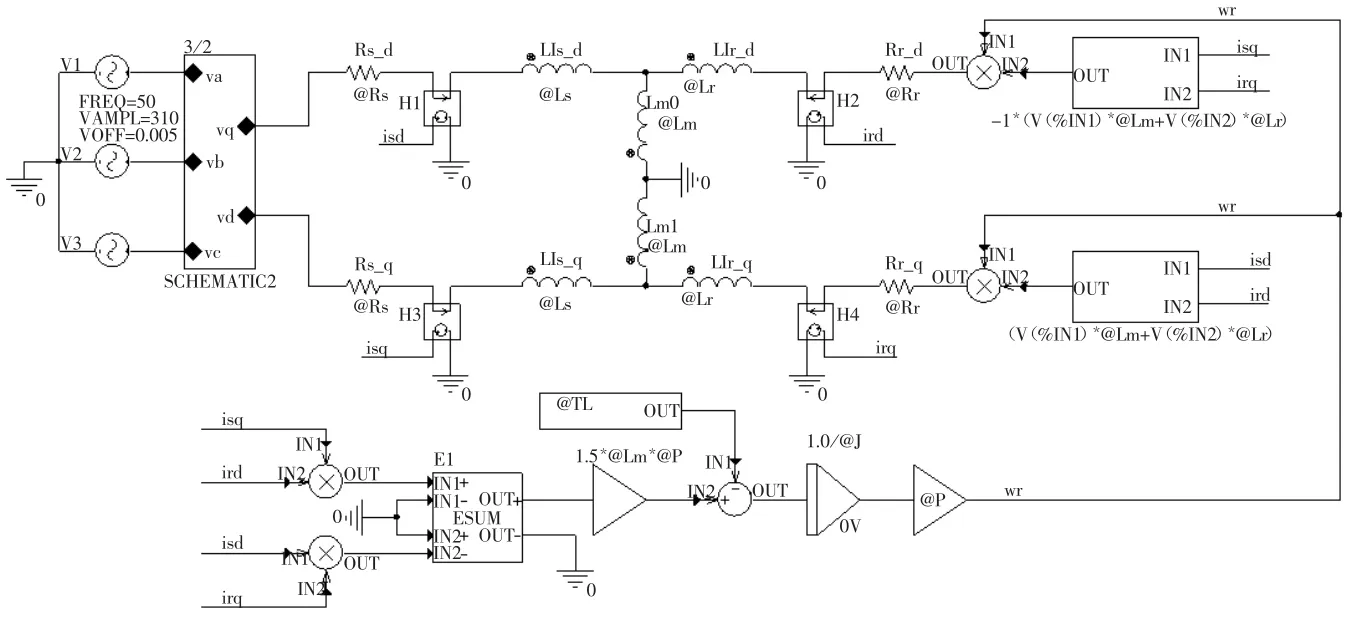
图10 任意坐标系中的异步电动机dq模型

上述表达式中，Rs、Rr分别为定子、转子电阻；ω为任意坐标系下的旋转速度；ωr为转子角速度；p为微分算子（p＝d／dt）；P 为电机的极对数。根据此模型在Pspice环境里建立异步电机的dq的电气模型及机械模型，如图10所示。图10中，3／2模块为通过ABM模型建立的三相转两相的模块［4］。

图11 仿真结果图

3 实例仿真结果

综上所述，建立好交流调速系统的各个模块，将各个模块连接起来进行统一仿真。本文以一台鼠笼异步电机作为仿真研究的对象。电机参数为：U ＝260V，f ＝50Hz，Rs ＝1.77Ω，Rr＝1.38Ω，P＝4，Lls＝16.71mH，Llr＝14.55mH，Lm＝442mH，J＝0.025kg.m2。仿真结果如图 11 所示。从图中可以看出，电机在自由加速过程中转速上升、输出转矩波动上升，达到额定转速时输出转矩接近0。0.5s时刻施加负载电流上升、输出转矩增大、转速下降。由此可知，通过该仿真能够很好的反应交流调速系统的动静态特性及机械特性。