基于有限元的场路模型在变压器直流偏磁中的应用
2012-06-23郭丽军邓秋娥
郭丽军 邓秋娥 刘 宾
(1. 机械工业信息研究院,北京 100037;2. 五凌电力有限公司,长沙 410004;3. 山东电力集团公司莱芜供电公司,山东 莱芜 271100)
三维涡流场分析一直是电磁场数值计算中研究的热门课题。国内外学者在节点元、棱边元、边界元的应用,位函数及位函数对的选择,解的唯一性及规范条件的讨论,多连域问题,内分界面条件的处理等多方面进行了深入研究,以求在计算量小、计算效率高的前提下得到的解更准确[1-2]。
关于变压器直流偏磁的计算分析,刘连光等人讨论了空间电磁场直接法与间接法的计算模型,首次提出适于均匀介质的平面波方法。通过大量的实测数据和计算论证芬兰、中国的磁暴现象对变压器乃至电网的影响,引入太阳活动和HVDC接地点变压器的模型处理及直流偏磁分析[3-4]。本文通过有限元法对变压器进行建模,分析在直流偏磁条件下,瞬态激励对场路模型的影响。
1 场路模型
1.1 磁路—电路模型
以单相双绕组变压器为例,联系其内部的电磁对偶关系与外部的电路系统,建立简化磁路模型和电路模型如图1所示。
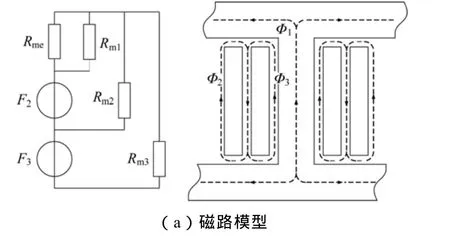
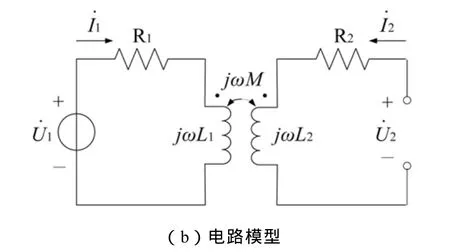
图1 单相变压器场路模型
磁路模型中Φ表示磁通,Rm表示磁阻,F为磁势。铁心中磁通为Φ1,对应磁阻Rm1;旁路磁通及漏磁通分别为Φ2、Φ3,对应磁阻为Rm2、Rm3。电路模型中L1、L2、M分别表示原、副边自感抗及互感抗,R1、R2为对应电阻。得到磁链方程矩阵形式:

ψ={ψi}为线圈磁链向量,ψ0为永磁效应磁链向量,磁链与励磁电流的关系由切割电感矩阵 LS表示,LS= [Lij], (i, j= 1,2)。
考虑电路模型端口特性:
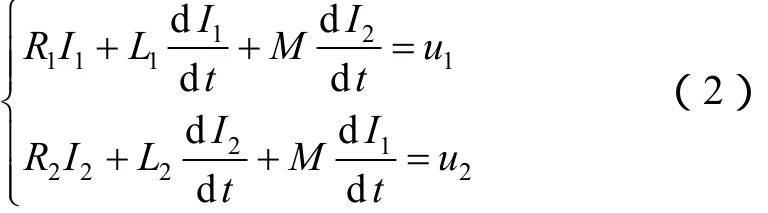
绕组电压U= dψ/dt,结合式(1)、式(2)推导电磁系统的瞬态响应方程:
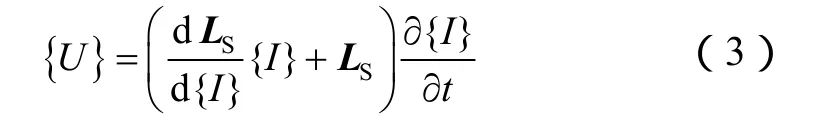
在正弦交流下, B、Φ、Rm均具有周期性。于是可FFT分解为三角函数的形式:
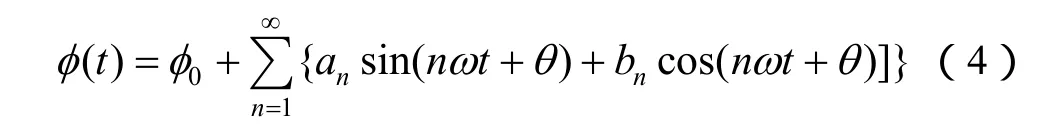
1.2 Whitney FEM
在线圈电流激励下,矢量有限元方法可根据麦克斯韦方程得到非线性磁场方程:

Whitney FEM采用棱边单元的矢量磁位函数A,单元插值公式为
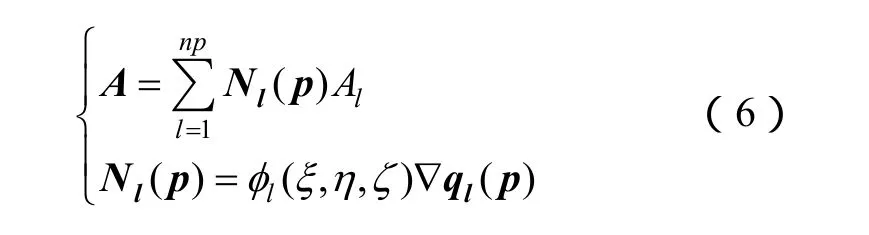
式中,Al为矢量A沿棱边l的环量,l亦表示基函数项数,Nl为与棱边对应的矢量形状函数,p = xi+ yj+zk,为整体坐标内任意场点的位置矢量,фl为局部坐标内棱边形状函数,ql为局部坐标的棱边方向函数,可通过雅克比矩阵转化为全局坐标变量,np为基函数序列项数。
上式的离散化矩阵形式为
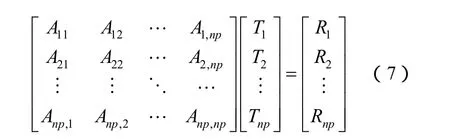
WFEM单元自由度为场矢量沿棱边的线积分,采用矢量插值函数,可直接求解场矢量。对于非均匀场计算问题,场矢量在边界单元处切向连续性自动满足,无需强制约束。
2 数值分析
选取实际单相双绕组变压器为分析对象,额定电压为10/0.4kV,额定电流13.3/573.3A,频率50Hz。具体模型如下图所示。为便于计算,选取1/8模型。
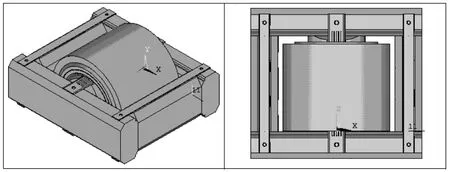
图2 变压器有限元模型
2.1 负载运行数值计算
变压器负载运行时,计算结果如图3。
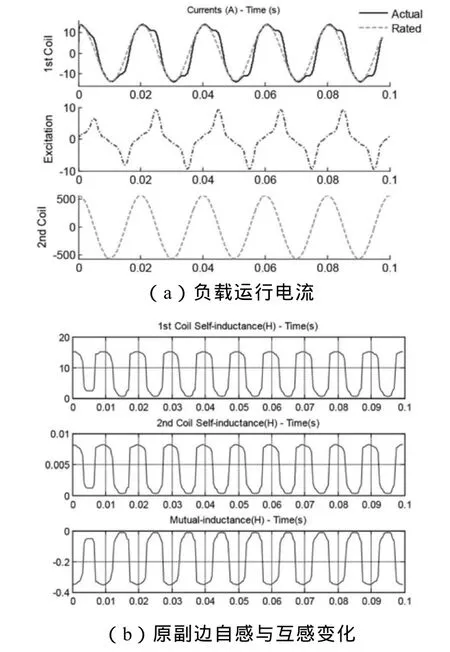
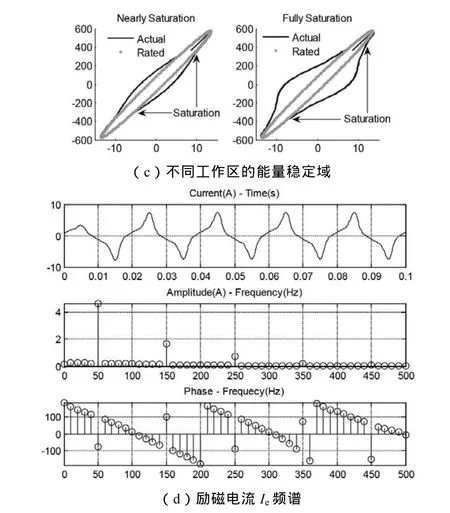
图3 负载运行数值分析
负载运行方式下铁心励磁进入饱和,一次侧绕组受励磁影响电流影响发生变化,二次绕组电流几乎不受影响。确定了分布电感变化与励磁电流的对应关系,波峰、波谷分别表示铁心工作于线性区与非线性饱和区,如图3(a)、(b)。若计及磁导非单调性,则电感波动为鞍形,而非单峰曲线。通过迭代电流表征能量计算稳定域,在非线性饱和的情况下算法仍有很好的收敛性,如图 3(c)。与额定情况时对比,发现能量域有所偏移,这是由于电磁感应出少量直流所导致另外,励磁电流的相位[-π, π]与幅值频谱分析均能反映所产生的奇次谐波,如图3(d)所示。
2.2 空载运行及直流偏磁计算
变压器空载运行时,计算结果与分析如图4所示。
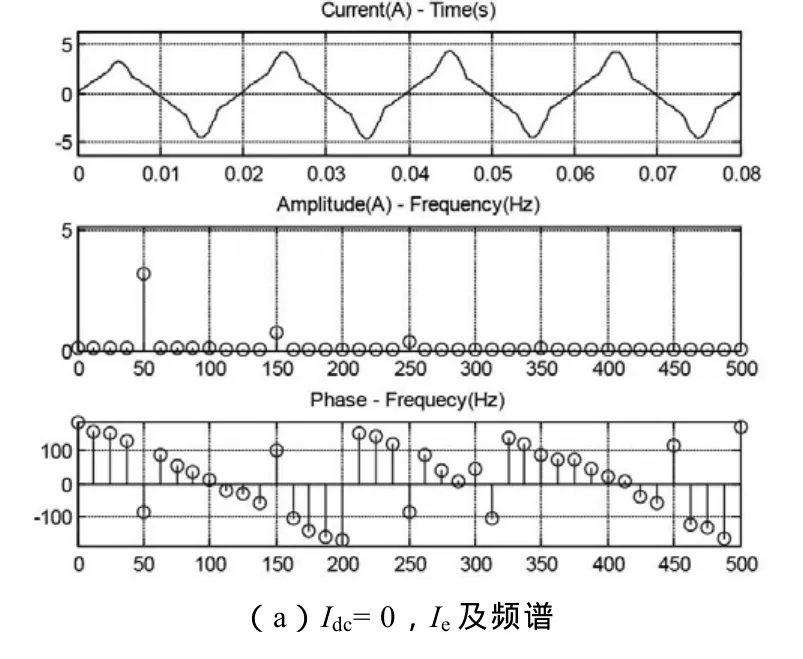

图4 空载运行及直流偏磁分析
由于 U→dψ/dt→dΦ/dt→B~H→Ie的电磁耦合关系,励磁电流为对称波,FFT频谱分解后,发现含有3、5、7次谐波,其幅值较小,且相位频谱不连续,如图 4(a)。存在直流分量时,系统受到干扰而产生衰减波动,如图4(b)所示,理论推导的励磁衰减特性得到验证。排除噪声、畸变等因素,考察衰减趋于稳定的周期信号。不同直流偏置下的励磁电流如图4(c)所示。偏磁作用下,原边电流奇次谐波分量增大,伴随出现偶次谐波分量,主要集中在6次内,并随直流分量单调递增,如图4(d)。深入研究表明,随着直流比重增大,变压器励磁饱和加剧,谐波畸变率(THD%)严重。直流扰动下能量轨迹发生明显偏移,通过频谱分析发现该现象可能与注入直流、分布参数及电磁感应情况相关,这将是动态分析的进一步工作。
5 结论
基于Whitney有限元法,利用场路模型计算变压器磁场和等效电路参数,计算结果说明该方法有效可行。分析变压器直流偏磁问题,总结场路参数受直流扰动的变化规律,为进一步分析变压器直流偏磁情况下的损耗、温升提供依据。
[1]DRAGO G, GIRDINIO P, MOLFINO P, et al. A gauged A-V-A-ψ formulation without A.n=0[J]. IEEE Transactions on Conductor Boundaries, 1994, 30(5):2976-2979.
[2]REN Z. High order differential form-based elements for the computation of electromagnetic field[J]. IEEE Transactions on Magnetics, 2000, 36(4): 1472-1478.
[3]LIU CH M, LIU L, PIRJOLA R. Geomagnetically induced currents in the high-voltage power grid in China[J]. IEEE Transactions on Power Delivery, 2010,24(4): 2368-2374.
[4]刘连光,刘春明,张冰.磁暴对我国特高压电网的影响研究[J].电网技术,2009,33(11):1-5.
[5]李晓萍,文习山.三相五柱变压器直流偏磁计算研究[J].中国电机工程学报,2010,30(1):127-131.
[6]李泓志,崔翔,卢铁兵,等.变压器直流偏磁的电路—磁路模型[J].中国电机工程学报,2010,29(27):119-125.
[7]DA LUZ V M F, LEITE J V, BENABOU A,SADOWSKI N. Three-phase transformer modeling using a vector hysteresis model and including the eddy current and the anomalous losses[J]. IEEE Transactions on Magnetics, 2010, 46(8): 3201-3204.
