三种基于支持向量机风速预测方法对比研究
2012-06-23徐蓓蓓蒋铁铮
徐蓓蓓 蒋铁铮 易 宏
(长沙理工大学电气与信息学院,长沙 410114)
风能作为一种无污染、可再生能源,已得到世界各国的高度重视[1]。目前,国内外对于风力发电各种课题的研究越来越深入,但其中关于风电场风速和功率预测的研究还达不到令人满意的程度[2]。准确预测风速可以减少电力系统运行成本,对于电网调度和资源配置有重要意义[3]。
目前,风速预测的方法主要有持续预测法、卡尔曼滤波法(Kalman filters)[3]、随机时间序列法(ARMA)[4]、人工神经网络法(ANN)[5]、模糊逻辑法(Fuzzy Logic)[6]、空间相关性法等(Spatial Correlation)[7]。人工神经网络法曾一度成为预测领域的研究热点,但也存在着许多至今无法解决的问题。支持向量机是一种基于结构风险最小化原理的预测模型,其泛化能力要好于神经网络和自回归模型,近些年来也被一些专家学者用于风速预测[8]。最小二乘支持向量机、遗传最小二乘支持向量机和经验模式分解结合最小二乘支持向量机三种方法是支持向量机模型的优化延伸。
1 建立模型的原理和方法
1.1 最小二乘支持向量机[9-10]
最小二乘支持向量机(LS_SVM)
用支持向量机(SVM)来估计回归函数的基本思想就是通过一个非线性映射,把输入空间的数据映射到一个高维特征空间中去,然后在此特征空间做线性回归。SVM 模型采用结构风险最小化准则,不仅使样本训练误差最小化,而且缩小了模型泛化误差的上界,从而提高了模型的泛化能力。通过将求解的机器学习问题转化为二次规划问题,SVM 可以得到惟一的全局最优解[4]。最小二乘支持向量机(LS-SVM)是标准支持向量机的一种扩展,它是支持向量机在二次损失函数下的一种形式。最小二乘支持向量机只求解线性方程,其求解速度快,在函数估计和逼近中得到了广泛的应用。算法的具体过程见文献[9-10],最后得到的用于函数回归估计的最小二乘支持向量机为
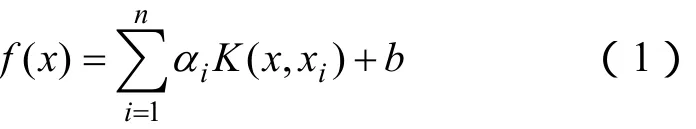
式中,K(xi,xj)称为核函数,K(xi,xj)=φ(xi)φ(xj),即等于2个向量xi和xj在其特征空间φ(xi)和φ(xj)的内积。
常用的核函数有多项式核函数、(RBF)径向基核函数和 Sigmoid核函数。本文选择径向基核函数,原因是该核函数的应用范围是最广的,且它直观反映了两个数的距离,其表达式为
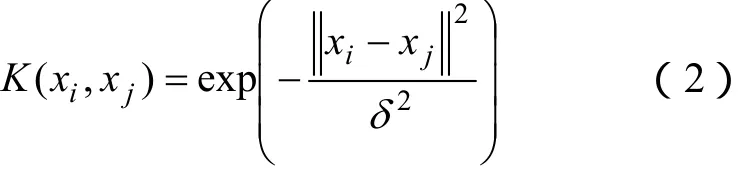
1.2 遗传算法(GA)[11-12]
遗传算法是由美国密执安(Michigan)大学J.H.Holland教授在1975提出的,是一种建立在自然选择原理和自然遗传机制上的迭代式自适应概率性搜索方法。它模拟生物进化的步骤,将繁殖、变异、杂交、选择和竞争等概念引入到算法中。该方法克服了传统优化方法较易陷入局部极值的弱点,是一种全局优化算法,其基本步骤如下:
步骤 1:设置算法的初始种群规模、最大遗传代数、交叉概率、变异概率等初始值;
步骤 2:对染色体进行编码,随机产生初始种群。本文采用实数编码;
步骤3:计算群体中每个个体的适应度函数值;
步骤 4:应用选择、交叉和变异算子产生新一代群体;
步骤 5:判断是否符合停止准则,如果满足,则执行下一步,否则返回步骤2,继续计算;
步骤 6:把当前代中出现的最好个体指定为计算结果,这个结果就是原优化问题的最优解。
1.3 经验模式分解[13-14]
经验模式分解法(empirical mode decomposition EMD)是美籍华人Huang提出的一种适用于非平稳信号的信号处理方法。从本质上讲,经验模式分解法是对时间序列进行平稳化处理,其结果是将信号中不同尺度的波动或趋势逐级分解开来,产生一系列具有不同特征尺度的数据序列,每一个序列称为一个本征模式函数(intrinsic mode function,IMF),最低频率的IMF分量通常情况下代表原始信号的趋势或均值。
经验模式分解的过程主要如下:
1)对任一给定信号x(t),确定其所有极值点,利用三次样条函数分别把他们拟合为该信号的上下包络线,计算出两包络线的均值,进而求出待分解信号和均值的差值h。
2)若h不满足IMF的要求,则重复上述过程若干次,直到得新的h满足IMF的条件;若h满足IMF的要求,则令h为原信号的第1个IMF,并求出原信号与该IMF的差值r。
3)将r作为待分解信号,重复以上过程,直到剩余信号rn满足预先给定的终止准则,则终止整个分解过程。经验模式分解的最终结果可以表示为
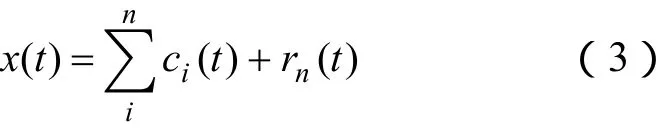
式中,ci(t)为第i个IMF分量,代表了原始信号x(t)中不同特征尺度的信号分量;rn为剩余分量,反映了原始信号x(t)的变化趋势。
2 模型建立
2.1 最小二乘支持向量机模型(LS-SVM)
对于给定的风速时间序列{X(t), t=1,2,···,n} ,支持向量机在选择输入输出变量前需对数据序列进行相空间重构,即将时间序列组转化为矩阵来寻找数据间的关系。假设t时刻的风速X(t)可由(t-1,t-2,···,t-m)时刻的历史风速值X(t-1),X(t-2),···,X (t-m)进行预测,则预测模型可表示为
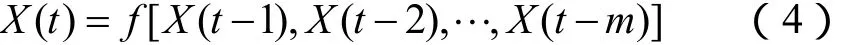
式中,m为嵌入维数。m的确定采用以均方根误差最小化为原则的增长法。
由式(3)可以构造出一个多输入单输出的最小二乘支持向量机预测模型。根据以上方法建立最小二乘支持向量机模型训练样本的输入和输出矩阵。采用LS-SVMlab工具箱1.5b版编程,用数据滚动的方法对模型进行训练和预测,即将当下预测的风速数据值视为已知数据滚入训练样本集,于此同时将距离目前时间最远的数据删除,并重新对网络进行训练,对下一个小时的风速数据进行预测,以此类推,直到完成全部的风速预测。
2.2 遗传最小二乘支持向量机模型(GA-LS-SVM)
利用遗传算法优化选择最小二乘支持向量机参数的算法具体流程如图1所示。
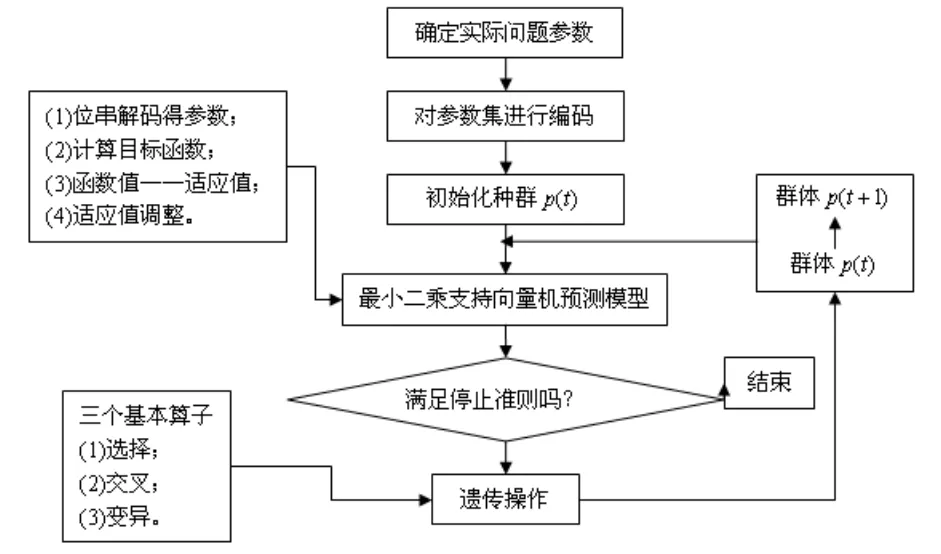
图1 遗传最小二乘支持向量机算法步骤
2.3 经验模式分解结合遗传最小二乘支持向量机模型(EMD-GA-LSSVM)
由于EMD技术在非平稳数据处理中的突出优势,将EMD与GA-LSSVM做结合,对风电场风速进行预测,起模型预测步骤如下:
1)将风速时间序列进行经验模式分解,将非平稳性时间序列分解成不同频带的高频和低频平稳时间序列。
2)建立相应的高频和低频时间序列GA-LSSVM预测模型。
3)将不同频带预测值等权求和集成得到最终预测结果。
3 模型预测
3.1 数据分析
原始数据为我国内蒙古某风电场的小时风速序列,共采用了3组数据,分别对未来24h、50h和120h风速数据进行预测。第一组数据为120个,前96个数据用于建模和训练,后24数据用于预测结果分析;第二组数据为410个,前360个数据用于建模和训练,后50个数据用于预测结果分析;第三组数据为600个,前480个数据用于建模和训练,后120个数据用于预测结果分析。为了提高最小二乘支持向量机的泛化能力,对数据进行归一化处理,使数据归一到[0,1]区间。
3.2 模型预测
将三组数据分别代入3种预测模型,24h预测结果如图1所示,50h预测结果如图二所示,120h预测结果如图3所示。
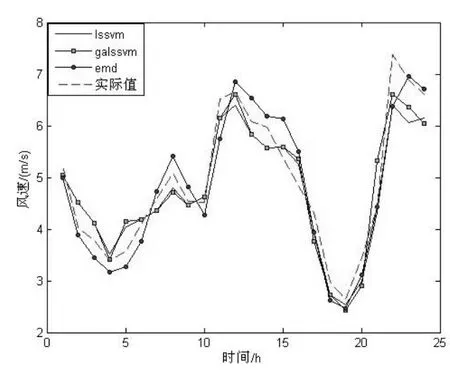
图1 24h预测结果

图2 50h预测结果

图3 120h预测结果
4 预测结果分析
为了评价模型的预测性能,采用以下统计量对模型的预测结果进行评估。
平均绝对百分比误差(MAPE):
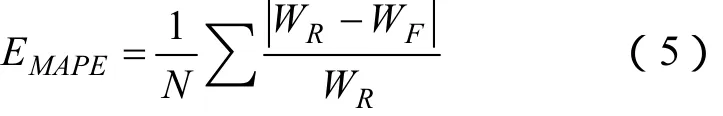
式中,WR为实际风速;WF为预测风速;N为样本数。
3种方法对 3个不同时间段的预测结果平均误差百分比情况如表1所示。由预测结果可知,对于较短的时间周期 24h的预测,3种方法的预测误差差别并不大,直接使用 LSSVM模型也能得到较好的预测结果,遗传算法并没有体现出其优势,那是因为 LSSVM对于小样本的参数选择有着较高的精度。结合 EMD后模型预测精度反而变差,这主要是由于 EMD分解一定程度上破坏了原始信号的吸引子形状,但在较长时间段的预测中表现出了明显的优势。从50h和120h的预测结果中可以看出,遗传算法对于 LSSVM参数的选择开始起到了明显的作用,样本数越大,遗传算法的优势就越明显,在对未来 120h的预测中,GALSSVM 模型的误差比LSSVM要小3.14%。同样,在样本数较大时,结合EMD的预测模型得到了更高的预测精度,而在50h的预测中达到最好的优化效果,比GALSSVM模型精度高1.93%,在120h的预测中也比GALSSVM高1.12%。由图 1,图 2,图 3可以看出,结合 EMD的预测波形与实际波形在趋势上比较相近,波形变化比较平稳,且在极值点有着较好的效果,而GALSSVM的波形在与实际波形趋势相近的同时,小范围的波动性会比较明显,也更能体现风的波动的特性。

表1 3种方法预测结果
5 结论
本文对3种基于最小二乘支持向量机的风速预测模型进行了讨论,分别用这3种方法对短、中、长3个时间段进行了预测。对于短期的预测,3种方法都有着较好的预测精度,且差别不大,对于中期和长期的预测,LSSVM模型开始体现出自身的弱点,而结合了遗传算法以及EMD的方法得到了更好的效果。在中长期的预测中,结合EMD的预测模型在预测精度上较GALSSVM模型要高,在极值点也有着较好的效果,但GALSSVM模型在小范围内的波动性更能体现风的特性,因此,不能说某个方法优于另外一个方法,而应该根据具体情况进行分析和判断,选择合适的模型种类。
[1]王晓兰,李辉.风电场输出功率年度预测中有效风速预测研究[J]. 中国电机工程学报,2010,30(8):117-122.
[2]丁明,张立军,吴义纯. 基于时间序列分析的风电场风速预测模型[J].电力系统自动化设备,2005,25(8):32-34.
[3]杨秀媛,肖洋,陈树勇.风电场风速和发电功率预测研究[J].中国电机工程学报,2005,25(11):1-5.25(11):1-5.
[4]陈树勇,戴慧珠,白晓民,等.风电场的发电可靠性模型及其应用[J].中国电机工程学报,2000,20(3):26-29.
[5]王承煦,张源.风力发电[M].北京:中国电力出版社.2003.
[6]杜颖,卢继平,李青,等.基于最小二乘支持向量机的风电场短期风速预测[J].电网技术,2008,32(15):62-66.
[7]WANG X, SIDERATOS G, HATZIARGYRIOU N, et al.Wind speed forecasting for power system operational planning[C]. Proceedings of the 8th International Conference on Probablitistic Methods Applied to Power System,2004.
[8]周同旭,基于遗传算法的支持向量机短期风速预测[J].皖西学院报,2010,26(5):106-109.
[9]张宁,许承权,薛小铃,郑宗华,基于最小二乘支持向量机的短期负荷预测模型[J].现代电子技术,2010,(18):131-133.
[10]邓乃扬,田英杰.数据挖掘中的新方法–支持向量机[M].第 2版. 北京:科学出版社,2004:25-30.
[11]王克奇,杨少春,戴天虹,白雪冰,采用遗传算法优化最小二乘支持向量机参数的方法[J].计算机应用与软件,2009,26(7):109-111.
[12]朱小梅,杨先风,张群燕.LS-SVM-GA算法在油田产量预测中的应用研究[J].煤炭技术,2010,29(11):197-198.
[13]王晓兰,李辉.基于EMD与LS-SVM的风电场短期风速预测[J]. LS-SVM 的风电场短计算机工程与设计,2010,31(10):2303-2307.
[14]刘兴杰,米增强,杨奇逊,樊小伟.一种基于 EMD 的短期风速多步预测方法[J].电工技术学报,2010,25(4): 165-170.
