基于直觉模糊推理的医学图像融合方法研究
2012-06-23赵梦旸李思彤
赵梦旸,那 彦,李思彤
(西安电子科技大学 电子工程学院,陕西 西安 710071)
直觉模糊集理论是保加利亚学者Atanassov于1983年提出,相对模糊集中仅用隶属度描述对象属于集合的程度,直觉模糊集理论创造性的提出了非隶属度的概念。该理论用一对隶属度与非隶属度来描述对象属于和不属于集合的程度,不仅描述了“亦此亦彼”的模糊概念,同时给出了对象中立,即“非此非彼”的程度,这就比模糊理论更加细腻地描述了客观对象的模糊性本质,因而具有更好的应用前景[1-3]。
针对基于传统模糊理论进行医学图像融合具有的局限性[4],文中提出了一种基于直觉模糊推理的医学图像融合新方法。将待融合图像的像素值分别用一对隶属度函数值和非隶属度函数值来表示,当两个输入像素值隶属于相同集合时,将充分考虑非隶属度对其隶属程度的影响,帮助更加全面准确的制定出直觉模糊推理规则。通过合适的推理规则得到相应的医学图像融合规则,融合得到的医学图像具有较高的质量和医学诊断价值[5-7]。
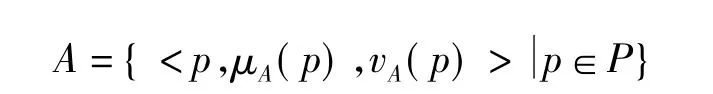
其中,0≤μA(p)≤1,0≤vA(p)≤1,分别称为直觉模糊集A的隶属度函数μA(A)和非隶属度函数vA(A),同时满足对于A上的所有p∈P,0≤μA(p)+vA(p)≤1成立。
对于直觉模糊集 A,定义 πA(p)=1-μA(p)-vA(p)为其直觉指数,用于衡量p对直觉模糊集A的犹豫程度,由上述定义可知 0≤πA(p)≤1[8-10]。
将直觉模糊理论应用于选举模型中,可使P代表某一候选人“张三”,p代表投票给该候选人的人数,则有相应的直觉模糊集A={<张三,0.7,0.2>},其中隶属度函数μA(A)=0.7表示支持张三的程度,非隶属度函数vA(A)=0.2表示反对张三的程度,直觉指数πA(p)=1-0.7-0.2=0.1表示既不支持也不反对张三的程度,即中立的程度。由此可见,IFS有效地扩展了模糊集描述客观对象的能力。
1 直觉模糊集
2 直觉模糊推理融合方法
定义1 设P是一个给定论域,则P上的一个直觉模糊集A为
2.1 图像像素点直觉模糊化
对一个命题运用直觉模糊逻辑处理,采用隶属度函数和非隶属度函数来描述其属于某个集合的模糊不确定性的程度。语言变量可以被定义为那些不能被精确划分的事件,例如,“像素点”可以被看作一个语言变量,取值可为“暗”,“一般”,“亮”,这些值可以看成是论域P=[0,1]上的直觉模糊子集标名,而每一个具体的像素值p称为基变量。将论域中的全部基变量通过隶属度函数和非隶属函数的映射,即可将图像的全部像素点直觉模糊化。
文中采用的隶属度函数为三角函数,如图1所示。将像素值论域[0,1]划分为3个直觉模糊集,分别用“暗”,“一般”,“亮”表示。文中采用语言变量、语言值、直觉模糊集和直觉模糊关系合成的方法进行推理。
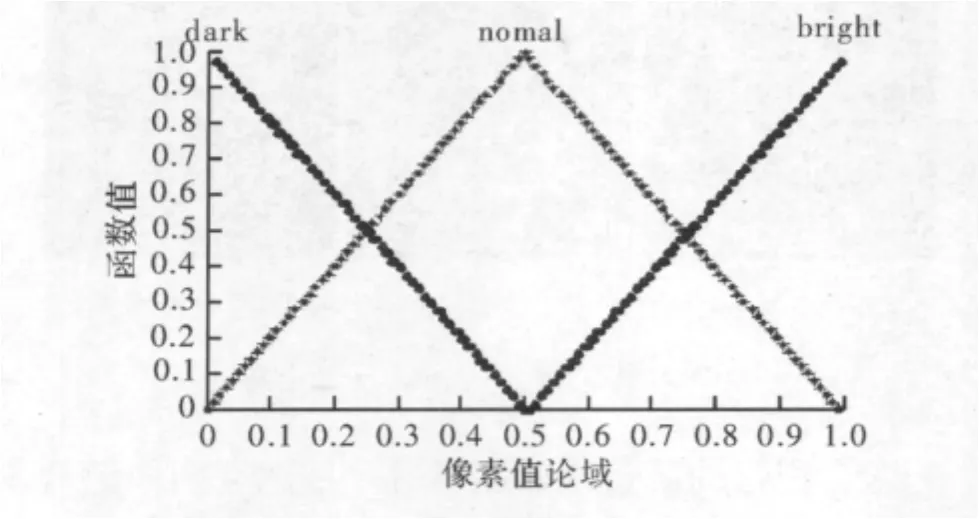
图1 三角直觉模糊隶属函数图
2.2 直觉模糊推理规则
将像素值通过隶属度函数与非隶属度函数直觉模糊化后,就得到一个从像素集P到评判集Y的直觉模糊关系R∈IFR(P×Y),即
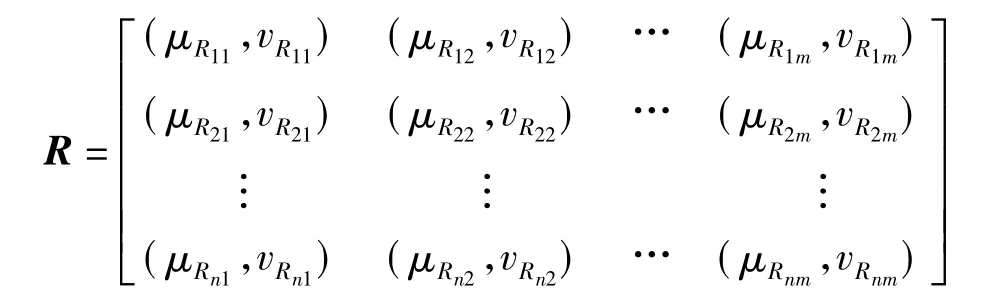
同时规定各评判因素的权重用P上的一个直觉模糊集X来表示
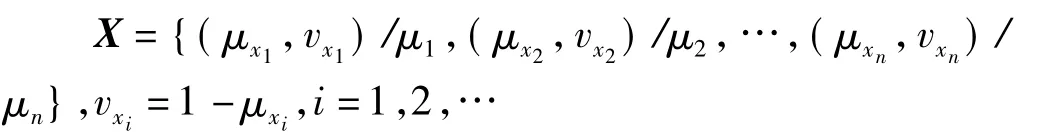
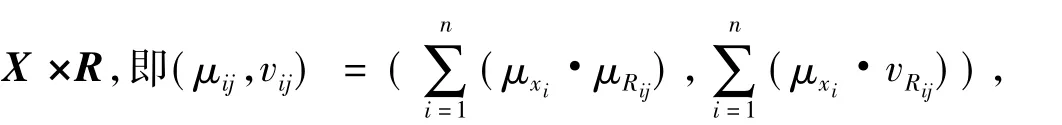
2.3 图像融合算法
文中的目的是将医学CT图像与MRI图像进行融合,得到一幅骨骼与软组织均清晰的图像。把图像的灰度区间划分为3个级别分别用“暗D”,“一般N”,“亮B”表示,其中3个灰度级别的优先级从高到低依次为:“亮”,“一般”,“暗”,高优先级的灰度可以遮盖低优先级的灰度。将上述直觉模糊推理模型中n取2,m取3,模型简化为
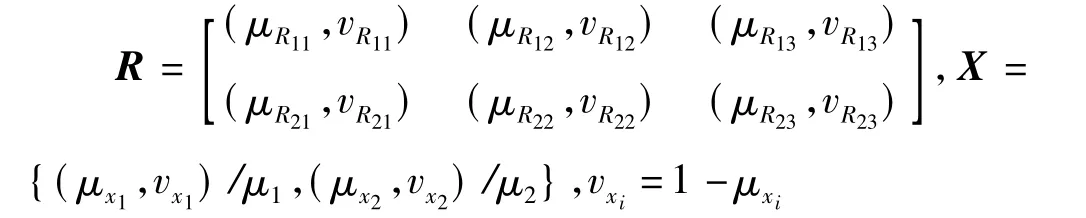
首先,将输入图像的对应像素点直觉模糊化,用矩阵R来表示。然后通过直觉模糊数排序判断出两个输入像素点的最大隶属灰度级别,直觉模糊数排序规则为:(1)在隶属度数中进行比较,得到最大的隶属度值max(μRij)。(2)判断该 max(μRij)是否大于等于与其对应的vRij,若成立则该直觉模糊数在最大的支持度下属于某级别,若不成立则该直觉模糊数在最大的质疑度下“属于”某级别,此种情况的属于我们有可能对其进行怀疑。通过排序后得到两个输入像素点在最大支持度下的灰度级别,结合灰度级别的优先级遮盖性,判断出融合图像在该对应像素点处所属的灰度级别,其共有9种可能的情况:(1)if x1∈D,x2∈D then y∈D;(2)if x1∈D,x2∈N then y∈N;(3)if x1∈D,x2∈B then y∈B;(4)if x1∈N,x2∈D then y∈N;(5)if x1∈N,x2∈N then y∈N;(6)if x1∈N,x2∈B then y∈B;(7)if x1∈B,x2∈D then y∈B;(8)if x1∈N,x2∈B then y∈B;(9)if x1∈B,x2∈B then y∈B;算法流程如图 2所示。
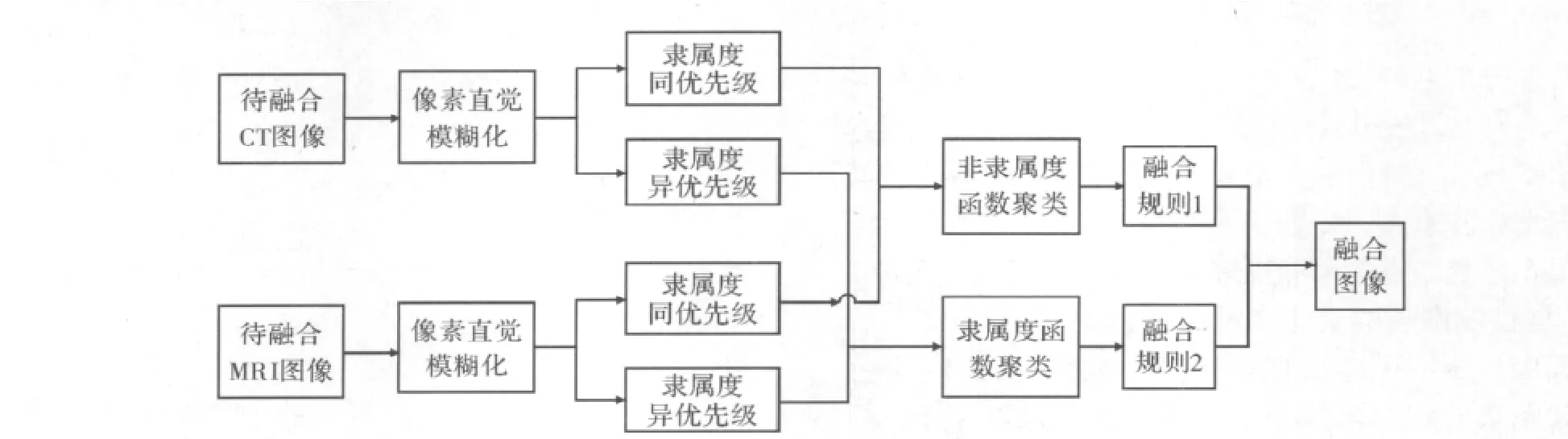
图2 直觉模糊推理图像融合算法流程图
当两个输入像素点的灰度级不同时,融合像素值所属的灰度级别总是取两个输入像素点所属灰度区间中优先级较高的一个,并令评判权重矩阵X=(1,0),1作为优先级较高的灰度区间系数,这样就可以充分保留该像素点处的有用信息。
3 仿真实验及分析
3.1 算法结果分析
文中进行的医学图像融合的实验图像为4组CT图像与MRI图像,如下所示。其中第一、二组为未经处理的源医学图像。第三组是第二组医学图像经模糊化产生的图像,它可以验证当医学图像质量下降时,文中算法依旧有效。3组待融合图像如图3~图5所示。
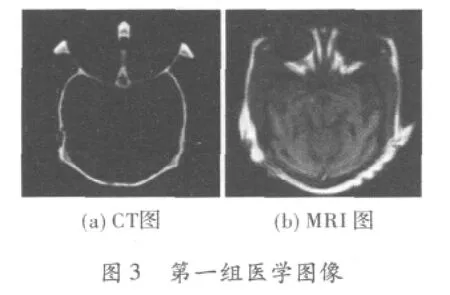
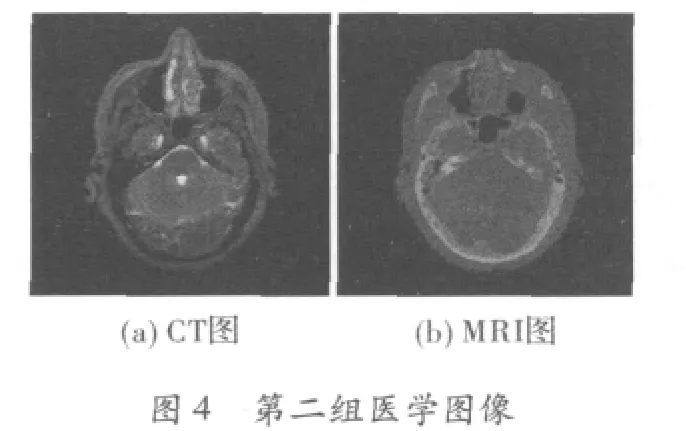
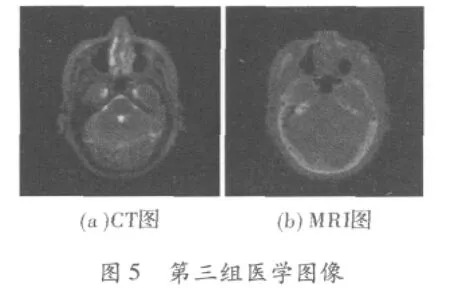
待融合的两幅图像从数据结构上来看,必须是相同分辨率的经过严格配准的图像。此处将8位灰度图像的[0,255]灰度区间映射至[0,1]的双精度区间再对其进行直觉模糊化处理,然后按照上述融合规则进行输出。图6是利用直觉模糊推理融合出的3组医学图像。
3.2 与模糊推理的对比实验结果分析
利用传统的模糊推理进行图像融合,得到的实验结果如图7所示。与基于直觉模糊推理的融合方法相比,其在图像的纹理清晰度上表现较差,大量的细节信息流失。
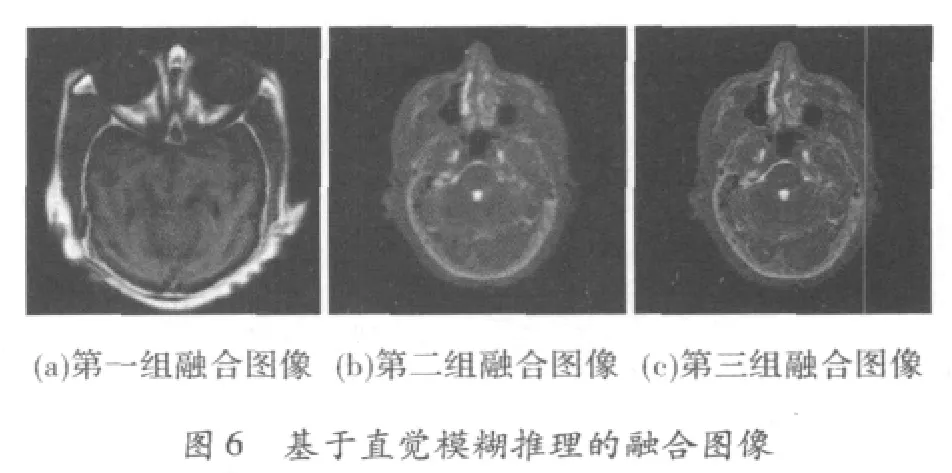
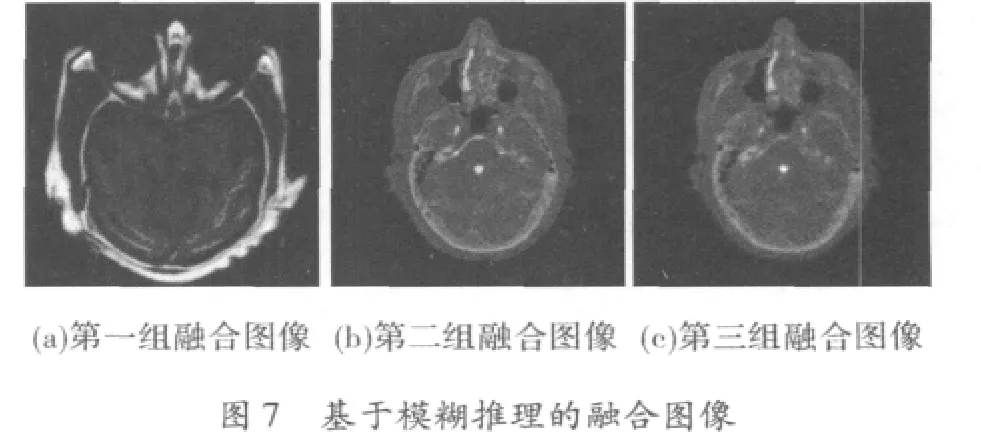
融合图像的质量还可以通过一些融合图像评价参数来进行定量评价。文中采用的指标有信息熵E和平均梯度。图像的熵值E是衡量图像信息丰富程度的一个重要指标,其值越大表示融合图像的信息量越多,融合图像所含的信息越丰富。信息熵E定义为
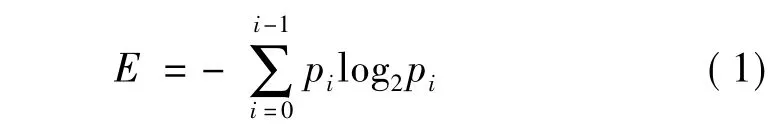
其中,pi为灰度值等于i的像素数与图像总像素数之比。平均梯度可以敏感的反应图像对微小细节反差表达的能力,一般,越大,图像层次越多,图像越清晰。平均梯度定义为
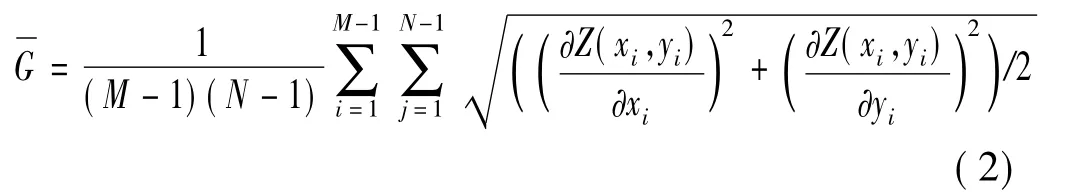
表1给出了两组医学源图像的相关融合参数,可以看到文中提出的方法评价参数明显优于基于模糊推理的图像融合方法。
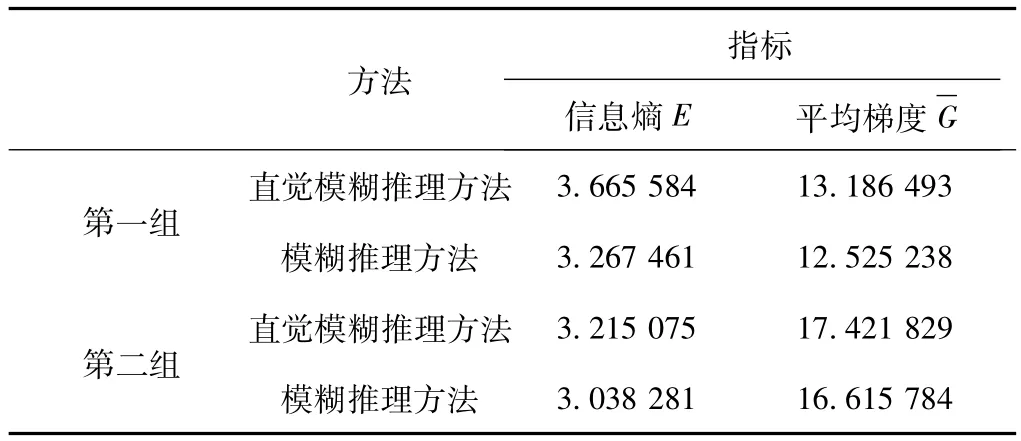
表1 两种算法的融合参数评价
4 结束语
提出了一种基于直觉模糊推理的图像融合新方法,利用直觉模糊概念更精确全面的反应客观世界本质的优势,将输入图像的像素点科学的分类分析,更细致地完善了图像融合的规则步骤。从而提高了融合图像的质量。同时,在仿真实验中通过主观判别以及平均梯度等融合效果客观评价指标比较,表明文中提出的方法效果明显优于一般的模糊推理的融合效果。
[1]TENG Jionghua,WANG Suhuan,ZHANG Jingzhou,et al.Fusion algorithm of medical images based on fuzzy logic[C].2010 Seventh International Conference on Fuzzy Systems and Knowledge Discovery,2010:546 -550.
[2]那彦,焦李成.基于多分辨分析理论的图像融合方法[M].西安:西安电子科技大学出版社,2007.
[3]宋超,雷英杰.直觉模糊集理论及其在模糊信息处理中的应用[J].电光与控制,2010,17(2):43 -45.
[4]黄伟.像素级图像融合研究[D].上海:上海交通大学,2008.
[5]刘天华.直觉模糊推理与决策的几种方法研究[D].济南:山东大学,2010.
[6]刘自新.直觉模糊规划理论研究及应用[D].大连:大连理工大学,2007.
[7]汪家旺,罗立民,舒华忠.CT、MR图像融合技术临床应用研究[J].影像技术学,2001(8):604-608.
[8]陈昊,杨俊安,黄文静.基于条件熵的直觉模糊条件推理[J].电子与信息学报,2009,31;(8):1852 -1854.
[9]孔韦韦,雷英杰.基于直觉模糊熵的红外图像预处理方法[J].系统工程理论与实践,2010,30(8):1485 -1487.
[10]LAKSHMANA G N V,VENKATESHWARI G,GEETHA S.Ranking of intuitionistic fuzzy numbers[C].2008 IEEE International Conference on Fuzzy Systems,2008:1972 -1973.
[11]张弛,雷英杰,蔡茹.基于三角模的直觉模糊综合评判模型[J].计算机工程与应用,2008;44(26):133-134.
