接收机增益选择与ADC噪声电平匹配

李立明

(西安电子工程研究所 西安 710100)

1 引言

随着模数转换 (ADC)技术的发展，ADC的采样速率迅速提高，这就为使用过采样(oversampling)技术提高信号的检测性能提供了可能。当将高性能的ADC与接收机级联时，ADC的噪声有可能会淹没掉接收机输出的小信号，从而影响接收机的灵敏度。为减少这种影响，通常采取提高接收机增益的方法。但接收机增益的提高会压缩其输出动态范围，进而影响系统的动态范围。因此，接收机与ADC的匹配就是在尽可能减少级联引起信噪比损失的前提下，来满足系统对动态范围的要求。长期以来，人们普遍认为接收机的输出噪声应该高于ADC基底噪声1～2最低有效位LSB，其实这种认识是不完全正确的，特别是在高速ADC和过采样技术出现以后，ADC电路的设计以及接收机增益的选择已与原来的设计有了很大的不同。为了揭示信号检测能力与ADC噪声之间的关系，本文从ADC噪声电平和动态范围开始，讨论过采样对噪声电平的影响，如何计算接收机灵敏度，ADC噪声对接收机系统灵敏度的影响，如何计算接收机的噪声系数，脉冲压缩对ADC噪声电平的影响，以及大信号对接收机噪声性能的影响等问题。

2 系统定义

为了便于问题的描述，将接收系统划分为前端模拟接收机和后端数字中频接收机两部分。

来自天线的微弱射频(RF)信号从图1中的A点进入模拟接收机，经模拟接收机的高放、混频、中放并将中频(IF典型值为30MHz～60MHz)送至B点，IF信号经数字中频接收机的高速ADC进行采样，经由数字匹配滤波器滤波后送至D点。

图1 接收机系统的组成框图

将图1的A点到B点的信号链定义为“模拟接收机”，B点到D点的信号链定义为“数字中频接收机”，A点开始直到D点为止定义为“接收机系统”。因为在定义接收机系统检测灵敏度时，必须指定测试点的位置，测试点位置不同，接收机系统的噪声系数及检测灵敏度会有所不同。因为匹配滤波的功能是在数字域实现的，模拟接收机的作用仅仅是信号无失真放大及传输，因此模拟接收机的带宽通常要比所要求的匹配滤波器的带宽大，因而从B点输出与从D点输出所得到的噪声系数及检测灵敏度会有很大的不同。

3 ADC的噪声电平和动态范围

ADC的噪声包含热噪声和量化噪声，ADC的噪声电平是指单独对ADC测量时热噪声和量化噪声之和。ADC的动态范围是指从ADC的噪声电平起到ADC满量程(Full-scale)的工作范围，通常用分贝(dB)表示。本文将ADC满量程对应的输入信号功率记为FS功率。一旦ADC的规格给定以后，其满量程信号功率FS即为一定。为了确定ADC的动态范围，需要知道ADC的噪声电平，它可以通过测量信号噪声比(SNR，或简称信噪比)来确定。ADC能够达到的最大信噪比由下式确定［1］:

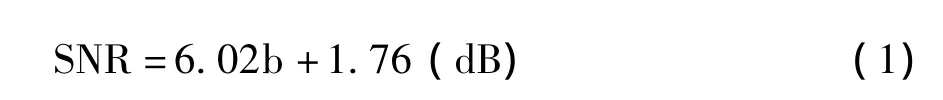
其中b是ADC的量化位数。(1)式是理想情况下(不考虑热噪声)，从ADC输出端测量时(即图1中的C点)，ADC能够达到的最大信噪比。对于12-bit的ADC而言，(1)式给出的最大信噪比SNR=74dB。然而由于热噪声的存在，ADC实际上能够达到的SNR比上式测算的SNR要小很多(对大多数商用高速ADC芯片来说，实际能够达到的SNR比上式测算的SNR平均小8dB左右)。ADC实际可达到的SNR可以通过测量给予确定。测量方法是:将ADC输入端接上匹配负载，用大量的采样值计算ADC的输出噪声功率。然后在ADC输入端施加一个功率比ADC的FS小1～2dB的正弦波，计算ADC的输出信号功率，从而得到ADC的信噪比。

ADC的信噪比通常与输入信号的频率有关，不同的输入频率测量得到的信噪比约有1～2dB的偏差。ADC的信噪比也可在器件的手册中直接查找。在器件的手册中，SNR表示为 SNR=66dB@-1dBFS，它表示当输入正弦波信号的功率比ADC的FS小1dB时，测量得到的信噪比为66dB。如果我们在一张图上画出FS线，-1dBFS线以及SNR，就可以确定出ADC噪声功率的大小。在图2中，ADC的噪声功率电平用NΔ@FS/2表示，这里NΔ是ADC的噪声总功率，FS是ADC的采样频率。图2中的其它数值将在后面逐一讨论。

通过测量或通过查阅器件手册［4］可得到ADC的SNR是输入信号功率与ADC第一Nyquist区域中噪声总功率NΔ之比。在图2中标注ADC噪声总功率时使用了“@FS/2”的记号，就是强调在FS/2频带范围内总的噪声功率。由于ADC的噪声功率均匀扩展至整个第一Nyquist区域，因而ADC的噪声功率谱密度即为:

ADC的噪声功率是由ADC的制造工艺和ADC的设计电路共同确定的数值。一旦ADC电路设计完成以后，ADC的噪声功率就确定了下来，并且是一个与采样频率无关的数值。因此当采样频率提高时，噪声功率被扩展至更宽的频率范围，因而噪声功率谱密度随采样频率的上升而下降。这就是采用过采样技术来降低ADC的有效噪声功率的主要理由。

4 过采样的处理增益

ADC噪声可以看成是白噪声。当使用不同的带宽进行滤波时，滤波器输出的噪声功率随滤波器带宽的不同而变化。在我们讨论ADC噪声对接收机系统的性能影响时我们更多关注的是模拟接收机和ADC级联处的噪声功率，因而我们需要将测试点的噪声功率等效到ADC的输入端，即图1中的B点。因此我们引入ADC有效输入噪声功率的概念，它表示可将ADC看成是一个理想无噪声器件，而将测试点的噪声等效成ADC输入端的一个可加性噪声源，以在测试点得到相同的噪声功率来确定ADC输入端可加性噪声源功率的大小。ADC可以看成是增益为1的器件，故在目前考虑的情况下，可认为ADC的输出噪声就等于其有效输入噪声。

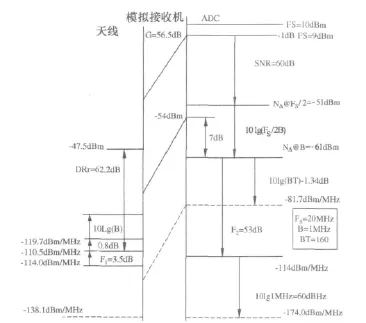
图2 接收机系统的噪声电平图示

如式(2)所示，提高ADC的采样率可以降低ADC噪声功率谱密度，使用过采样技术可以降低ADC的有效输入噪声。因为所感兴趣的频率分量被限制在信号带宽之内，因此从匹配滤波器的输出端测量ADC的噪声时，ADC自身的噪声功率从以前的NΔ下降到了NΔ2B/FS，即ADC实际能够达到的SNR增加了FS/2B倍，故将FS/2B称为过采样的处理增益，记为:

图2中将过采样增益表示为10lg(FS/2B)，ADC有效输入噪声从图中“NΔ@FS/2”一线下降到了NΔ@B一线，它也是将匹配滤波器的输出作为测试点时，ADC的有效输入噪声功率。

图2是一个实际的ADC芯片(ADS2807)［4］的检测性能曲线。可以看出在ADC之后的有效输入噪声功率为-51dBm，如果ADC之后的滤波器带宽为1MHz，而采样频率为20MHz，过处理得益为10dB，则滤波之后的有效输入噪声功率为-61dBm。这意味着在ADC输入端施加一个功率为-61dBm的正弦信号，在滤波器之后即图中的D点测量得到的SNR为0dB。将匹配滤波器的输出作为测试点时的有效输入噪声功率定义在带宽为B时的ADC的检测灵敏度Sadc，或者表示为 Sadc=-61dBm/MHz。

5 ADC的噪声系数

一个系统产生噪声的能力可以用噪声系数来衡量。噪声系数是指一个标准噪声源经过一个增益为G，端接负载且完全匹配的无噪声系统后的噪声功率，与经过一个结构完全相同，但有噪声的系统后，噪声增加的倍数。比如功率为-100dBm的噪声源经过一个增益为20dB的系统，如果是无噪声系统，则输出噪声应为-80dBm。实际上系统是要产生噪声的。假如输出噪声功率为-76dBm，那么系统的噪声系数为4dB。在噪声系数的测量中，标准噪声源通常等效成一个290K温度下1Ω电阻上所产生的噪声。根据热力学中的Nyquist定理，标准噪声源产生的噪声功率为No=KToBn，这里K是Boltzman常数，对于To=290K和Bn=1MHz，No=-114dBm，或按照功率谱密度表示为-114dBm/MHz。通常我们将带宽B用1MHz进行归一，则噪声源输出功率的通用表达式是

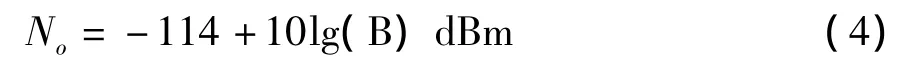
这里的B是一个无量纲的数，它表示用MHz度量的系统带宽。

对于ADC来说，因为其本身是要产生噪声的，因而也可以用噪声系数来表示ADC产生噪声的能力。因为ADC的增益为1，一个-114dBm/MHz的噪声源经过ADC后，倘若ADC不产生噪声，那么ADC的输出噪声功率在1MHz的带宽内仍然应该为-114dBm。但实际的ADC在图1中的D点产生的噪声为-61dBm/MHz，因此从D点测量时，ADC的噪声系数应为-61-(-114)=53dB。可以看出，如果我们将C点作为测试点，那么从“NΔ@FS/2”线到-114dBm/MHz线的距离即为ADC的噪声系数。

6 检测灵敏度的定义与测量

用一个纯正弦波输入到模拟接收机输入端(图1中的A点)，记录输入正弦波的功率Pi并用dBm表示。在模拟接收机输出端(图1中的B点)测量正弦波的功率Po，也用dBm表示。并将输出功率Po相对于输入功率Pi画成一条曲线，见图3。

因为在模拟接收机输出端测量的功率实际上是信号与噪声的总和，因而图3给出的曲线实际上是Po=So+Nr与Pi的曲线，这里So是模拟接收机输出的信号功率，Nr是模拟接收机输出的噪声功率。当信号很大时，噪声可以忽略，因而

当信号很大时，SNR≫1。

在这条曲线的中间段，输入输出关系为一条直线。如果接收机的增益为G(dB)，那么这条直线代表的方程为:

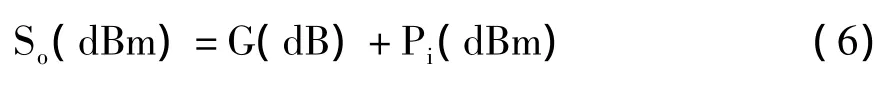
它是一条斜率为1的直线。沿着这条直线的渐近线代表输入信号功率与输出信号功率的关系曲线，如图3中虚线所示。

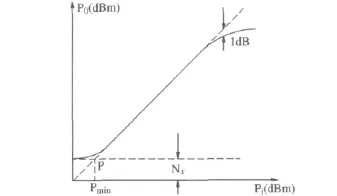
图3 检测灵敏度的定义与图示

在曲线的最底端，因为信号比噪声小很多，故信号与噪声的功率基本由噪声确定，因而

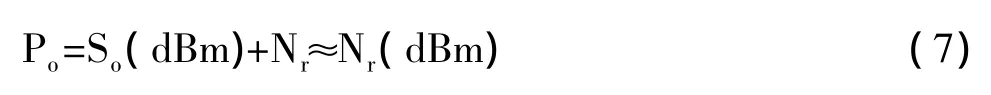
当信号很小时，SNR＜＜1。

当输入功率继续减小时，输出功率将几乎不再变化。这条底部逐渐接近水平的线段有一条渐近线，即水平渐近线，表示输入功率为0时模拟接收机的输出功率也就是模拟接收机的输出噪声功率Nr(dBm)，它与斜率为1的直线相交于P点，交点P表示信号功率与噪声功率相等，即SNR=0dB。那么P点对应的输入功率Pmin就是模拟接收机的检测灵敏度，也称为最小可检测信号功率。交点P所对应的输出功率就是输出噪声功率Nr。Nr与Pmin的差值就是接收机的增益G(dB)。

在曲线的最高端，当输入信号的功率继续增加时，由于模拟接收机中半导体器件逐渐趋于饱和，输出信号功率将逐渐偏离原来的直线而被压缩，当输出功率偏离直线1dB时的那一点称为1dB压缩点，对应的输入功率与输出功率分别被称为1dB压缩点的输入功率和1dB压缩点的输出功率。从噪声功率开始到1dB压缩点的功率范围称为模拟接收机的动态范围。

因为系统的增益是一个与信噪比SNR无关的量，因而我们在图中总是将输出功率相对于增益归一化，即输出功率表示为Po/G。

实际测量的输出功率是信号功率和噪声功率之和，Po=So+Nr，因而输出功率与噪声功率之比为:

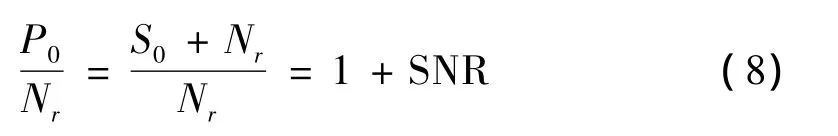
即在大信号时，SNR＞＞1，输出功率与噪声功率之比就是信号噪声比SNR。

而在小信号时(比如SNR＜5dB)，实际的SNR为输出功率与噪声功率之比减1，即:

因而小信号时，直接用输出功率与噪声功率之比来估算SNR会带来较大的误差。

7 模拟接收机与ADC的级联

在我们前面讨论ADC的噪声电平时，我们假定施加在ADC输入端的信号是一个没有噪声干扰的纯正弦信号。实际上当ADC与前端模拟接收机级联时，输入到ADC的信号通常是模拟接收机的输出信号和输出噪声的叠加。在这种情况下，我们更加关注的是级联以后信号噪声比的变化。

当模拟接收机与ADC级联时，由于ADC噪声的影响，接收机系统的检测灵敏度会有所降低，这种影响可以用接收机系统的噪声系数恶化来衡量。与此同时，由于接收机自身噪声的存在，级联又会使ADC输入端的噪声电平抬高，因而ADC的动态范围会被压缩。为了揭示两者之间的关系，我们用图4所示的简化原理图来表示模拟接收机与ADC级联时的噪声模型。

图4 ADC与接收机级联时的等效电路

我们在图4中将模拟接收机和ADC等效成是理想的、无噪声的系统，而将模拟接收机的输出噪声Nr和ADC的有效输入噪声(即ADC的检测灵敏度)NΔ用两个相互独立的可加性噪声源来表示。

当ADC未与模拟接收机级联时，模拟接收机输出的SNR为So/Nr。级联ADC后，噪声功率由原来的Nr增加到Nr+NΔ，因此SNR变为So/(Nr+NΔ)，SNR的恶化程度表示为:

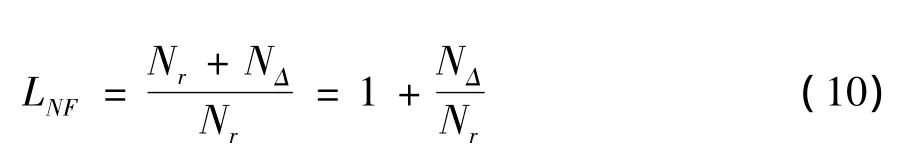
这里我们用LNF表示信噪比的损失，它同时也是噪声系数的损失。

当ADC未与模拟接收机级联时，ADC的动态范围为FS/NΔ，与模拟接收机级联后，由于模拟接收机自身的噪声，在ADC输入端总的噪声功率由原来的NΔ变为Nr+NΔ，因而ADC的动态范围被压缩到FS/(Nr+NΔ)，ADC的动态范围被压缩的程度表示为:

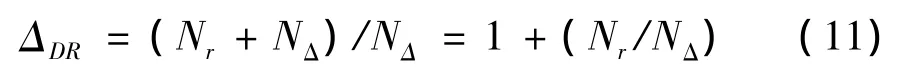
我们将模拟接收机输出噪声功率Nr与ADC有效输入噪声功率NΔ之比定义为:

那么上边的两个表示信噪比损失和和ADC动态范围的式子可以分别表示为:

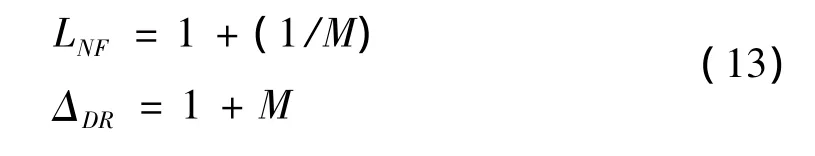
据此我们可以画出LNF以及ΔDR相对于M的曲线如图5所示。图中实线表示LNF相对于M的关系，使用左边的刻度。可以看出，LNF随M的增大而减小。图中的虚线表示ΔDR随M的变化曲线，它使用右面的纵坐标刻度。可以看出，当接收机输出噪声功率Nr等于 ADC有效输入噪声功率 NΔ时(M=1=0dB)，信噪比的损失为3dB，ADC动态压缩也为3dB。当M=7时，SNR的损失约为0.8dB，而同时ADC的动态范围的损失约为7.9dB，这是一个很好的折衷，我们将其称为“7dB准则”。

图5 信噪比损失、动态范围损失与噪声功率之比M的关系

应当指出的是，测量模拟接收机的输出噪声Nr，以及ADC的有效输入噪声 NΔ，进而求出M，然后通过式(7)来计算LNF和ΔDR的方法是不够精确的。因为在测试模拟接收机的输出噪声功率时，测量结果往往与测试设备的带宽等工作参数有关。因此当模拟接收机与测试设备相连时，实际测量得到的噪声功率并非与接收机实际输出噪声功率相一致。在LNF、ΔDR以及 M这三个量之间，只有 ΔDR是可以被准确测量的，因为它是模拟接收机与ADC级联前后在匹配滤波器输出端测量时，输出噪声增加的倍数。得到ΔDR后，就可以确定出M和LNF的数值。因此以ΔDR作为横坐标，以LNF及M作为纵坐标作图将会更为有用，按照这种思路重新作图后得到图6。如果允许的动态范围损失为7dB，那么在横坐标上找到7dB的点，垂直向上查看，当与实线(LNF)相交时，从左侧纵坐标读出的SNR损失为1dB，继续往上查看，当与虚线(M)相交时，从右侧纵坐标上读出此时需要的M值为6dB。

图6 信噪比损失与动态范围损失之间的关系

图6给出了SNR损失和动态范围DR损失之间的依存关系。所谓的ADC与接收机噪声的匹配，其主要目的在于尽可能减少级联引起的信噪比损失，又不致影响系统固有的动态范围，实际上是在SNR损失和动态范围损失之间作出一种折衷。我们可以将SNR的损失折算到接收机的输入端，并用接收机噪声系数的损失，或接收机检测灵敏度的损失来表示。以前面第4节给出的实际数值为例，说明这种折算的过程。假如我们希望的SNR损失为0.8dB，要求 M=7dB，因为 ADC的有效输入噪声为 -61dBm，要求接收机的输出噪声为 -61+7=-54dBm。如果接收机的噪声系数是F1=3.5dB，带宽B=1MHz，那么接收机的等效输入噪声功率为kTBF1=-114+3.5=-110.5dBm，因此接收机的增益为G=-54-(-110.5)=56.5dB。将接收机的噪声系数F1，接收机的增益G，以及在前面算出的ADC的噪声系数F2的分贝值转换成实际数值，并根据噪声系数的计算公式:

计算出接收机和ADC级联后的实际噪声系数为4.29dB，即噪声系数恶化了4.29-3.5=0.79dB，因此信噪比损失和噪声系数损失是相同的。

8 模拟接收机增益的调整

ADC的有效输入噪声功率是一个非常重要的指标，它随测试点的不同而异。为了使整个接收机系统的SNR损失和ADC的动态范围损失能够满足给定的要求，必须通过微调接收机的增益来调整接收机输出噪声的大小。比如我们只能容许0.65dB的SNR损失，由图6可以查出此时对应的动态范围损失为7.9dB。那么调整接收机增益的方法如下:a.首先需要对ADC进行单独测试。将ADC的输入端接入匹配负载，用ADC对噪声进行采样。选择测试点，并对噪声电平进行测试，记其值为NΔ;b.然后将ADC级联在模拟接收机之后，重新对噪声进行采样，回到测试点对输出噪声功率进行测试，并微调接收机增益，使测试点的输出噪声功率的大小刚好比NΔ大7.9dB，那么此时的接收机增益必然能满足0.65dB SNR损失的要求。

9 大信号对ADC噪声的影响

除了热噪声和量化噪声以外，孔径误差是影响ADC性能的另一个重要因素［2］。孔径误差的示意图如图7所示。

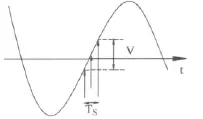
图7 孔径误差示意图

孔径误差的来源有两个［1，2］:一个是采样时钟的抖动(clock jitter)而引起的采样电压的变化;另一个是采样保持电路在每次取样时的时间延迟不同而引起的采样电压的变化。因而孔径误差的大小与输入模拟信号的变化速率有关。比如一个正弦输入信号x(t)=Asin(2πfot)的最大变化速率dx(t)/dt|t=0=2πfoA，因而可以看出，采样电压的抖动与输入信号的振幅和输入信号的频率有关，这意味着当大信号或高频率信号输入到ADC时，ADC的噪声基底将会抬高;另一个影响ADC性能的因素是ADC的非线性失真。非线性失真在大信号时尤其明显。非线性失真的后果是产生谐波分量从而导致噪声基底的进一步抬高。因而在大信号时，ADC的噪声电平会大于小信号时的噪声电平，这就是大信号压制小信号的问题。特别是在一个强干扰环境下，ADC对微弱信号的检测能力会急剧下降。影响ADC性能的另一个因素是大信号时导致ADC的饱和。ADC饱和后，输入信号的顶部被削平，从而产生较大的高次谐波分量。这些谐波分量最终会通过噪声基底的抬高而影响ADC的性能。因而为了使ADC避免大信号压制小信号的问题，来自ADC前端模拟信号的幅度被限制在FS之下1dB处。为了防止接收机输出信号的幅度超过ADC的满量程电压范围，在大信号时，接收机通过AGC电路来降低接收机的增益。例如通信接收机，对于最强干扰信号，需要通过AGC电路将接收机的增益降低6dB，这就会导致接收机的噪声系数降低约 1.6dB［5］。

10 脉冲压缩的增益

当输入端接收机中的信号是大时宽带宽积信号时，大时宽带宽积信号是雷达系统经常采用的信号形式，比如雷达系统中经常使用的脉冲压缩信号和通信系统中使用的PN码等，需要经过相关处理，或脉冲压缩过程来进行匹配滤波处理。脉冲压缩系统相比简单脉冲系统，有三个变化需要特别考虑:a.匹配滤波器的压缩增益;b.脉冲宽度的展宽;c.脉冲压缩损失。对于大时宽带宽积信号，匹配滤波器的处理增益为时宽带宽积TB，这里T是信号持续期的时间长度。B是信号的带宽。匹配滤波器的输出通常会产生较高的时间旁瓣，因而需要匹配滤波器失配来抑制时间旁瓣。但滤波器的失配会产生两个效果，一个是压缩后的脉冲宽度会被展宽，因而信号压缩后的等效带宽会下降。脉冲展宽的程度取决于加权函数。比如当采用Hamming窗函数加权时，压缩后的脉冲宽度由原来的τ=1/B，变为τW=1.32/B，即脉冲展宽系数为1.32。加权后的等效带宽BW由原来的B减小为BW=B/1.32。在计算过采样处理增益Go时，信号带宽B应该由脉冲展宽后的等效带宽BW来代替;另一个是加权带来的损失LM。因此必须从处理增益中扣除掉失配损失。总的匹配滤波器处理增益为:

采用脉冲压缩信号时，系统的动态范围会扩大。当模拟接收机的增益提高时，最小可检测信号功率降低，但同时对干扰信号的动态范围会被压缩。降低接收机增益，系统总的动态范围会扩大，最小可检测信号功率也随之提高，检测微弱信号的能力随之降低。因此系统必须在动态范围和最小可检测信号功率之间作出选择。无论如何，采用脉冲压缩信号可有效扩展系统的动态范围是不争的事实。

11 讨论

ADC的动态范围:当输入信号功率超过ADC满量程时，继续增加输入信号的功率并不会使ADC的输出功率立即被压缩。ADC在大信号时的动态范围可以线性扩展高达6dB。因此接收机的1dB压缩点可以设计在ADC满量程功率之上6dB处。虽然ADC饱和以后的输出功率并不会立即压缩，这意味着ADC饱和以后的输出SNR不会迅速恶化，特别是ADC饱和不会使Doppler的测量产生显著影响。但是ADC饱和以后会对其它指标产生影响，比如在脉冲压缩系统中，ADC饱和以后的时间旁瓣会迅速升高，从而产生大信号压制小信号的问题。如何设计接收机的1dB压缩点的位置则视应用场合不同而异。在简单脉冲系统中，如果我们比较关注的应用指标是信号噪声比，在外部干扰不是很强时，可将接收机的1dB压缩点设计在ADC满量程功率电平之上6dB处。在其它应用场合则必须将接收机的1dB压缩降低至ADC满量程功率电平以下。

高频大信号会导致ADC基底噪声的抬高，因而在数字中频接收机中，应尽量选择较低的中频。在遇到高频尖峰脉冲干扰时，ADC的检测性能急速下降。因而可在ADC满量程功率-6dB处设计一个自动增益控制电路AGC，使得在强干扰到来时，通过降低接收机增益来适应干扰。接收机增益的下降会导致噪声系数的下降，因而一个设计良好的系统必须规定在多强的干扰下，系统的检测性能下降多少。对简单脉冲而言，外部干扰信号和有用信号的动态范围是不同的。对于来自系统之外的干扰信号，其动态范围与简单脉冲系统相同。而对有用信号，因为可以检测到接收机灵敏度以下的微弱信号，因此动态范围被大大扩展了。因此接收机增益的选择必须在干扰信号的动态范围、有用信号的动态范围以及SNR损失之间作出权衡。

现在我们考虑这样一个问题，一个针对简单脉冲系统设计的接收机能否用于一个脉冲压缩系统，这个问题的提出源于下面的应用背景，假设希望通过发射一个大时宽带宽积信号来检测一个来自空间目标的回波。由于在脉冲发射期间接收机是关闭的，因此近距离的回波被遮挡了。解决距离遮挡问题的方法之一是将简单脉冲和大时宽带宽积信号组合起来，比如先发射一个窄的简单脉冲用于近距离检测，然后发射一个大时宽脉冲用于远距离检测。对于这个应用问题，是否需要设计两个接收通道对简单脉冲和大时宽带宽积信号分别进行处理，亦或可以使用同一个接收机通道来适应两种情况。

从第10节脉压增益的讨论可以看出，一个针对简单脉冲系统设计的接收机用于脉冲压缩系统时(假设模拟接收机的带宽在两种情况下都满足需求)，不论是检测灵敏度还是动态范围，脉冲压缩系统的性能均不会低于简单脉冲系统预测出的性能，反之则不然。如果特别针对脉冲压缩系统设计一个接收机通道，比如使用前面的“7dB准则”来设计接收机增益，那么这样的接收机用于简单脉冲系统时，由于SNR损失，其检测性能将急剧下降，可以说，不论是否应用于脉冲压缩体制，接收机的设计原则是一样的。一个原本为简单脉冲系统设计的接收机将会很好地工作在脉冲压缩体制的系统中，因此接收机系统的设计应优先考虑对简单脉冲系统的检测性能。

对于使用12-bit ADC的系统而言，ADC的动态范围是限制整机动态范围的主要因素(一般而言，接收机系统的动态范围大于12-bit ADC的动态范围)。除了可以采用脉冲压缩技术来扩展动态范围外，还可以考虑采用双通道接收机，即模拟接收机采用高、低两种增益组合来满足整个检测系统的动态范围，见图8。

图8 用双通道接收机构成的大动态接收系统

当高增益通道的ADC饱和时，使用低通道的ADC采样数据进行检测;当两个通道都没有饱和时，使用高增益通道的ADC采样数据进行检测。两个通道的增益一般相差20dB以上，可将整个系统的动态范围扩大至少20dB。

12 结论

本文从讨论ADC噪声电平开始，阐述了ADC噪声电平的测量，论证了采用过采样技术可提高ADC的信噪比，有利于减少接收机与ADC级联时引起的SNR损失和ADC动态范围损失。探讨了接收机增益的选择与调整，并通过一些举例计算，结果与理论分析完全吻合。分析表明，为了获得优化折衷的检测性能，接收机增益的选择应该使得接收机输出噪声功率高于ADC有效输入噪声功率7dB左右。

在数字中频接收机中，ADC的性能对整机的检测性能起着至关重要的作用。当ADC与接收机级联在一起时，ADC的噪声会降低接收机的检测灵敏度。检测灵敏度的损失、噪声系数的损失和信噪比的损失在量值上相等，它们只是从不同切入点对同一件事物的不同的表述。提高模拟接收机的增益可以降低SNR的损失，但是也会降低ADC的动态范围。因而模拟接收机输出噪声与ADC噪声电平的匹配实际上是在信噪比损失和动态范围之间进行权衡和折衷。权衡的依据是确定ADC的有效输入噪声功率的大小，它与所选择的测试点的位置有关，离开了测试点，谈论接收机噪声应该取多大是没有意义的。通常需要在匹配滤波器之后测量输出噪声，然后折算到ADC输入端。为了确定ADC有效输入噪声功率，可以对ADC进行大范围(超出动态范围)测量，然后通过画渐近线的方法确定测试点的输出噪声以及等效到ADC输入端的有效噪声。

对于脉冲压缩系统，ADC的有效输入噪声功率会比简单脉冲系统降低大约10lg(BT)dB。这意味着系统会检测到灵敏度之下约10lg(BT)dB的微弱信号。但这里对模拟接收机的增益无特殊要求。在简单脉冲系统中工作良好的接收机在脉冲压缩系统中也可以很好的工作，只不过要求它们的匹配带宽相同而已。

对于使用现代电子技术设计的接收机和ADC系统而言，35dB左右的接收机增益是一个合理地选择，过小或过大都是不可取的。接收机增益过大会导致动态范围的降低，因而不利于抗干扰，过小的增益会导致较大的SNR损失。

［1］James Tsui著，杨小牛，陆安南，金飚译.宽带数字接收机［M］.北京:电子工业出版社，2002.

［2］ 弋稳著.雷达接收机技术［M］.北京:电子工业出版社，2005.

［3］丁家会.数字化接收机极限性能指标的研究［J］.现代雷达，2005，9(27):72-74.

［4］ Burr-Brown.ADS2807:Dual 12-bit，50MHz Sampling Analog to Digital Converter［EB/OL］.http://www.ti.com/lit/gpn/ads2807.

［5］Maxium Application Note.Understanding ADC Noise for Small and Large Signal Inputs for Receiver Applications［EB/OL］.http://pdfserv.maxium-ic.com/en/an/AN1929.pdf.