航空铝合金应变空间弹塑性本构模型

张舒原，吴运新，龚海

(中南大学 机电工程学院，湖南 长沙，410083)

航空铝合金预拉伸厚板是航空航天与武器装备战略产业用高性能轻合金大型复杂结构件制造的基础材料，在大型军/民用飞机、战略航空武器装备中大量使用的整体结构件都会用到这类材料。目前制约我国高强铝合金厚板应用的主要问题是厚板淬火强化后将产生较大的残余应力，在后续加工中极易导致构建变形而报废。消除厚板淬火残余应力的最有效手段是厚板淬火后进行预拉伸。预拉伸工艺通过对厚板施加均匀塑性变形达到使厚板内部残余应力释放的目的。而建立厚板弹塑性增量本构模型是分析预拉伸消除残余应力机理的基础。目前用于铝合金材料的弹塑性本构模型都基于应力空间构建。当已知变量为应力时，可方便地求出板材内部应变。然而厚板可在线测试得到的物理量是应变和应变率，将其用于铝合金等强化材料的应力空间弹塑性模型时无法直接求解。由于航空铝合金预拉伸工艺的控制参数是板材轧制和横向的变形，其屈服函数不能简化为椭圆方程的形式，因而不能在应力空间的弹塑性模型中求得解析解。这一领域有关研究均是通过有限元数值仿真分析预拉伸应力，并结合实验数据来优化预拉伸工艺。采用应变空间表述的弹塑性本构模型可以直接由已知的变形条件求解出板内应力状态，为分析残余应力消减的宏观机理奠定基础。基于应变空间的弹塑性模型最初由Drucker[1]提出，但是这一领域最早的工作应该归功于 Naghdi等[2]的研究，他们将塑性应变和累积塑性应变作为塑性变形研究的状态变量。大部分研究者对这种变量更加熟悉。Yoder等[3]用塑性应力作为内变量建立了应变空间的屈服条件。Lu等[4]分析了应力空间模型和应变空间的等效性。他们的研究表明两种模型是等效的。应变空间弹塑性模型由于具有诸多优点，因此在混凝土、岩石、土壤等非金属材料的分析中得到广泛的应用[5-9]。然而到目前为止，应用于高强铝合金等线性等向强化金属材料的弹塑性本构模型研究未见报道。本文作者由岩土力学中使用的应变空间弹塑性应力应变一般关系出发，根据航空铝合金材料力学特征推导出适合等向强化金属材料的应变空间弹塑性增量本构模型，从而为超高强航空铝合金厚板预拉伸工艺机理分析奠定基础。

1 应变空间弹塑性本构模型

由于应变空间中屈服函数的实验研究较少，故应变空间中的屈服函数通常由应力空间屈服函数转化得到。应变空间里的屈服函数一般可表示为：

其中： εipj为塑形变形分量；H为加载历史的内变量，可以取为累积塑性应变或者塑性功，一般情况下使用前者更加方便。累积塑性应变[10]的定义是为偏应变张量增量的塑性部分。对于金属材料来说，无塑性体积变化，故所以有：

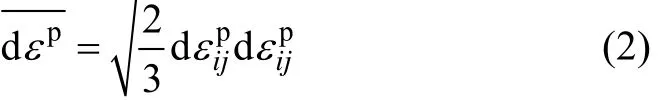
用应变空间的屈服函数可以给出如下的加载准则：

类似于应力空间中的流动法则，在应变空间也有与之对应的形式：

式中：ijklC 为材料的弹性刚度张量。且有

其中：E为材料的弹性模量；v为泊松比；ijδ为Kronecker符号。由式(4)和(5)可以得到：

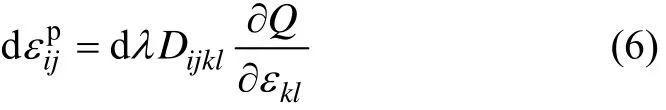
类似于应力空间中的定义，λd与应变增量之间有如下关系：

其中：A为比例系数。由于屈服函数F必须满足一致性条件，故由式(1)有

将式(6)和(7)带入式(8)则得到：

由d0λ≠，则可求出系数A的表达式：

将式(10)带入式(7)即可得到比例系数λd的表达式。由于材料的应变增量可以表达为弹性应变增量和塑性应变增量之和，故有

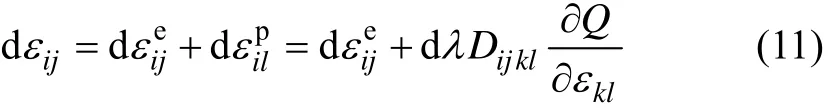
式(11)两边乘以 Cijkl，考虑到 Cijkldεe=dσ 及式(4)和(7)，经整理后可得应变空间弹塑性增量本构关系：

2 铝合金应变空间弹塑性本构模型

前面得到的本构关系式(12)是应变空间弹塑性增量本构关系一般表达式。要建立航空铝合金材料的弹塑性增量本构模型，还需要确定屈服条件、流动法则、塑性模量和强化函数。

2.1 屈服函数

航空铝合金材料属于强化材料，毋玲等[11-12]研究表明超高强航空铝合金材料具有明显的各向同性线性强化特征。因此本文选取各向同性线性强化作为材料的硬化模型。在应力空间中，以累积塑性应变为内变量的各向同性Mises强化材料的屈服函数可取为：

式中：J2为偏应力张量的第二不变量。由于J2和偏应变第二不变量 J2′之间的关系为，故式(13)可转化为应变空间中的屈服函数：

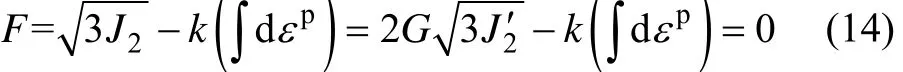
其中：G为剪变模量。式(14)可做进一步简化，但相应的强化函数等参量也要改变。为了方便与应力空间的塑性模型对照，保留式(13)中的形式作为应变空间中的屈服函数。由式(14)可以得到屈服函数对于应变分量的偏导数：

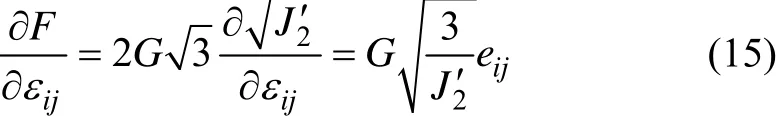
由于金属是稳定材料，故取屈服函数作为塑性势函数，即Q=F，以下均用F代替Q。

2.2 塑性模量和硬化函数

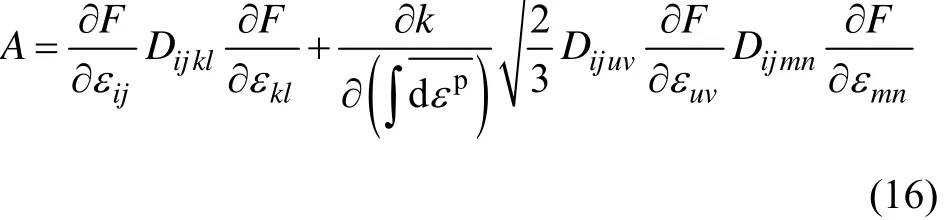
式(16)后半部分即为强化材料在应变空间里的硬化函数。由式(15)可得到以下关系：

将式(17)和式(18)带入式(16)可得系数 A的表达式：

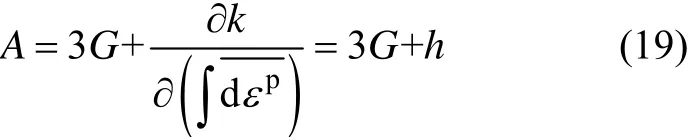
2.3 增量本构模型

由式(15)可推得：

将式(17)～(20)带入式(12)得到高强铝合金材料的弹塑性增量本构关系：

3 模型验证及分析

预拉伸工艺属于平面应力状态下的弹塑性变形[13-14]，厚板内部不同深度处可视为沿着轧制方向和横向呈一定固定比例的变形。文献[15]例题8.14中的变形条件与预拉伸工艺类似，故本文采用该题设定条件，将其计算结果作为已知应变条件输入本文模型反求应力，以验证本模型的正确性。现假定一铝合金金属薄板轧制方向(x向)和横向(y向)受均匀外力作用发生变形，产生的内应力变化路径如图1所示(简明起见量纲为1)。

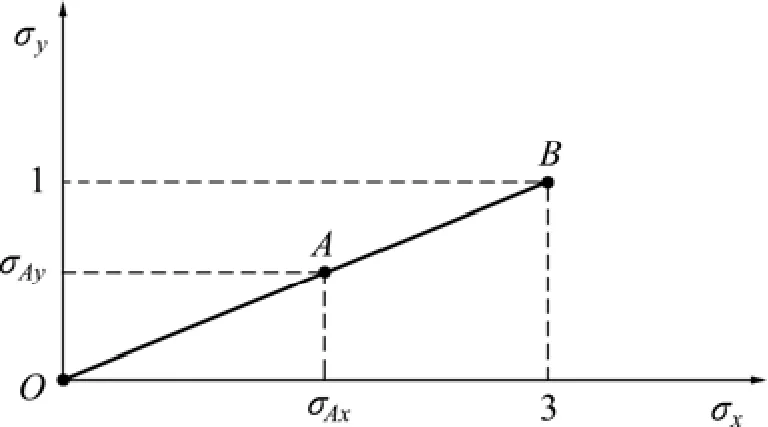
图1 薄板应力加载关系曲线Fig.1 Stress curve of loading on plate

薄板由初始点O开始比例加载至B点，2个正方向的应力成比例增大。设A点是初始屈服点，B点应力为已知材料强化特性是各向同性线性强化，应力空间的屈服函数为：原题将柏松比取为0.5，为避免弹性刚度张量在矩阵计算时分母取值为0，这里将泊松比的值取为0.499 9。由设定条件可知应力主方向和应变主方向重合，不存在剪应力和剪应变。

由平面应力状态下的Mises屈服条件，在A点有：

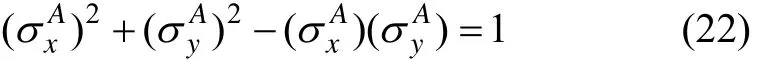
式中：上标A表示该变量是变形状态A点处的量，以下相同。由式(22)可求出屈服点A处的应力状态是：

根据应力空间的加载准则容易判断在 AB段薄板均处于加载状态。考虑应力空间关联正交流动法则和增量线性理论，用应力增量表达应变增量如下：

将A点应变和AB段应变增加量相加即可得到最终应变：

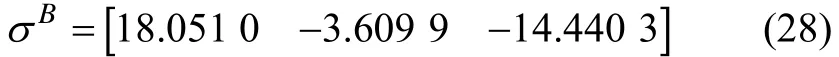
现用计算出的应变作为已知条件输入前述建立的应变空间弹塑性增量本构模型。由应力分量间的比例关系，容易由虎克定理计算出x和y方向的应变分量在弹性阶段(OA段)的比值是常数：

由式(24)～(27)可知：在弹塑性变形阶段(AB段)，x和y方向的应变之比也是常数：

上述应变关系如图2所示。

图2 薄板应变加载曲线Fig.2 Strain curve of loading on plate

根据弹性变形条件下的虎克定理， σij=Cijklεkl，容易求出初始屈服点A处的应力状态：

应变空间中的屈服条件由已知应力空间中的屈服条件转化得到：

对式(33)应变分量求偏导数的结果与式(15)相同。因此，本例中强化函数、比例系数等参量的表达式与式(16)～(20)中的形式相同。将材料常数及屈服条件代入式(21)，得到弹塑性变形阶段的增量本构关系如下：

AB段的应变分量可由下式表达

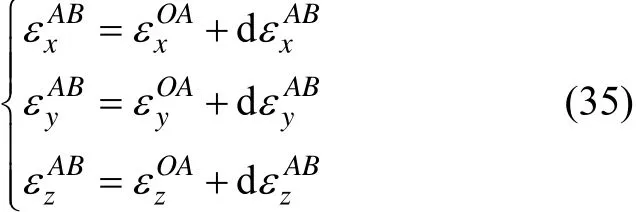
由式(31)，可以得到AB段应变增量间的关系：

将式(35)和(36)代入式(34)中的 eij和 J2′，则式(34)也可如式(24)一样简化为只含有表达式。将该式在塑性变形区间AB上对y方向应变路径积分即可得到塑性变形阶段的应力增量。对于x方向的应力增量，积分式的显式展开为：

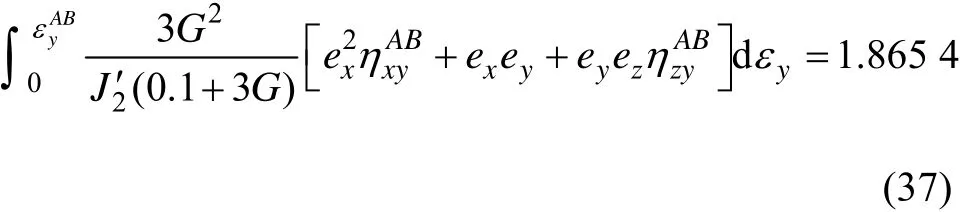
同理，可得到

将A点应力与AB段应力增加量相加即得到B点应力：

应变空间模型所得结果与题设基本一致。由上述计算可知本文建立的应变空间塑性增量本构模型与应力空间中的塑性增量本构模型等效。

4 讨论

式(39)的结果与精确值相比还有一定的差异，误差主要有2个方面的因素：一方面误差来自计算时的舍入误差；另一方面，计算中泊松比的取值接近0.5，造成弹塑性刚度矩阵 Cep接近奇异，从而导致模型对于输入误差的敏感度增强，放大了舍入误差带来的影响。若采用材料实际泊松比值(如对高强铝合金ν = 0.33)，则扰动会明显降低。

在实际应用中，板材厚度方向的应变难以实时准确的检测到，而应变误差的扰动对于应力计算的结果影响很大。因此，厚度方向的应变需要由轧制和横向方向的应变通过一定的关系模型求解，这样就可以进一步简化应变空间弹塑性模型的计算，并获得更为精确的结果。

通过前面的例题可以看出，利用应变空间塑性增量本构关系可以很容易地由已知应变求出应力，大大简化了工程实际应用时的计算。在高强铝合金淬火厚板预拉伸等工艺的应力测试和分析中，已知变量及实验可直接测试的物理量均为位移，因此应变空间中的弹塑性模型特别适合这些研究方面的应用。事实上，式(21)模型适用于所有各向同性线性强化金属材料的分析。通过对屈服条件、强化函数、塑性模量等条件的修改，该模型也可应用于Tresca强化材料。

5 结论

(1) 建立的应变空间塑性增量本构模型适合于高强铝合金等各向同性线性强化材料，该模型与应力空间的塑性增量本构模型等效。

(2) 基于应变空间的弹塑性本构模型可以由已知应变条件直接求得应力，在研究金属变形应力时使计算过程大为简化。尤其是对于强化材料来说，应变空间本构模型在使用上特别方便。

(3) 对于以累积塑性应变为内变量的线性强化材料，应变空间中的硬化函数等于应力空间的塑性模量，在计算中可以直接使用塑性模量的值作为应变空间模型计算时的硬化函数。

[1] Drucker D C. Some implications of work hardening and ideal plasticity[J]. Quarterly of Applied Mathematic, 1950, 7(4):411-418.

[2] Naghdi P M, Trapp J A. The significance of formulating plasticity theory with reference to loading surfaces in strain space[J]. International Journal of Engineering Science, 1975,13(9/10): 785-797.

[3] Yoder P J, Iwan W D. On the formulations of strain space plasticity pith multiple loading surfaces[J]. ASME Journal of Applied Mechanics, 1981, 48(4): 773-778.

[4] Lu P F, Vaziri R. The equivalence of stress- and strain-based plasticity theories[J]. Computer Methods in Applied Mechanics and Engineering, 1997, 147(1/2): 125-138.

[5] Casey J, Naghdi P M. On the characterization of strain-hardening in plasticity[J]. ASME Journal of Applied Mechanics, 1981, 48:285-296.

[6] Casey J, Naghdi P M. On the nonequivalence of the stress space and strain space formulations of plasticity theory[J]. ASME Journal of Applied Mechanics, 1983, 50(2): 350-354.

[7] Han D J, Chen W F. Strain-space plasticity formulation for hardening-softening materials with elastoplastic coupling[J].International Journal of Solids and Structures, 1986, 22(8):935-950.

[8] 夏旺民, 郭金晓, 郭增玉. 应变空间Q1黄土的弹塑性本构模型[J]. 岩石力学与工程学报, 2004, 23(24): 4147-4150.XIA Wang-min, GUO Jin-xiao, GUO Zeng-yu.Strain-space-based elasto-plastic constitutive model of Q1 loess[J]. Chinese Journal of Rock Mechanics and Engineering,2004, 23(24): 4147-4150.

[9] 梁立孚, 周平, 冯晓九. 应变空间中一般加载规律的弹塑性本构关系[J]. 哈尔滨工业大学学报, 2009(2): 187-189.LIANG Li-fu, ZHOU Ping, FENG Xiao-jiu. Elasto-plastic constitutive relation under general loading law in strain space[J].Journal of Harbin Institute of Technology, 2009(2): 187-189.

[10] 陈明祥. 弹塑性力学[M]. 北京: 科学出版社, 2007: 264-277.CHEN Ming-xiang. Elasticity and plasticity[M]. Beijing:Science Press, 2007: 264-277.

[11] 毋玲, 孙秦, 郭英男. 含点蚀损伤7075-T6铝合金拉伸性能数值模拟[J]. 机械强度, 2008, 30(5): 794-797.WU Ling, SUN Qin, GUO Ying-nan. Numerical simulation of the tensile behavior of al 7075-T6 alloy with corrosion pits[J].Journal of Mechanical Strength, 2008, 30(5): 794-797.

[12] 杨勇, 柯映林, 董辉跃. 7050航空铝合金“单因素”本构模型参数与温度相关性研究[J]. 航空材料学报, 2007(4): 19-24.YANG Yong, KE Ying-lin, DONG Hui-yue. Study on correlation between parameters of “single factor” constitutive model and temperature for 7050 aviation aluminum-alloy[J]. Journal of Aeronautical Materials, 2007(4): 19-24.

[13] Prime M B, Hill M R. Residual stress, stress relief, and inhomogeneity in aluminum plate[J]. Scripta Mater, 2002, 46:77-82.

[14] 王树宏, 马康民, 马俊. 预拉伸铝合金板7075T7351内部残余应力分布测试[J]. 空军工程大学学报, 2004, 5(3): 19-21.WANG Shu-hong, MA Kang-min, MA Jun. Method of measuring the residual stress distribution in pre-stretched aluminum alloy plate 7075T7351[J]. Journal of Air Force Engineering University: Natural Science Edition, 2004, 5(3):19-21.

[15] 黄文彬, 曾国平. 弹塑性力学难题解析[M]. 北京: 高等教育出版社. 1998: 70.HUANG Wen-bin, ZENG Guo-ping. Elasticity and plasticity problem analysis[M]. Beijing: Higher Education Press, 1998: 70.