聚类分析算法改进及其在地铁隧道病害分析中的应用研究*
2012-06-21丁小兵
丁小兵
(上海工程技术大学城市轨道交通学院,201620,上海∥助教)
隧道病害关系到轨道交通、公路的正常运营。据统计,隧道病害的种类有上百种之多,而目前隧道病害的处理方法虽然多种多样,但大都采用逐个病害排查的方法,浪费时间、人力资源等。本文在深入研究经典算法基础上提出了一种改进算法,通过基于最小支撑树的聚类算法的改进,采用改进的模糊聚类算法以及病害等级评价方法,对隧道的病害检测数据进行聚类分析,得出聚类结果;对隧道病害提出若干整改意见和建议,为隧道病害预防和整治提供有实际应用意义的参考。
1 k-均值算法
k-均值算法以类内平方误差和函数为目标函数,用户事先指定k个划分,通过梯度下降法迭代优化目标函数,使目标函数值最小[1]。该算法对于聚类个数k而言,本质上是一种枚举法。而k-均值算法又是硬划分的一种,每个划分至少包含一个对象,每个对象必须只属于一个划分[2]。
假设将n个样本X=x1,x2,...,xn划分为k个类,ni表示第i类中所包含的样本个数表示第i类的中心。则uij有如下定义和性质[3]:

第i类的类内平方误差为:
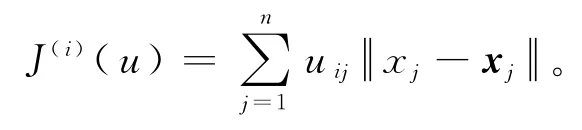
目标函数表示为:

通过迭代,使得J(u)取得最小值:J(u)*=min{J(u)},从而找到最优化。
针对k-均值算法,当聚类内部密集,且各聚类之间区别很明显时,该算法的效果较好[4]。
2 改进的聚类算法MK-means算法
在研究经典算法的基础上,对k-means算法进行改进,提出 MK-means(Mended K-Means)算法。在标准的k-均值算法中,初始点的选取是随机的。基于随机选取的初始点进行迭代运算,每次运行k-均值算法都会产生不同的聚类结果。而MK-means算法基于图论中最小支撑树的思想,通过求最小支撑树得到最小圈,产生k个初始聚类中心,得到更好的聚类结果。将该改进的算法用到隧道病害划分与预防中,具有很好的准确性和操作性,MK-means算法能够优化k-均值算法的性能。
2.1 MK-means算法
设连通图G=(V,E),每一边e=[vi,vj]有一个非负权w(e)=wij,wij≥0。
定义1:如果T=(V,E′)是G的一个支撑树,定义E′中所有边的权值之和为支撑树T的权,记为w(T),且
定义2:如果支撑树T*的权w(T*)是G的所有支撑树中最小的,则称T*是G的最小支撑树,也称最小树,即w(T*)=minw(T)[6]。
找到最小树以后,下一步要找到最小圈MC。
初始点选取过程如下:
首先,通过Prim算法找到最小树;
第二,通过上述算法找到最小圈;
第三,将最小圈包括的所有节点和边从最小树中除去,在剩余的节点中重新计算边长,产生新的最小树;
第四,迭代找出所有n+1-(n/k)个最小圈;
第五,计算n+1-(n/k)个最小圈的中心,作为初始聚类的中心。
通过以下的例子说明计算最小圈的过程。
以一个6个节点10条边的图为例,找出5个具有3个节点2条边的最小圈,这要求将6个点分成2个聚类。以下图1、图2和图3中线段旁的数字表示边长。图1表示工程原图,具有6个节点10条边;图2给出图1中的最小树,具有6个节点5条边;图3标明找到的5个圈:(1,2,3),(2,3,6),(2,3,4),(3,4,5),(3,4,6),虚线标志的圈为最小圈。

图1 工程原图
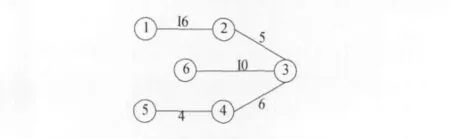
图2 最小树
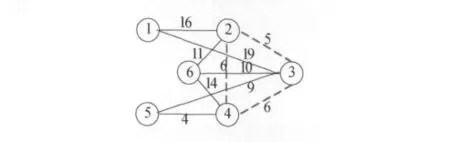
图3 最小圈
图1给出了工程原图,要找出最小圈,首先找出最小树,如图2所示。在最小树中,计算以任意两条边三个节点围成的圈的长度,图3中,L(1,2,3)=40,L(2,3,6)=26,L(2,3,4)=17,L(3,4,5)=19,L(3,4,6)=30。由此可见,由2,3,4三个节点组成的圈长度最小,即最小圈。最小圈的的中心就是k-均值中第一个初始聚类中心。然后,将节点2,3,4从图中删除,其余的节点为第二个聚类,由节点1,5,6组成的圈的中心为k-均值中第二个初始聚类中心。
MK-means算法包括两个步骤:初始化和聚类计算。初始化过程包括计算最小树,产生最小圈和计算圈中心三个部分[7]。假设数据集可以看成是一个由n个点,n(n-1)/2条边组成的连通图,每个数据被视为图中的一个节点,根据连通图的特点,每两个节点之间都有一条边,这条边的权重就是边的长度,每个聚类里面大约包含[n/k]个数据点。在初始阶段,要找出k个最小圈和k个初始聚类中心。
2.2 MK-means算法的流程
1)初始化。
输入:X=x1,x2,…,xn
输出:k个聚类中心
定义矩阵X=[x1,x2,…,xn]∥计算最小树
forj=1tok
定义一个空数组d=[]
令d1=x1
fori=1ton-1
ci=D(x′i,x′k=minD(xi,xk),xi∈d,xk∈X-d
di+1=x′k∥计算最小圈
fori=1 to(k-1)n/k+1
fi=c0+i+c1+i+…+cn/k-2+i+D(di,di+n/k)
fi=minfi∥计算最小圈中心Cj
Cj=means(di,…,di+n/k)
从数据集中删除最小圈中的数据点
j=j+1,X=X-d算法终止,直到j=k。
2)聚类计算,利用k-均值算法产生聚类。
3)输出聚类结果。
3 改进算法在隧道病害分析中的应用
将改进算法应用于部分隧道病害数据分析中,数据集为部分隧道的统计数据。因为试验数据的分类是已知的,所以本文采用相对标准分类的准确率来评判聚类结果。算法的评价指标如表1所示。

表1 改进算法评价指标
本文通过VC++编制程序实现记录识别,识别规则如下:
第一步,记录识别。如果记录i的“行别”=记录j的“行别”,且记录i的“线名”=记录j的“线名”,且记录i的“隧道号”=记录j的“隧道号”,且记录i的“隧道名”=记录j的“隧道名”,则记录i=记录j;否则,记录i≠记录j。
记录识别后,每条记录增加一个“隧道标识”属性,如果两条记录的上述4个属性都相同,则赋予相同的“隧道标识”。程序自上而下搜索,每一条记录都被比较一次,每一次比较都跳过作标记的记录,直到所有的记录都被标记。表2为贵昆线蜈松岭隧道记录识别示例。
第二步,记录重组。识别后的记录仍然不能直接用于聚类,还需要对劣化项目、劣化等级和数量等属性不同而其他属性相同的记录进行识别,添加隧道标号属性,标明记录所属的隧道,为聚类计算提供识别依据。

表2 贵昆线蜈松岭隧道记录识别示例
表3为通过VC++自编程序运行产生的隧道病害信息结果,为运用改进的聚类算法MK-means算法作准备。
通过基于最小支撑树聚类的改进算法运算,得出隧道病害主要聚类点和聚类距离,如图4所示。
由基于最小支撑树的隧道病害聚类生成图,得出隧道病害评价结果,如表4所示。
由表4可以发现改进算法MK-means的优点。
MK-means算法产生的分类结果准确率可达到0.88,且对于一个数据集,每次运行产生的结果都非常稳定,初始化之后,MK-means的聚类速度更快。改进的算法在结果准确性、稳定性、聚类速度等方面都优于k-均值聚类算法,它的结果稳定且接近最优结果。通过聚类可以得知:照明不良、衬砌开裂或错动、渗漏水、限界不足、隧道冻害为隧道的主要病害,运营管理部门应该有针对性地采取防治和预防措施。建议措施如下:
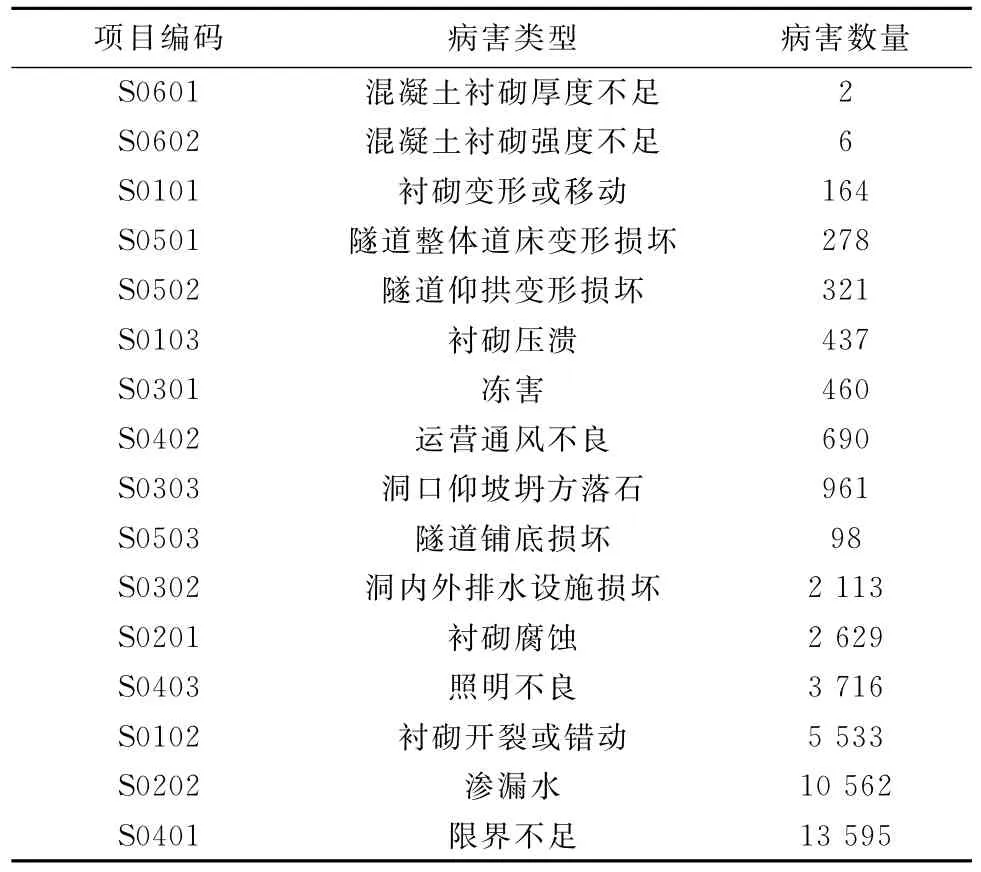
表3 通过VC++自编程序运行产生的隧道病害信息

表4 隧道病害评价结果
(1)衬砌渗漏水地段,采用“排为主,堵为辅,堵排结合”的措施。首先对衬砌背后进行全断面压注水泥,然后清理衬砌表面并涂刷止水涂层进行内贴式防水[8]。在集中出水处设置引水孔若干,通过排水管将水引至侧沟;无水沟侧则将水引至铸铁管,由铸铁管将水导人侧沟。
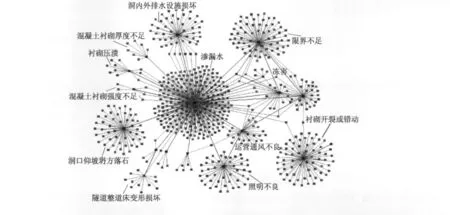
图4 基于最小支撑树的隧道病害聚类生成图
(2)对照明不良,应适当加强灯光照的强度,起到防晕的效果。
(3)对隧道冻害,严寒及寒冷地区隧道冻害的防治,可以采用综合治水、更换土壤、保温防冻、结构加强、防止融坍等,可根据实际情况综合运用。
[1]孙吉贵,刘杰.聚类算法研究[J].软件技术,2008,19(1):50.
[2]Ruspini E H.Numerical methods for fuzzy clustering[J].Information Science,1970,15(2):319.
[3]Tamra S,et al.Pattern classification based on fuzzy relations[J].IEEE Trans SMC,1971,1(1):217.
[4]Backer E,Jain A K.A clustering performance measure based on fuzzy set decomposition[J].IEEE Trans PAMI,1981,3(1):66.
[5]高新波.模糊聚类分析及其应用[M].西安:西安电子科技大学出版社,2004.
[6]李洁.基于自然计算的模糊聚类新算法研究[D].西安:西安电子科技大学,2004.
[7]Krishnapuram R,Killer J M.A possibilistic approach to clustering[J].IEEE Trans on Fuzzy System,1993,1(2):98.
[8]Selim S Z,Ismail M A.Soft clustering of multidimensional data:a semi-fuzzy approach[J].Pattern Recognition,1984,17(5):559.
