水下目标在水下爆炸作用下冲击响应的时频特征＊

李 万，张志华，周 峰，张 涛

（1.海军工程大学兵器工程系，湖北 武汉 430033；2.北京环球信息应用开发中心，北京 100094）

水下爆炸对水下目标的毁伤过程很复杂，整个过程包括炸药的水下爆炸、水下爆炸冲击波的形成和传播、水下爆炸冲击波和目标的流固耦合作用，以及水下目标结构在水下爆炸波载荷作用下的弹塑性动力响应等，深入研究水下爆炸对水下目标的毁伤效应对于水下目标的抗爆防护具有重要的意义。由于水下目标结构在水下爆炸冲击波载荷作用下的弹塑性动力响应常常是一个高度结构非线性的问题，因此对该问题主要采用数值模拟和实验相结合的方法进行研究。P.K.Fox［1］通过实验和LS－DYNA／USA程序模拟研究了远场水下爆炸冲击波对圆柱壳的毁伤效应；贾宪振等［2］利用通用有限元程序ABAQUS对深水环境中圆柱壳在水下爆炸作用下的毁伤效应进行了数值模拟。在已有的研究中，一般仅研究水下目标外壳结构的毁伤效果，有关水下目标内部装置毁伤效应的报道不多。然而，需要特别指出的是，水下目标内部装置由精细的电子功能元件组成，属于电子类产品，抗冲击能力较差，很容易因遭受冲击而损坏。所以说，要毁伤目标，不一定要使目标外壳破裂，如果能使目标受到足够大的冲击，造成目标内部装置振动而损坏，也可以毁伤目标。由于水下爆炸问题涉及流体和结构的相互耦合作用，建立的数学物理模型还不完善，因此通过有限元程序从力学角度揭示内部装置元件的毁伤机制不一定符合实际情况；而这可以通过从水下爆炸实验获得的水下目标内部装置冲击信号进行研究。

水下爆炸作用下的目标内部装置冲击信号具有突变快、持时短的特点，是典型的非平稳随机信号，信号分析要求具有较高的频率分辨率和时间分辨率。近年来，一些研究者用小波变换处理非平稳随机信号，并利用小波变换处理工程爆破振动信号取得了一定的应用成果［3］。本文中针对水下目标内部装置冲击信号的特点，利用小波变换的多分辨分解和分层的重构信号与原始信号间的基本关系，建立冲击信号时频特征分析的基本方法，以期取得冲击信号能量分布的某些特征。

1 基础理论

1.1 小波分析的基本理论

设ψ（t）∈L2（R）（L2（R）为能量有限的信号空间）是一个平方可积函数，若其傅立叶变换（w）满足允许条件［4－6］

则称ψ（t）为一个基本小波或小波函数（即小波基），称式（1）为小波容许条件。

将小波函数ψ（t）通过伸缩和平移后，就可以得到一个小波序列。对于连续的情况，小波序列为

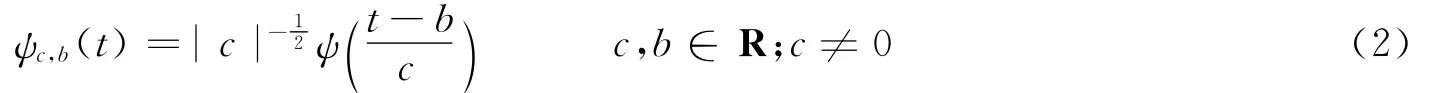
式中：c为伸缩因子，b为平移因子。

小波变换的实质是将一个任意信号s（t）以小波函数为基底进行展开，即将信号s（t）表示为小波函数的线性组合。对于任意能量有限的信号s（t）∈L2（R），其关于ψ（t）的连续小波变换定义如下

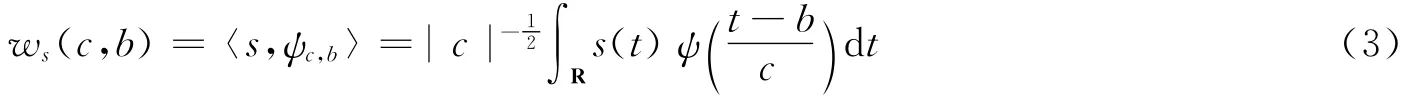
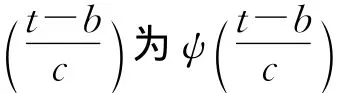
的共轭函数。

实际运用小波变换［7－9］时，伸缩因子c是按二进制进行离散的，即信号的频带是按指数等间隔划分的。若设采样频率为2f，则被分析信号频带为［0，f］，则经一层分解后，频带宽分别为［0，f／2］和［f／2，f］，每部分都经过一次减点抽样；再下一层的小波分解则是对频率成分［0，f／2］进一步分解，频带再分为［0，f／22］和［f／22，f／2］。如此类推，经N次分解后，即可得第N层的小波分解结果。

如果s0（t）表示实测信号，sr（t）表示小波分解后的完全重构信号，可以得到它们之间的相对误差

由于小波基函数存在多种可能的选择，小波分解的实际效果以及它与实测爆破振动的符合程度可以根据该相对误差的大小进行判定。

1.2 频带能量表征

小波多分辨率分析条件下，采用二进小波时，根据Mallat算法［4］，信号s（t）满足如下分层分解关系

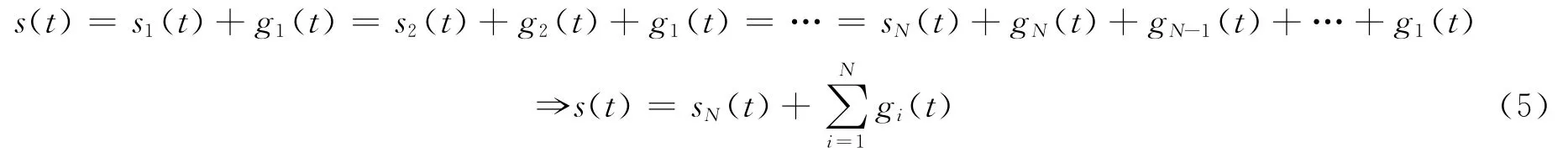
式中：si（t）表示为信号s（t）小波分解的低频部分，gi（t）表示为信号s（t）小波分解的高频部分，下标i表示所对应的分解层次。

为了使表达简洁，令信号g0（t）＝sN（t），则式（5）可以表达为

如果将信号s（t）进行N层的小波分解和重构，根据式（6）可得信号总能量

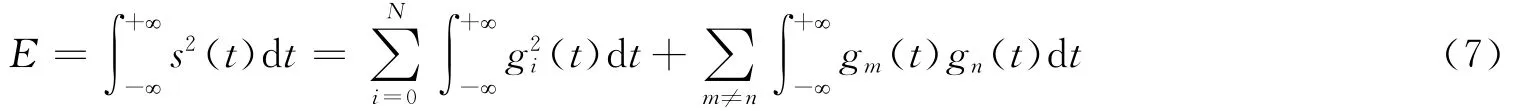
由小波函数的正交性可知，式（7）的第2部分为零，因此，式（7）又可简化为

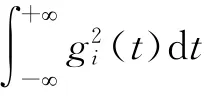
2 冲击响应实验

实验在大型水下爆炸实验水池中进行，考察小药量炸药的水下爆炸对某水下目标的毁伤效果。该水池水面直径为85m，池底直径为10m，水深15m，呈倒圆台型。将目标固定在水下8m处。考虑到工程实际，实验中以2kg球形TNT装药作为标准药包，水下目标与炸药放置在同一深度。由于是小药量炸药爆炸，水的自由表面和水底的影响可忽略，可近似认为炸药在无限、均匀、静止的水介质中爆炸。

根据爆炸理论和实际经验可认为影响目标损伤效果的主要因素有TNT质量、水深、爆炸距离r、方向角α等。实验时，在目标内部装置的元件底板上布设一个安装块，在相互垂直的轴向、径向和周向各安一个加速度传感器，在TNT质量、水深不变的条件下分别改变爆炸距离、方向角进行了多次实验。从测试得到的信号数据中选取具有代表性的4个工况的数据进行分析，下面以工况1轴向冲击加速度信号为例进行分析，其他信号的分析类似。

3 水下爆炸冲击加速度信号小波分解及各频带的能量分布

3.1 冲击加速度信号响应

实验时，考虑到水下爆炸冲击波持续时间短，设置水下爆炸加速度信号分析仪的采样时间为10μs。图1为工况1中水下目标内部装置的轴向冲击加速度曲线。

炸药在水下爆炸时，通常产生冲击波、气泡和压力波。高温高压气泡强烈挤压周围的水并向外扩散，于是便形成了初始冲击波。冲击波传播的同时还会伴随有气泡的脉动作用，并产生二次压力波，也会对水下目标造成破坏。冲击波引起的加速度幅值为2 004g，二次压力波引起的加速度幅值为324.3g，但是冲击波作用时间较短，频率高，二次压力波的作用时间较长，频率低。根据R.H.Cole［10］的水下爆炸理论，气泡脉动周期

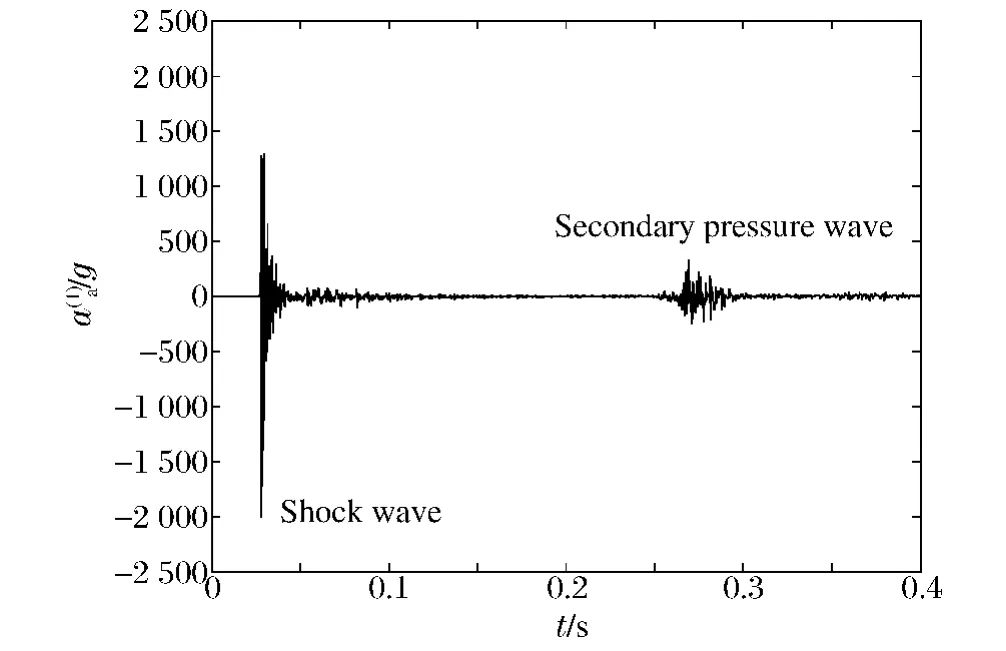
图1 工况1中水下目标内部装置的轴向冲击信号曲线Fig.1Axial shock signal of an interior device for the underwater target in case 1

式中：气泡脉动周期T，单位为s；m为炸药的质量，单位为kg；h为水深，单位为m。

由式（10）计算得到的气泡脉动周期为235ms，而测试得到的气泡脉动周期为241ms。由此可见，实验结果与用R.H.Cole的水下爆炸理论的计算结果接近，表明实验是可靠的。

3.2 冲击信号小波分解

（1）小波基的选择。小波分析中选择最优小波基很重要，因为用不同的小波基分析同一信号会产生不同的结果［5］。Daubechies小波系列具有较好的紧支撑性、光滑性和近似对称性［5，11］，已被成功地应用于分析包括爆破地震在内的非平稳信号问题［12］。而目前在非平稳振动信号处理中用得最多的是db4和db8小波。

（2）分解层数的选择。将信号进行小波分解时，由于本文中的采样频率较高，为100kHz，根据Shannon采样定理，则其奈奎斯特频率为50kHz。本文中用db4小波和db8小波分别对信号进行10层小波分解，可获得11个频带的小波分解系数。根据小波分解原理，11个频带宽度分别为：0～48.8、48.8～97.6、97.6～195.3、195.3～390.6、390.6～781.2、781.2～1 562.5、1 562.5～3 125.0、3 125.0～6 250.0、6 250.0～12 500.0、12 500.0～25 000.0和25 000.0～50 000.0Hz。

为验证小波包分解后的信号是否真实反映原始信号，对分解后的信号进行完全重构，根据式（4）计算完全重构信号与原信号的相对误差量级均在10－11以上，可完全满足工程计算和分析要求。计算中选择db4小波比选择db8小波的相对误差大，因此这里选用db8小波。所以，用db8小波对冲击信号进行分解的过程中，信号的能量损失可忽略不计。将11个频带分解系数重构后，获得上述11个频带的振动分量的时间历程曲线，如图2所示。

3.3 冲击信号各频带的能量分布

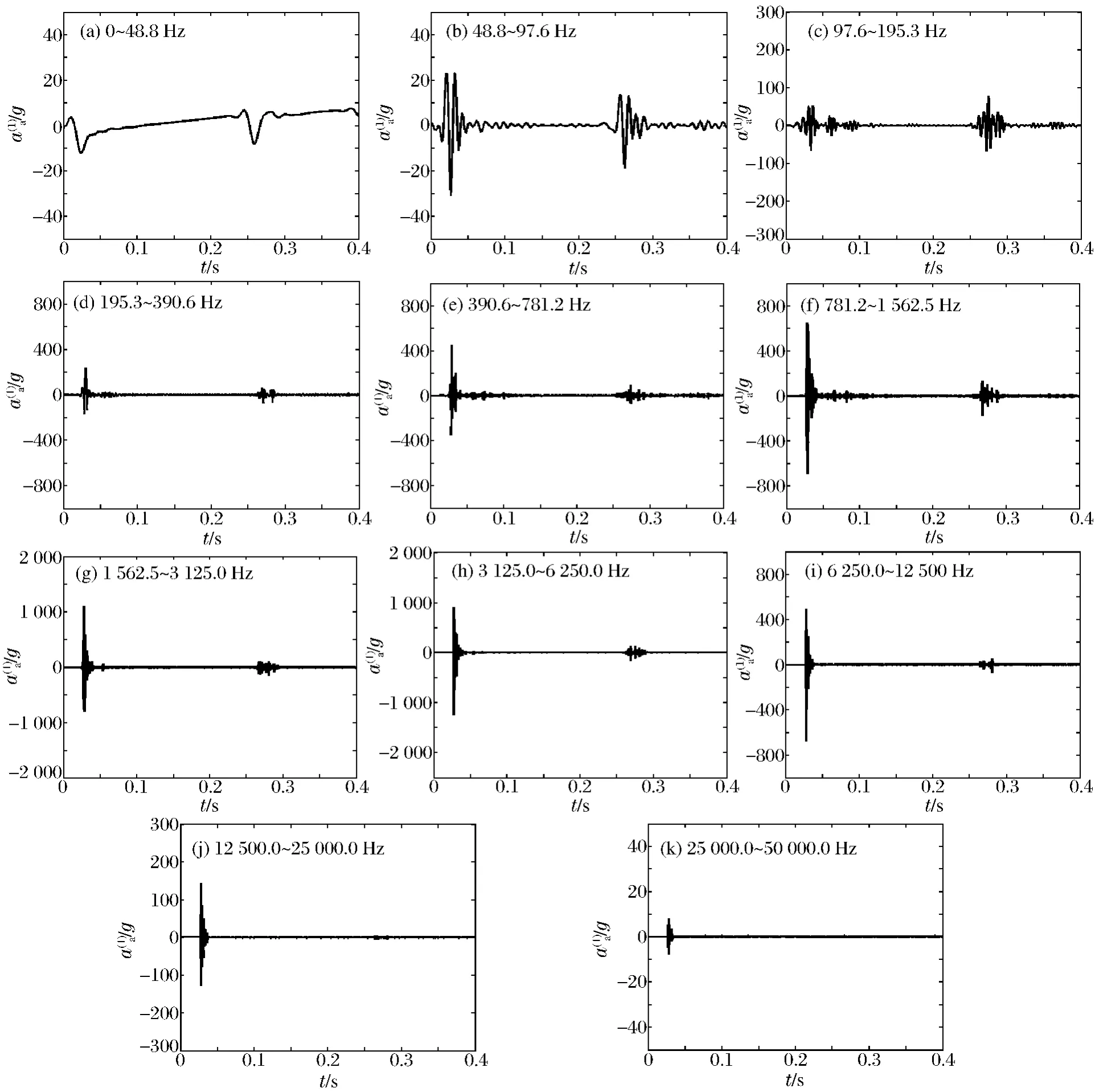
图2 工况1的轴向冲击信号小波分解后的分层重构信号Fig.2Reconstructed signals of axial shock signals in case 1undergoing wavelet decomposition at different levels

根据式（4）～（8）使用MATLAB语言编制计算程序，可获得工况1轴向冲击信号各频带f的能量分布／和加速度峰值，如表1所示。

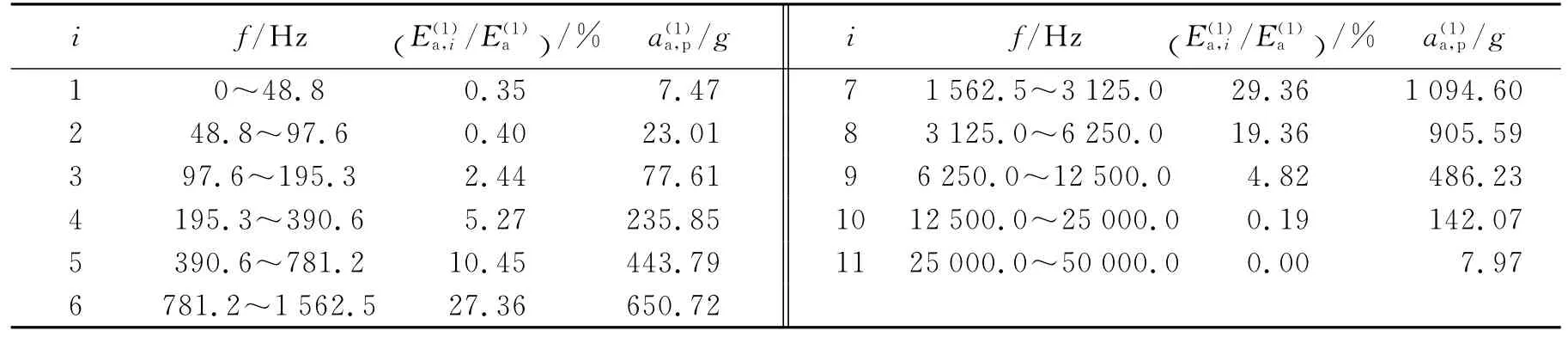
表1 工况1轴向冲击信号的频带参数Table 1Band parameters for axial shock signals in case 1

4 冲击信号的时频特征分析

（1）由表1可知，频带7（1 562.5～3 125.0Hz）冲击信号分量的小波频带能量最大。该冲击信号的最大峰值加速度所在频带也为频带7。也就是说，冲击信号的峰值加速度大小在一定程度上可由小波频带能量的大小来反映。因此，小波频带能量可以反映冲击信号强度对水下目标毁伤效果的影响。

（2）通过小波分析提取不同频带的冲击信号分量，获得各个频带冲击信号分量的小波频带能量，而小波频带能量大小直接反映了相应频带冲击信号分量的强度，从而可获取不同频带冲击信号分量对水下目标毁伤效果的影响。因此，小波频带能量可以反映冲击信号频率对水下目标毁伤效果的影响。

（3）由图2、表1可知，在低频带1～3，冲击信号分量衰减缓慢，振动持续时间较长，那么频带峰值加速度越大，小波频带能量就越大；在信号的高频带，尽管频带8冲击信号的频带峰值加速度比频带6的峰值加速度大，但所对应的相对能量较小。事实上，对比图2（f）和（h）不难看出，由于高频带8冲击信号分量的衰减较快，振动持续时间较短，所以小波频带能量较小。这个特点必须结合图2、表1才能发现，仅从表1的能量分布无法发现这一特点。同样，频带9冲击信号的频带峰值加速度比频带5的峰值加速度大，但所对应的相对能量较小。因此，小波频带能量可以反映冲击信号持续时间对水下目标毁伤效果的影响。

（4）在图2（i）～（j）的高频带，水下爆炸压力主要来自冲击波的压力，峰值大，持续时间短，衰减快，基本没有二次压力波的作用；从图2（h）才可以明显看出二次压力波的作用；由图2（g）可知频带7的振动加速度峰值最大；在图2（a）～（c）中，冲击波压力明显降低，衰减速度减慢；在图2（c）中，由二次压力波引起的振动加速度峰值已经超过由冲击波压力引起的振动加速度峰值。因此，用基于小波变换的时频分析方法可以获得冲击波和二次压力波在不同频带的分布和衰减的细节信息。

（5）为了进一步分析水下爆炸冲击信号中由冲击波和二次压力波引起的振动加速度能量分布，将冲击信号加速度信号分为2个阶段，以出现加速度峰值的时间中点为分割点，定义0～148ms为冲击波作用时间，148～400ms为二次压力波的作用时间。根据小波变换的分层重构信号可以得到在不同频率带上冲击波和二次压力波的能量分布情况，如图3所示。从图3能够直观地看出，冲击响应主要是受冲击波的作用，受二次压力波的作用可忽略不计，但在低频带1～3中由二次压力波引起的振动能量比冲击波引起的大。

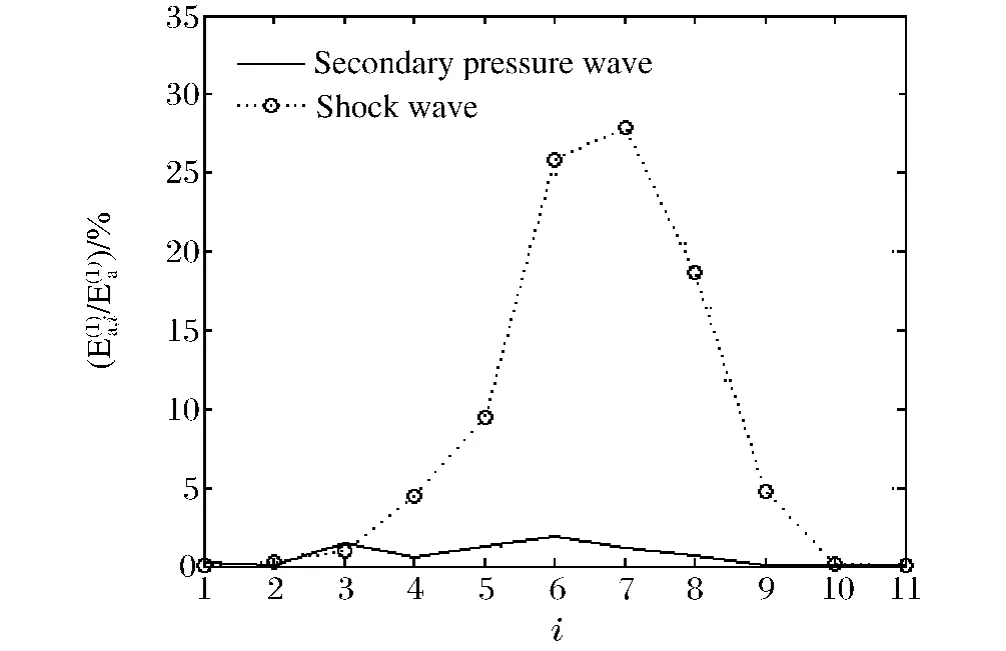
图3 在冲击波和二次压力波作用下工况1冲击信号在不同频带上的轴向能量分布Fig.3Axial energy distribution in different frequency bands for shock signals in case 1

（6）另外分析了其他3个工况冲击信号的能量E分布，如表2所示，表中量的上标2、3和4分别表示工况2、3和4，下标a、r和c分别表示轴向、径向和周向，下标i表示不同的频带。3个工况分别为：工况2，r＝3.5m，α＝45°；工况3，r＝2.5m，α＝135°；工况4，r＝2.0m，α＝90°。工况2冲击信号轴向、径向和周向总能量分别为9 687.4g2、2 847.2g2和2 452.1g2；工况3冲击信号轴向、径向和周向总能量分别为8 629.1g2、2 282.7g2和3 309.1g2；工况4冲击信号轴向、径向和周向总能量分别为8 950.3g2、1 278.3g2和3 027.2g2。3个工况下的总能量均表现为轴向总能量最大，远大于径向和周向总能量。由表2可以看出，冲击信号的能量分布很广，3个工况下在195.3～6 250.0Hz间3个方向上的能量分量分别占该信号相应方向上总能量的91.02%、96.75%、90.04%、97.05%、93.95%、97.45%、90.63%、87.08%和91.94%，而在0～97.6Hz间的相应能量所占比例很小。

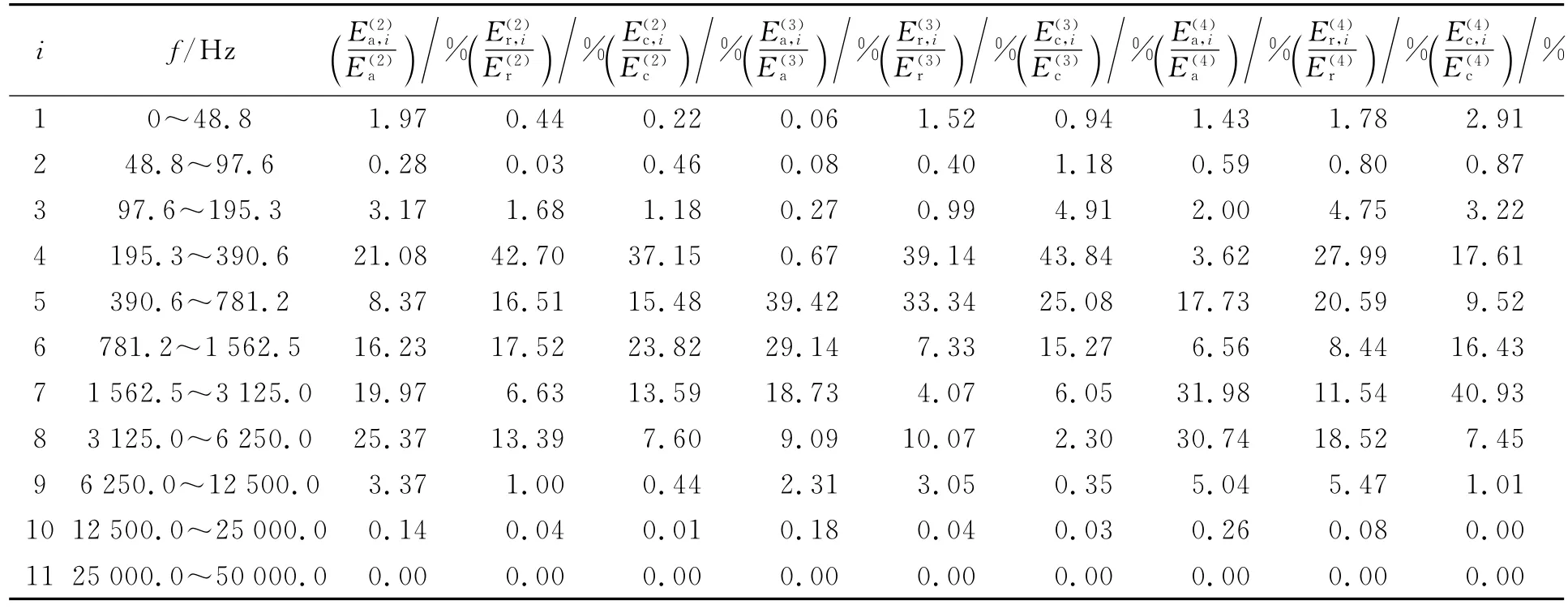
表2 不同冲击信号在各频带上的能量分布Table 2Energy distributions of different shock signals in different frequency bands

5 结 论

（1）建立了冲击信号时频特征分析的基本方法，小波时频分析的频带能量可以同时反映冲击振动的强度、频率和持续时间对水下目标损伤效果的影响，因此可以将频带能量作为水下爆炸毁伤水下目标的特征指标。

（2）从采用小波变换得到的不同频带的时间历程曲线，可以获得冲击波和二次压力波在不同频带上分布和衰减的细节信息。

（3）通过冲击信号时频特征分析得到冲击波和二次压力波引起的冲击信号能量分布，可以直观地看出，水下目标内部装置冲击响应主要是受冲击波的作用，受二次压力波的作用可忽略不计，但在低频带1～3中由二次压力波引起的振动能量比由冲击波压力引起的大。

（4）3个方向总能量的一般近似规律为轴向总能量最大，远大于径向和周向总能量；冲击信号的能量分布很广，但绝大部分能量集中于195.3～6 250.0Hz间，而在0～97.6Hz间的能量所占比例很小。

［1］Fox P K.Nonlinear dynamic response of cylindrical shells subjected to underwater side－on explosions［R］.ADA252856，1992.

［2］贾宪振，胡毅亭，董明荣，等.深水爆炸冲击波作用下圆柱壳动态响应影响因素的数值模拟研究［J］.高压物理学报，2008，22（2）：208－214.

JIA Xian－zhen，HU Yi－ting，DONG Ming－rong，et al.Numerical study on influencing factors of dynamic response of cylindrical shell subjected to deep water blast wave［J］.Chinese Journal of High Pressure Physics，2008，22（2）：208－214.

［3］李夕兵，张义平，刘志祥，等.爆破震动信号的小波分析与 HHT变换［J］.爆炸与冲击，2005，25（6）：528－535.

LI Xi－bing，ZHANG Yi－ping，LIU Zhi－xiang，et al.Wavelet analysis and Hilbert－Huang transform of blasting vibration signal［J］.Explosion and Shock Waves，2005，25（6）：528－535.

［4］Mallat S G.A theory for multiresolution signal decomposition：The wavelet representation［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1989，11（7）：674－693.

［5］Daubechies I.The wavelet transform，time－frequency localization and signal analysis［J］.IEEE Transactions on Information Theory，1990，36（5）：961－1005.

［6］胡昌华，张军波，夏军，等.基于 MATLAB的系统分析与统计：小波分析［M］.西安：西安电子科技大学出版社，1999：210－232.

［7］MA Guo－wei，HAO Hong，ZHOU Ying－xin.Assessment of structure damage to blasting induced ground motions［J］.Engineering Structures，2000，22（10）：1378－1389.

［8］Chui C K.An introduction to wavelets［M］.New York：Academic Press，1992：297－333.

［9］娄建武，龙源，方向.基于反应谱值分析的爆破震动破坏评估研究［J］.爆炸与冲击，2003，3（1）：41－46.

LOU Jian－wu，LONG Yuan，FANG Xiang.Study on blasting vibration damage based on response spectrum［J］.Explosion and Shock Waves，2003，23（1）：41－46.

［10］Cole R H.Underwater explosions［M］.New Jersy：Princeton University Press，1948.

［11］Daubechies I.Orthonormal bases of compactly supported wavelet［J］.Communication Pure and Applied Mathematics，1988，41（7）：909－996.

［12］林大超，施惠基，白春华，等.爆炸地震效应的时频分析［J］.爆炸与冲击，2003，23（1）：31－35.

LIN Da－chao，SHI Hui－ji，BAI Chun－hua，et al.Time－frequency analysis of explosion seismic effects［J］.Explosion and Shock Waves，2003，23（1）：31－35.