异型断面深基坑开挖与支护数值模拟分析
2012-06-15吕瑞虎李建华于少辉
吕瑞虎,李建华,于少辉
(中铁隧道集团有限公司技术中心,河南洛阳 471009)
0 引言
近年来,随着城市建设的迅猛发展,超深基坑的数量不断增多,其断面型式也逐渐从规则对称向复杂异型转变。以国内为例,采用超深基坑的工程有:北京国家大剧院基础埋深最深处为32.5 m,润扬长江大桥北锚碇基坑平均开挖深度达到48 m,上海轨道交通董家渡修复工程开挖深度达到41 m,外环隧道浦西暗埋段基坑、世博变电站等基坑开挖深度都达到了30 m以上。采用异型断面基坑的工程有北京西客站地铁车站、北京地铁六号线3标1号换乘厅、芜湖地下人防工程、深圳地铁车站一期工程、上海轨道交通某盾构措施井等。异型断面深基坑由于开挖深度大、断面异型及明显的空间效应,造成基坑内外应力场的非常态分布。如施工中未针对围护结构变形和受力特征采取有效保护措施,将引起基坑变形的加速,导致围护结构的破坏,对工程本身及周围环境都将造成不可估量的损失。文献[1]利用FLAC 3D有限差分法分析软件,对上海轨道交通某开挖深度为27 m的异型超深基坑进行建模计算,得出了该异型超深基坑的变形计算结果和变形控制要点。文献[2]结合某一地铁车站异型基坑,考虑基坑上下部分土体之间的相互作用对基坑稳定性的影响,分析了基坑在不同的水平台阶宽度情况下的稳定性。文献[3]对芜湖某住宅小区地下人防工程的异型基坑围护结构进行了工程设计研究。文献[4]研究不同的墙体刚度和支撑刚度对基坑地连墙弯矩、应力和水平位移、支撑轴力以及对基坑周围地面沉降幅度和范围的影响规律。文献[5]利用理论分析、数值模拟,对深基坑开挖过程中引起的土层位移、地表沉降分布规律以及支护结构的位移、应力改变等相关内容进行研究。文献[6]研究黄土深基坑在开挖进程中地表变形和支护结构水平位移变化规律。上述文献主要侧重于基坑开挖过程中围护结构和周围土体的变形、受力、稳定性研究,未涉及主体结构施作及拆撑过程中主体结构、围护结构、周围土体三者之间的协调变形及其受力特征。因此,以北京地铁6号线03标1号换乘厅为例,研究异型断面深基坑开挖及主体结构施作过程中主体结构、围护结构、周围土体三者之间的变形和受力规律,以期为今后类似工程提供借鉴。
1 工程介绍
1.1 工程概况
1.1.1 设计概况
朝阳门站位于东西向的朝阳门内大街与东二环路交叉路口以西,车站总长188.0 m,本站附属结构共设2个换乘厅、4个出入口、2个出入口兼换乘通道、3个换乘通道、1个无障碍出入口、1个疏散口及2个风道等。本工程为地铁6号线一期工程朝阳门车站附属工程1号换乘厅明挖基坑工程。
1号换乘厅位于东二环路西侧,中国海洋石油大厦东侧,南侧紧邻朝内大街交通主干线。结构位于中海油大厦东侧的绿地内,如图1所示。基坑长度为53.1 m,基坑宽为20.4(23.4)m,浅基坑深约16.7 m,深基坑深约31.2 m,顶板覆土3.36 m,采用明挖法施工,为目前北京地区最深异型基坑。支护结构采用围护桩+钢支撑+网喷支护体系。
1.1.2 工程地质概况
拟建场地平整后地形平缓,地面标高为43.3 m。场地内地层结构由上至下为人工堆积层(Qml)、第四纪全新世冲洪积层(Q4lal+pl)和第四纪晚更新世冲洪积层(Q3al+pl)。1号换乘厅明挖基坑穿过的地层情况由上到下依次为:杂填土①1层、粉土填土①层、粉土③层、粉细砂③3层、中粗砂④4层、圆砾卵石⑤层、粉土⑥2层及粉质黏土⑥层交错分布土层及圆砾卵石⑦层,局部为粉质黏土③1层、粉质黏土④层、中粗砂⑤1层及粉细砂⑦2层,基底位于圆砾卵石⑦层。根据工程地质勘察报告及工程经验,岩土层力学参数如表1所示。

图1 1号换乘厅深基坑工程平面布置图Fig.1 Plan of No.1 transfer hall project

表1 岩土层力学参数Table 1 Mechanical parameters of rock and soil strata
1.2 施工工序
见表2。
2 材料非线性计算分析理论
ANSYS中的Drucker-Prager(简称DP)准则是莫尔-库仑准则的近似,通常称为DP准则或广义密赛斯准则,是在密赛斯准则的基础上考虑平均主应力对土抗剪强度的影响而发展的一种准则。DP准则的屈服不随材料的逐渐屈服而改变,因此没有强化准则,其本构模型采用理想化弹塑性,可采用关联流动法则或非关联流动法则。该法则的屈服强度随着侧限压力的增加而增加,考虑了由于屈服而引起的体积膨胀,但不考虑温度变化的影响。该模型适用于颗粒状材料,如土、岩体、混凝土等。
DP 屈服准则可表示为[7]:

式中:{S}为偏应力,kPa;σm=1/2(σx+σy+σz)为平均应力,kPa;[M]为常系数矩阵。


式中:β为材料常数;σy为屈服强度;φ为材料的内摩擦角,(°);c为材料的黏聚力,kPa。

3 计算模型及假定
3.1 计算模型
基坑平面属于窄长形,开挖引起的变形主要以地表沉降和围护结构的侧向变形为主,沿基坑长度方向位移很小,因此,当进行数值模拟分析时,基坑变形符合平面应变基本条件。根据圣维南原理,左右边界取基坑跨度的4倍,下边界取基坑深度的2倍,最后确定计算范围为120 m×80 m。边界条件的约束为左右边界水平方向位移约束,下边界竖向位移约束[8],同时施加重力加速度以及地面荷载。
为简化计算,桩底以上各层土的物理力学性质指标按各层土的厚度加权平均计算[3]。

式中:γi为墙底以上各层土的天然重度,kN/m3;φi为墙底以上各层土的内摩擦角,(°);ci为墙底以上各层土的黏聚力,kPa,根据表1取值;hi为墙底以上各层土的厚度,m。
由于本工程不同于一般断面及平面均规则的深基坑工程,其周边不同部位围护结构的受力和变形差异较大,设计定义了A型、B型、C型3类钻孔灌注桩以适应本工程受力和变形复杂的特点(见图2),其桩径和间距分别为 0.8,1.0,1.0 m 和 1.4,1.4,1.5 m。本工程钻孔灌注桩的中心距均小于3倍的桩径,因此,可将其等效为板桩墙[9],从而可将间断布置的钻孔灌注桩简化为二维构件在模型中加入。等效后的板桩墙弹性模量E可按支护桩及桩间土的弹性模量的加权平均值进行计算,即
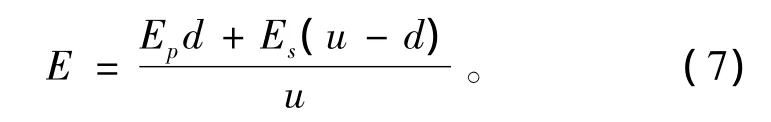
式中:Ep为桩的弹性模量,kPa;d为桩径,m;Es为桩间土的弹性模量,kPa;u为桩间距,m。
土体、等效后的板桩墙、主体结构均采用平面八节点单元,即plane 82单元,临时钢支撑采用beam 188单元,单元网格采用自由网格划分,且在桩、土、主体结构相互接触部分进行网格加密。通过包含“重叠单元”与“生死单元”的14个荷载步实现对基坑开挖、支护的模拟计算,整体结构及周围土体有限元模型如图3所示。
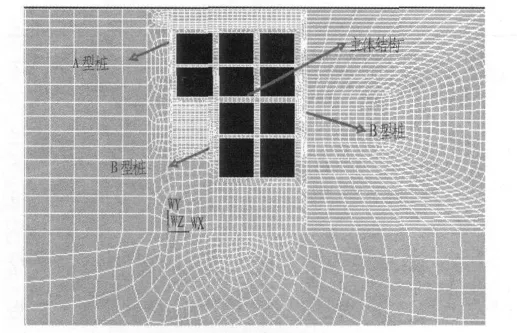
图3 整体结构及周围土体有限元模型Fig.3 Finite element model of integral structure and surrounding soil
3.2 计算假定
1)不考虑基坑降水及分步开挖对数值分析结果的影响。
2)假定钢支撑架设于开挖面标高处,不考虑0.5 m的施作空间。由于基坑开挖深度较大,此假定对计算结果的影响可忽略。
3)假定土体、围护结构、主体结构相互之间不存在接触滑动,即认为三者之间始终保持变形协调。
4)土体假定为符合DP准则的弹塑性体,围护结构、主体结构假定为线弹性体。
4 计算结果分析
4.1 变形分析
基坑主体结构施工完毕后,计算模型的水平和竖向位移分布情况见图4。由图4(a)可以看出:不同于一般规则基坑,计算范围内水平位移场不均匀分布。由于深浅基坑交接错台,使得深基坑底部位移变化较大,尤其是基坑断面左下角部水平位移明显大于其相邻部位。最大和最小位移发生于回填土范围内,说明基坑开挖和支护过程中发生较大的水平位移,对主体结构的施作精度产生不利影响。
由图4(b)可以看出:计算范围内的竖向位移场基本呈现以深基坑中轴为对称轴的均匀分布形态。基坑外两侧土体普遍沉降,基坑内下部土体则普遍隆起,且主体结构也存在一定的隆起现象。但由于异型断面基坑中平台的存在,平台处成为沉降和隆起的分界面。
4.1.1 地表沉降分析
取深基坑左侧5个测点和右侧3个测点进行分析,测点的方位与每个工序下的累计沉降值如图5所示。
由图5可知:1)开挖1部土体时,地表最大累计沉降值为0.37 mm;2)当开挖深度为24.481 m时,最大累计沉降值达10.58 mm;3)随着开挖深度的不断加大,地表最大累计沉降值也不断变大,开挖至基底时最大累计沉降值已达整个工程施工阶段最大累计沉降量16.93 mm,与实际监测值12.69 mm较为接近;4)随着基坑的封底和主体结构由下向上逐层施作,封闭的结构控制了扰动土层应力场的继续扩散,自重应力的不断增大又使得土层应力场向初始应力场转变,这2种作用相互影响的结果表现为地表隆起。基坑封底至主体结构施作完成,地表最大隆起量为8.66 mm。
4.1.2 基底隆起分析
取深基坑断面底部中心和两侧共3个测点进行分析,测点的方位和在每个工序下所对应的累计隆起值如图6所示。

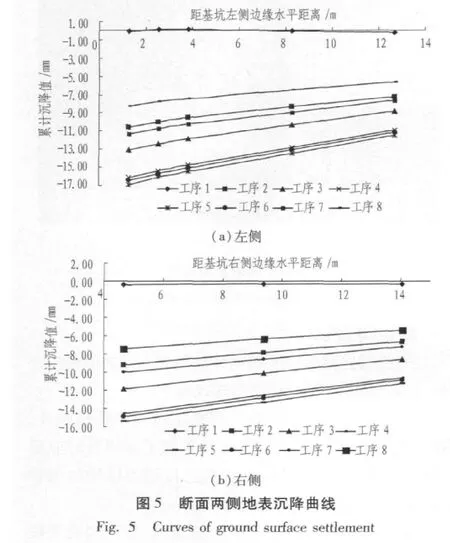
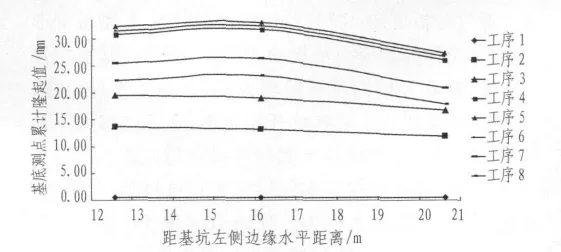
图6 基底隆起曲线Fig.6 Curves of uplifting of the floor
由图6分析可知:1)底部3个测点在每个工序下都存在隆起现象,且基本中部隆起较大;2)开挖1部土体时,基底最大隆起值仅为0.53 mm;3)当开挖深度为24.481 m时,最大隆起值已达13.76 mm;4)随着开挖深度的不断加大,基底隆起值也不断变大,开挖至深基坑基底时最大累计隆起量已达整个工程施工阶段最大隆起值33.05 mm;5)随着基底的封闭和主体结构自重应力的不断增大,这种“反压效应”使基底隆起量逐渐变小。基坑开始封底至主体结构施作完成期间,基底隆起量减小了9.91 mm。
4.1.3 围护结构水平位移分析
取A型桩等距5个节点,绘制A型桩在各工序下的水平位移曲线,正值表示向基坑内位移,负值表示向基坑外位移,见图7。通过分析可知:1)桩顶始终向基坑外位移,且一直增大至工程结束。2)随着开挖深度不断增大,负位移点逐渐增多,即桩体反弯点逐渐下移。至基坑开挖完毕,反弯点移至桩体中下部。此后至工程结束,反弯点虽略有上移,但其位置基本保持不变。3)桩端位移始终向基坑内位移,且在整个工程施工阶段,基本处于增大态势。尤其从开始施工到开挖至基底阶段,位移增速较大,其后一直保持较大位移。建议今后类似工程设计时应适当增加桩体长度,以保持围护结构的稳定性。

图7 A型桩侧向位移曲线图Fig.7 Curves of lateral displacement of Type A pile
由于土体开挖过程中,B型桩上部将被逐步切除,对其下部位移影响较小,故取平台以下B型桩等距5个点,绘制下部B型桩在各工序下的水平位移曲线,正值表示向基坑内位移,负值表示向基坑外位移,见图8。通过分析可知:1)当开挖深度较浅时,B型桩变形主要受土体原始应力场扰动的影响,桩顶向基坑内位移。2)随着开挖深度不断增大,桩顶向基坑外位移,桩体出现反弯点。至基坑开挖完毕,正负位移均不断增大,反弯点位于桩体上部接近错台的位置。此后至工程结束,桩体位移基本保持不变。3)桩端位移始终向基坑内位移,最大值为3.71 mm(工序5),建议今后类似工程施工时应适当加强桩体水平位移监测频率,保证施工及结构的安全。

图8 B型桩侧向位移曲线图Fig.8 Curves of lateral displacement of Type B pile
4.1.4 平台水平位移分析
由于异型深基坑中平台的存在,使得其变形特征比一般的深基坑更为复杂。选取平台上5个测点,绘制其水平位移图(如图9所示)。正值表示向基坑内位移,负值表示向基坑外位移,通过分析可知:1)随着土体开挖(工序1),平台发生基坑内的位移;2)当开挖至平台处(工序2),平台左半部基坑内位移增大,右半部由于坑底隆起效应影响产生基坑外位移;3)随着A型桩和B型桩通过平台连为一体(工序3),平台各测点位移均减少;4)随着平台下部土体的开挖,基底土压力不断增大,平台均表现为基坑外位移,并在工序5施作时达到最大值23.5 mm;5)随着后续工序的施作,楼板形成的框架体系约束作用明显,平台位移不断变小。鉴于施工中存在复杂平台变形,建议增强浅基坑基底下土体加固效果和范围,防止平台失稳坍塌,提高施工中维护结构可靠度。
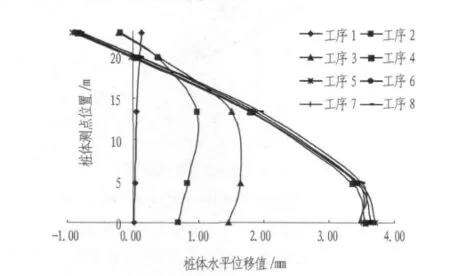
图9 平台水平位移曲线图Fig.9 Curves of horizontal displacement of the platform
4.2 受力分析
图10为工序4和工序8的整体有限元模型等效应力云图。通过分析可知,围护桩与钢支撑接触点、围护桩与主体结构接触处以及深浅基坑交界处的错台面均存在较大的等效应力,说明在这些部位存在明显的应力集中现象。建议以主体结构满足设计要求为基础,在围护结构施作、主体结构回筑过程中、应力集中部位可选用有效的连接或接触措施,如选用半刚性节点、设置柔性层等,确保结构与围护桩密贴并允许少量变形,以缓解应力集中现象,避免结构遭受破坏。

图10 等效应力云图Fig.10 Cloud of equivalent stress
5 结论与建议
通过对异型断面深基坑开挖与支护的数值模拟分析,并结合施工经验,结论与建议如下。
1)A型桩桩端在整个工程施工过程中位移较大,且一直处于增大态势,建议今后类似工程设计时应适当增加桩体长度及与B型桩的连接刚度以增加围护结构的稳定性。
2)该异型断面深基坑开挖深度大,易对周边环境产生较大影响;而4层楼板形成的框架体系约束作用明显,为控制围护变形提供了有利条件,可供其他异型基坑设计参考。
3)异型基坑的内支撑体系布置应充分考虑基坑异型带来的薄弱点,重点关注结构断面的变化点(特别是水平台阶处)。通过快速及时完成A,B型桩之间的连接、增大平台下部钢支撑的刚度和预应力等措施确保平台稳定。
基于建模简便采用了较多假定,计算结果与基坑实际变形特征可能存在一定程度的差异,且未进行土体与围护结构、围护结构与主体结构之间的接触分析及整体模型三维数值模拟分析,建议今后此类研究应通过适当简化最大限度模拟实际工况,并对上述问题进行分析以充分考虑基坑空间效应。
[1] 侯玉伟.上海轨道交通异形超深基坑施工过程数值模拟分析[J].城市轨道交通研究,2010,13(6):28-31.(HOU Yuwei.Analog analysis of the numerical value of difform deep-pit engineering in Shanghai Metro[J].Urban Mass Transit,2010,13(6):28 -31.(in Chinese))
[2] 董月英,雷震宇,包旭范.异型断面基坑的稳定性分析[J].隧道建设,2004,24(1):64 - 67.(DONG Yueying,LEI Zhengyu,BAO Xufan.The analysis of stability of pit with unique section[J].Tunnel Construction,2004,24(1):64 -67.(in Chinese))
[3] 刘文白,王梦瑜,车寿川.芜湖地下人防工程异型基坑围护工程设计[J].岩土工程学报,2006,28(Z1):1600-1604.(LIU Wenbai,WANG Mengyu,CHE Shouchuan.Design of unique pit exterior-protected construction engineering on underground civil air defense in Wuhu city[J].Chinese Journal of Geotechnical Engineering,2006,28(Z1):1600 -1604.(in Chinese))
[4] 熊孝波,桂国庆,郑明新,等.基于ANSYS的深基坑围护结构变形数值模拟分析[J].地下空间与工程学报,2009,5(S1):1298 - 1305.(XIONG Xiaobo,GUI Guoqing,ZHENG Mingxin,et al.Numerical simulation of bracing structure deformation for a deep pit foundation based on ANSYS software[J].Chinese Journal of Underground Space and Engineering,2009,5(S1):1298 - 1305.(in Chinese))
[5] 杨贵生,李雨润,李雨辰.超深基坑支护开挖对土体变形影响数值模拟研究[J].铁道工程学报,2008,117(6):32 -35.(YANG Guisheng,LI Yurun,LI Yuchen.Numerical simulation study on the influence of extremely deep pit bracing and excavation on soil deformation[J].Journal of Railway Engineering Society,2008,117(6):32 - 35.(in Chinese))
[6] 赵敏,曹卫平,何晖,等.黄土地区某深基坑变形数值模拟分析[J].西安工业大学学报,2009(6):579-583.(ZHAO Min,CAO Weiping,HE Hui,et al.Numerical analysis of deformation characteristics for a deep pit in loess area[J].Journal of Xi’an Technological University,2009(6):579-583.(in Chinese))
[7] 王新敏.ANSYS工程结构数值分析[M].北京:人民交通出版社,2007:493-494.
[8] 李围.隧道及地下工程ANSYS实例分析[M].北京:中国水利水电出版社,2008:332.
[9] 陈福全,杨敏.地面堆载作用下邻近桩基性状的数值分析[J].岩土工程学报,2005,27(11):51 - 55.(CHEN Fuquan,YANG Min.Numerical analysis of piles influenced by lateral soil movement due to surcharge loads[J].Chinese Journal of Geotechnical Engineering,2005,27(11):51 -55.(in Chinese))
