水底隧道衬砌水压力折减系数估算
2012-06-15王建宇
郑 波,王建宇,吴 剑
(中铁西南科学研究院有限公司,成都 610031)
0 引言
计算隧道衬砌水压力的方法较多,主要有折减系数法、数值解析法、理论解析法及渗流分析法等。其中,以折减系数法最为普遍,该方法最早应用于水工隧道,并且在《水工隧洞设计规范》中提出了明确的水压力折减系数表。由于以往对公路、铁路隧道衬砌所受的水压力没有给予足够的重视,且折减系数方法使用起来相对简单,因此,在公路、铁路隧道中遇到类似问题时,多数通过借用《水工隧道设计规范》的有关经验和规定来确定衬砌水压力折减系数。但《水工隧道设计规范》中的折减系数并没有考虑衬砌渗透性、隧道尺寸、水头等因素[1]的影响,所以其适用性在公路、铁路隧道中受到了很大的限制。
目前,国内外学者对衬砌水压力的研究较多,研究结果表明,40~60 m水头是“全堵型”结构的临界水头[2-3]。当地下水位超过衬砌结构所能承受的临界水头时,“全堵型”衬砌类型不适用,并且“以排为主”的设计原则已经不能适应当前水环境的保护[4],在隧道防排水设计中采用“以堵为主,限量排放”准则,既减少了作用在衬砌背后的水压力,又不致因大量无限制排水对地下及地表环境造成难以弥补的破坏。研究成果中尚缺少适用性强的水压力折减系数计算公式,特别是缺少适用于工程设计的简化计算公式。
因此,本文以具有稳定水头的水底隧道衬砌外水压力折减系数为研究目标,通过分析衬砌水压力的作用机制,解析推导水底隧道存在注浆圈与不存在注浆圈情况下,隧道涌水量的表达式,通过比较隧道衬砌前后涌水量差异,导出水压力折减系数的简化公式;并以某海底隧道为例,通过对比分析并证明所推导水压力折减系数简化公式的适用性与合理性,以期为水底隧道衬切水压力的估算提供一个可靠的快速计算方法,为衬砌结构设计时水压力折减系数选取提供参考。
1 水压力作用机制
根据对地下水处治方法的不同,修建于地下水位线以下的隧道通常可以分为“全堵型”和“排水型”。在“全堵型”隧道中,衬砌不透水,作用在衬砌上的水压力为静水压力,是一种表面力;而对于“排水型”隧道,围岩和衬砌都是透水的,地下水是流动的,作用在衬砌上的水压力为渗透力,是一种体积力[5-8]。国内外许多学者对于隧道围岩渗透力作了大量研究,并且提出了许多有意义的研究成果。如:王建宇[2]通过对衬砌范围内渗透力的积分得出作用在衬砌上的水压力合力在数值上等于该处孔隙水压力。因此,可以把隧道水压力计算模型简化为“荷载—结构”模型,方便工程设计人员使用。
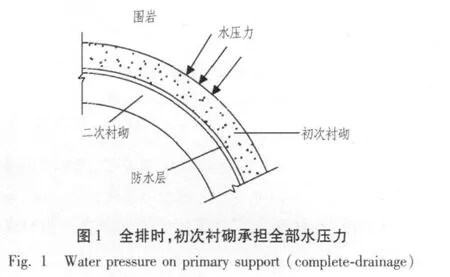
通常情况下,对于复合式衬砌类型的隧道,若不考虑围岩注浆,隧道排水系统能将渗透到衬砌(二次衬砌)背后的地下水全部排出,那么作用在二次衬砌上的外水压力可以忽略不计,外水压力主要作用在初次衬砌上,如图1所示。
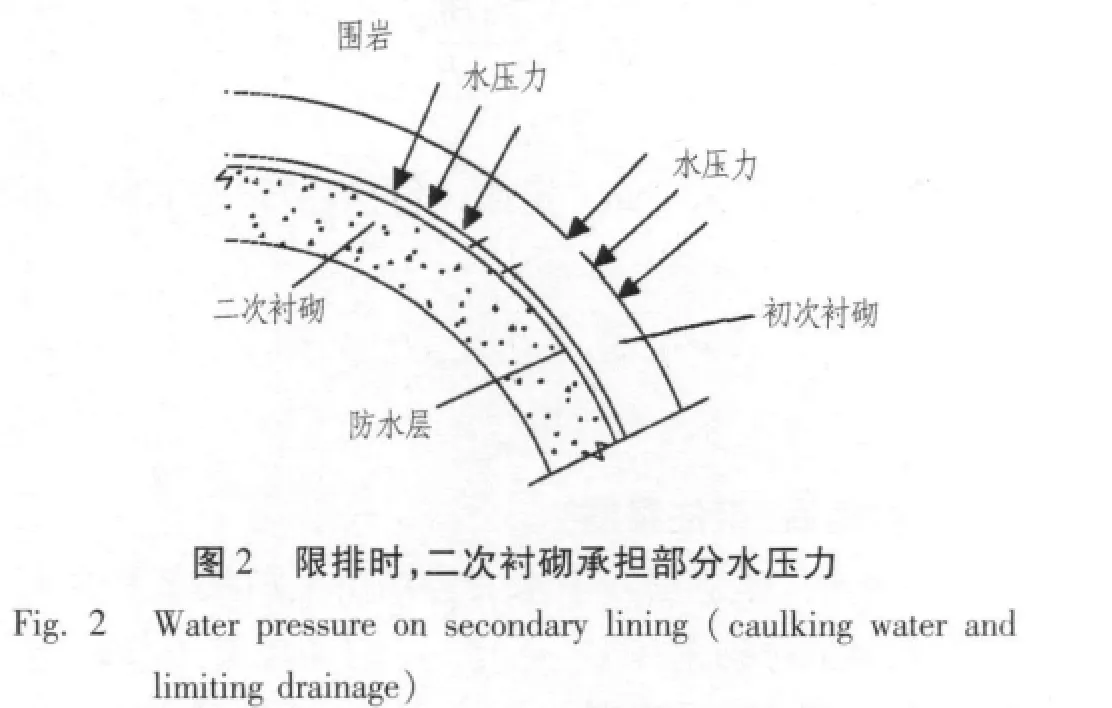
事实上,隧道通常处于复杂的地质环境中,排水系统会随着时间的推移产生堵塞而降低排水能力,导致作用在衬砌上的外水压力呈上升趋势。另外,在“堵水限排”的防排水原则下,为了控制地下水流量,当隧道设计排水量小于衬砌背后地下水量时,即排水系统只能排出部分渗透到衬砌背后的水量,二次衬砌会承担水压力。衬砌水压力由初次支护与二次衬砌共同承担,如图2所示。
注浆措施在海底隧道、高水头富水区隧道经常作为一种减少排水量,降低作用在衬砌上的水压力方法被广泛使用。注浆圈能有效减少涌水量,但注浆圈也将承受部分水压力,表现为渗透力,是一种体积力。另外,衬砌承担水压力,主要根据其本身的渗透性能、排导能力、注浆圈渗透性能及厚度等确定,当透过注浆圈后的渗流量较小,小于排水系统的排放能力,且排水系统畅通,那么二次衬砌将不承担水压力;若渗流量大于排水系统的排放能力或排水系统受堵时,二次衬砌将承担部分水压力。
2 水压力折减系数估算
依据无限含水层中井理论,把水底隧道围岩、衬砌渗流概括为承压水向垂直井的运动。并假定隧道断面为圆形,围岩为各向同性均匀连续介质,地下水渗流满足渗流连续性方程和Darcy定律,远水势恒定为H,不计初始渗流场,计算示意图如图3所示。
其中,kl为衬砌渗透系数;ks为围岩渗透系数;kg为注浆圈渗透系数;r为研究点的极距;r0为衬砌内径;r1为衬砌外径;rg为注浆圈外径。
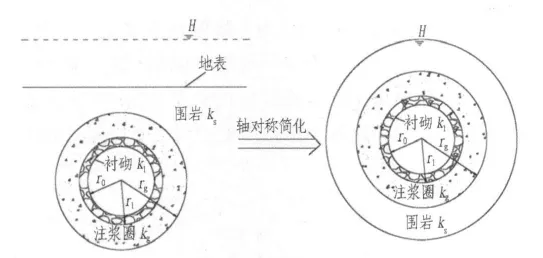
图3 圆形隧道计算示意图Fig.3 Calculation of reduction coefficient
2.1 开挖后,衬砌前(毛洞)
将指向隧道内的流量Q规定为正值,根据Darcy定律有 Q/2πr=ksdh1/dr,考虑边界条件 r=r1,h1=0,r=H,h1=H,对上式分离变量,然后积分可得衬砌前流量
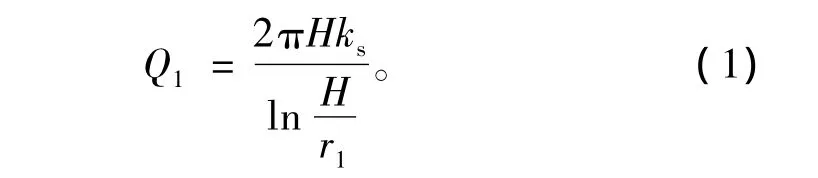
将式(1)代入Darcy定律,可得毛洞状态下围岩水力势
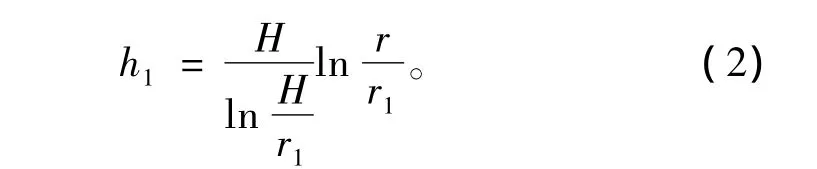
2.2 衬砌后(带注浆圈)
衬砌后,隧道围岩中水力势场由毛洞状态下的h1变为h2,在衬砌范围(r=r0~r1)内,有Q/2πr=kldh2l/dr,考虑边界条件 r=r0,h2l=0,可得

在注浆范围 (r=r1~rg)内,有 Q/2πr=kgdh2g/dr,考虑边界条件 r=rg,h2g=h2g',可得
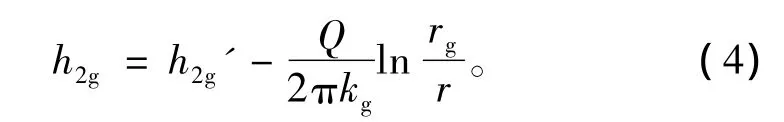
在围岩范围 (r=rg~H)内,有 Q/2πr=ksdh2s/dr,考虑边界条件r=H,h2s=H,可得

在r=rg边界上,即注浆圈与围岩交界处,根据水力势的连续性有h2g=h2s,把式(5)代入式(4)可得注浆圈范围内水力势

根据连续性方程,当r=r1,由式(3)和式(6)计算的结果也应该相等。故可以得出衬砌后流量
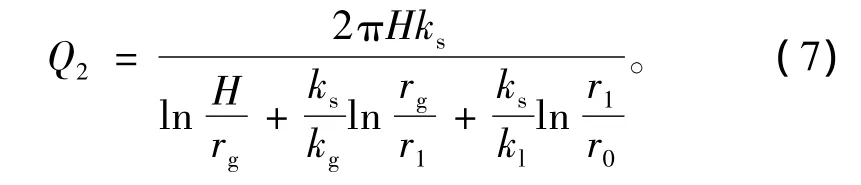
由式(3)和式(7)可得衬砌范围内水力势
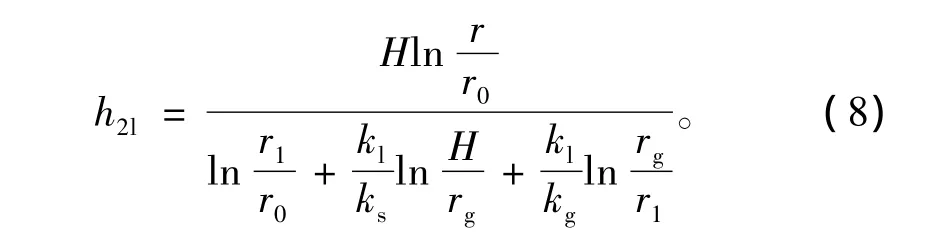
当r=r1,并考虑 H≫r1时,衬砌背后的孔隙水压力
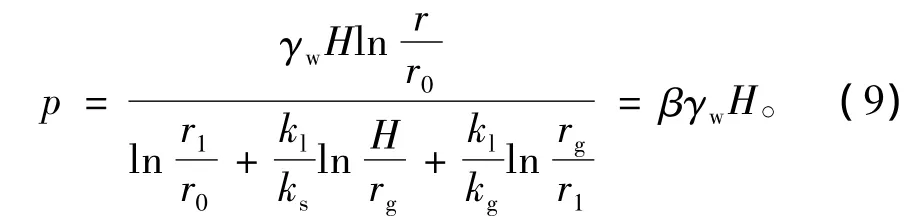
由式(7)可知,当隧道开挖后,带有注浆圈未衬砌的隧道涌水量可近似表示为
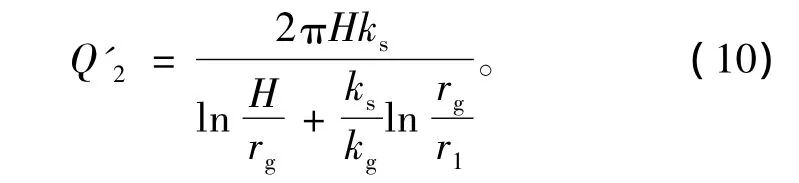
由式(7)、(9)和(10)可得
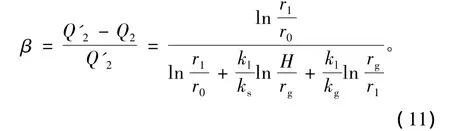
在围岩未注浆情况下,可令ks=kg,那么式(11)可以简化为
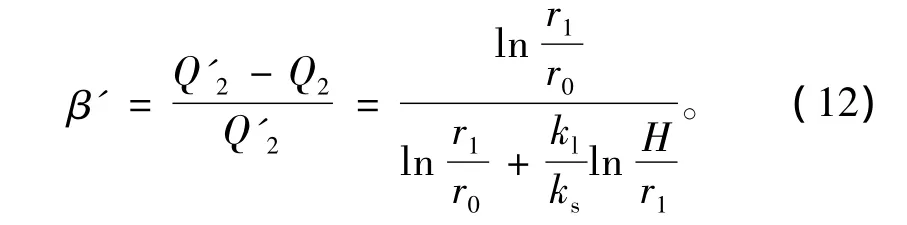
通过上述分析,对于水底隧道,通过现场测量或理论计算可以很容易得出Q'2,而Q2为隧道衬砌后的涌水量,通过集水井也是很容易得到的,那么在隧道修建及运营的过程中,作用在衬砌上的水压力折减系数可以由式(11)或式(12)求得。在隧道设计阶段,根据当地生态环境的要求及对地下水流量的控制标准可以估算作用在衬砌上的水压力,并可对隧道衬砌的水荷载进行动态设计。
3 数值试验及验证
3.1 数值试验概况
数值试验时,对计算模型做如下假设:1)围岩为均质、连续、各向同性介质;2)渗流属于恒定流且满足Darcy定律;3)隧道计算断面为圆形,水头恒定,不因隧道开挖排水而减变。
以某海底隧道的服务隧道为计算模型,如图4所示,该隧道为锚喷支护结构,衬砌内径r0=3.0 m,衬砌外径r1=3.2 m,隧道覆盖层厚度H=35 m,水深h=42 m。计算模型自隧道中心水平向外各取5D(D为隧道直径),垂直向下取5D,向上取值为实际覆盖层厚度,沿隧道轴向取单位长度,海水深度为42 m。
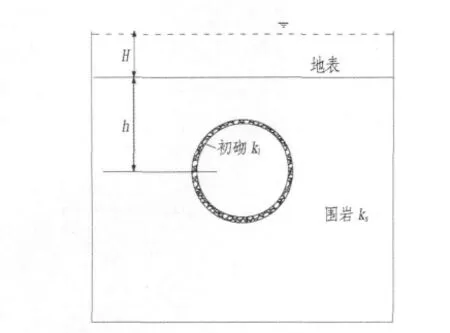
图4 数值计算模型Fig.4 Numerical calculation model
对未注浆围岩,围岩渗透系数考虑1×10-6cm/s和1 ×10-5cm/s 2 种工况,kl/ks考虑 0.5,0.1,0.05,0.01,0.005和0.001共6种工况。
对注浆围岩,围岩渗透系数为1×10-5cm/s,注浆圈渗透系数考虑1×10-6cm/s和1×10-7cm/s 2种工况,注浆圈厚度为3.0 m,kl/kg考虑 10,1,0.1,0.01共4种工况。
渗流计算采用单渗流模式,模型两侧为不透水边界;由于海水深度为42 m,模型上表面设孔隙水压力为4.2×105kPa,模型下表面也为不透水边界,隧道开挖后,设衬砌外侧孔隙水压力为0。
3.2 计算结果及比较分析
图5为渗流量与kl/ks比值关系曲线。从图5中可以看出,若隧道开挖后不衬砌,当围岩渗透系数分别为1×10-5cm/s与1×10-6cm/s,单位长度隧道内涌水量分别为1.44 m3/(m·d)和0.14 m3/(m·d)。衬砌后,隧道涌水量随着衬砌渗透系数减小而减少,而当kl/ks=0.001时,涌水量几乎为0。
图6为水压力折减系数与kl/ks比值关系曲线。从图6可知,由简化公式计算得出的折减系数与数值分析计算得出的折减系数类似,当kl/ks=0.001时,水压力折减系数近似为1,作用在衬砌上的水压力相当于静水压力;而当kl/ks接近1时,水压力折减系数近似为0,作用在衬砌上的孔隙水压力相对较小,在设计中通常可以忽略。从图6中可以看出,作用在衬砌上的孔隙水压力随着kl/ks的减小而减少,对隧道衬砌水压力的设计完全可以按本文所提出的利用衬砌前后涌水量的反分析公式计算。
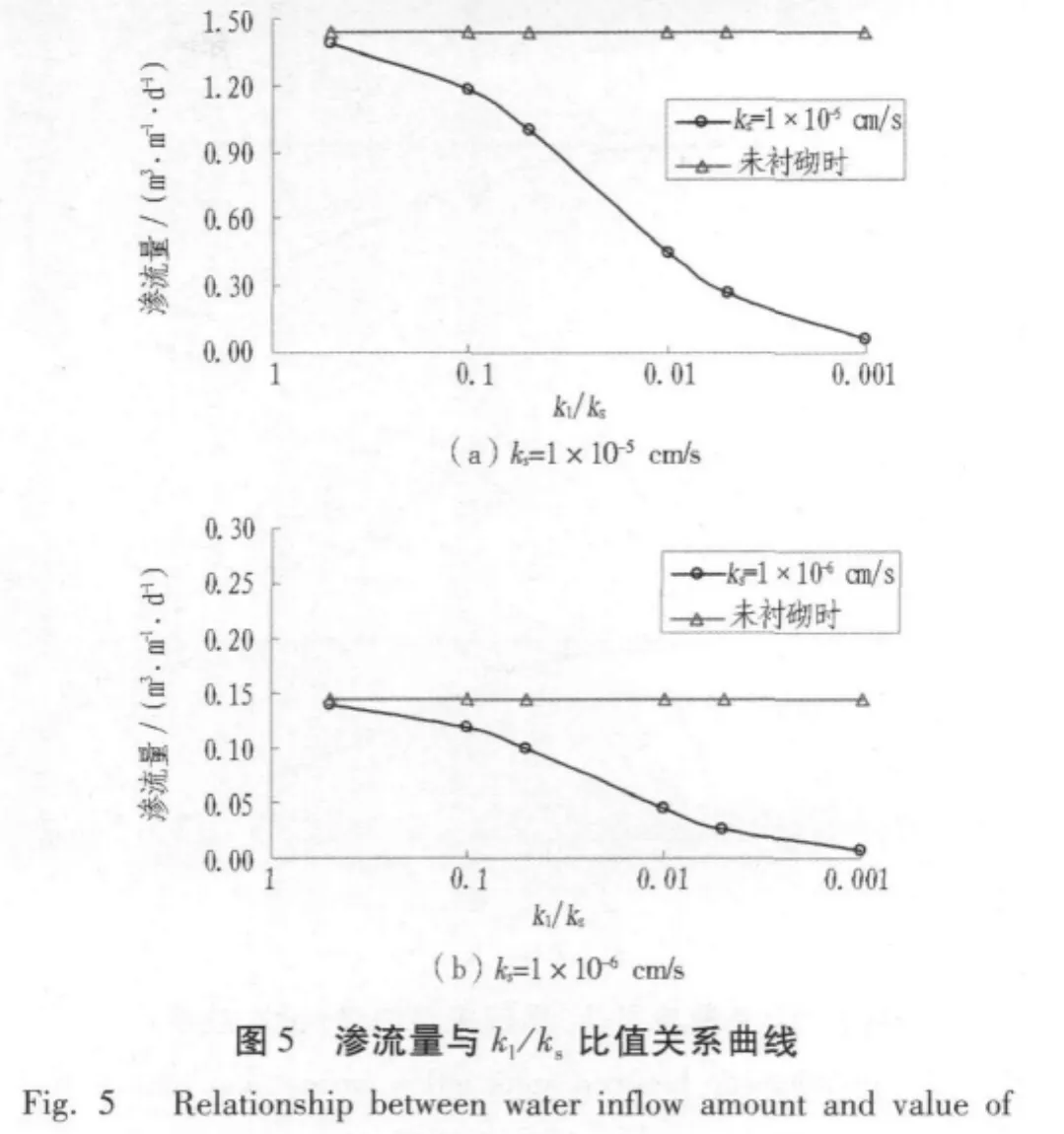

由图5和图6可以看出:对于不同的kl/ks值,水压力折减系数与渗流量存在一个公共点,也就是说在隧道防排水过程中,一味地减小渗流量,会导致作用在衬砌上的水压力增大,它们之间存在一个交点,这个交点范围为kl/ks=0.02~0.03,对应的水压力折减系数约为0.5;同时,一味地任渗水自由排出,则不满足当前环境保护的要求。所以,公共点是一个很好的经济指标,可以在隧道设计中加以应用。
图7为围岩注浆(围岩渗透系数为1×10-5cm/s、注浆圈厚度为3 m)时,渗流量与kl/kg比值关系曲线,由图7可知,注浆圈渗透系数为1×10-6cm/s时,不衬砌时渗水量从不注浆的1.44 m3/(m·d)减小为注浆后的0.47 m3/(m·d);当注浆圈渗透系数减小到1×10-7cm/s后,渗水量减少至0.06 m3/(m·d)。另外,从图7中还可以看出,kl/kg比值越小,涌水量越小。由此说明,围岩注浆能有效减少渗流量。
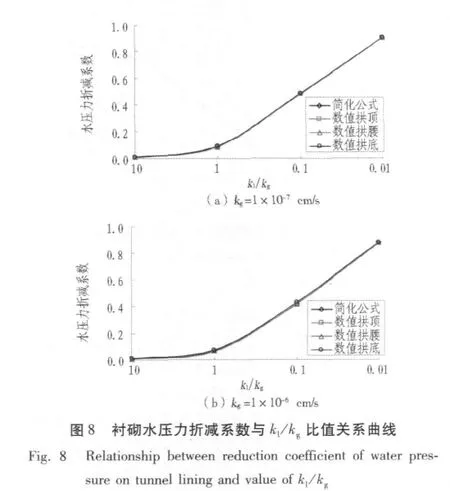
从图8中可以看出,当kl/kg大于1时,水压力折减系数很小,但当kl/kg减小时,衬砌水压力折减系数增大,当kl/kg=0.01时,衬砌上的水压力折减系数接近于1。由简化公式计算的衬砌上水压力折减系数与数值计算结果基本相同,又一次验证了简化理论公式的可靠性。但从图9可以看出,作用在注浆圈上水压力对kl/kg值不敏感,当kg=1×10-7cm/s时,注浆圈壁上水压力折减系数基本不随kl/kg值改变而改变,其值约为1;而kg=1×10-6cm,kl/kg=10时,注浆圈壁上水压力折减系数约为0.8,这主要是由于注浆圈较厚,在注浆圈范围内造成了较大的水头损失,表明对于“全排”隧道,注浆圈极大地减少了涌水量,但仍然会有较大的水压力作用在注浆圈上,这对注浆圈的耐久性提出了较高的要求,因为作用在注浆圈上的水压力基本不随时间变化,当注浆圈的强度降低时,不仅会增加隧道的涌水量,也会减小其强度,会给隧道带来安全隐患,这将是另一个值得深入研究的问题。


图9 注浆圈壁水压力折减系数与kl/kg比值关系曲线Fig.9 Relationship between reduction coefficient of water pressure on grouting circle and value of kl/kg
4 结论与讨论
本文从水底隧道衬砌水压力的作用机制出发,对水底隧道进行了轴对称简化,推导了存在注浆圈与不存在注浆圈情况下,隧道衬砌上水压力折减系数的简化理论公式,并通过数值计算验证了简化理论公式,其结果表明理论公式对衬砌水压力折减系数的反分析方法可靠、有效,可以在以后隧道设计中推广应用。
水下隧道衬砌水压力的确定问题,是目前隧道工程界尚未解决的一个难题。事实上,衬砌水压力是一个体积力,仅在一定条件下,才能等效成面力,进而利用“荷载—结构”模型进行工程计算与设计。本文是在一系列理想条件下进行推导的,没有考虑围岩介质的不均匀性,也没有考虑作用水头的变化等工程实际情况,因而计算结果可能和工程实际仍存在一定差距。所以,对于隧道衬砌水压力的确定,很有必要综合上述未考虑因素进行更深入地研究和分析。
[1] 王建宇.对隧道衬砌水压力荷载的讨论[J].现代隧道技术,2006(S):67 -73.(WANG Jianyu.Discussion on water pressure upon tunnel lining[J].Modern Tunnel Technology,2006(S):67 -73.(in Chinese))
[2] 王建宇.隧道围岩渗流和衬砌水压力荷载[J].铁道建筑技术,2008(2):1 -6.(WANG Jianyu.Problems on external water pressure on tunnel lining[J].Railway Construction Technology,2008(2):1 -6.(in Chinese))
[3] T S Nam,E J J,G C Choi,et al.Hydraulic lining-ground interaction of subsea tunnels[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(S2):3674 -3681.
[4] 蒋忠信.隧道工程与水环境的相互作用[J].岩石力学与工程学报,2005,24(1):121 -127.(JIANG Zhongxin.Interaction between tunnel engineering and water environment[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(1):121 -127.(in Chinese))
[5] Kolymbas,D P Wagner.Groundwater ingress to tunnels-The exact analytical solution[J].Tunnelling and Underground Space Technology Incorporating Trenchless Technology Research,2007,22(1):23 -27.
[6] S W Nam,A Bobet.Liner stresses in deep tunnels below the water table[J].Tunnelling and Underground Space Technology Incorporating Trenchless Technology Research,2006,21(6):626 -635.
[7] Mashimo,H,T Ishimura.Evaluation of the load on shield tunnel lining in gravel[J].Tunnelling and Underground Space Technology Incorporating Trenchless Technology Research,2003,18(2/3):233 -241.
[8] Lee I M,S W Nam.The study of seepage forces acting on the tunnel lining and tunnel face in shallow tunnels[J].Tunnelling and Underground Space Technology Incorporating Trenchless Technology Research,2001,16(1):31-40.
