多站无源时差定位精度分析

邢翠柳，陈建民

(中国电子科技集团公司第五十四研究所，河北石家庄050081)

0 引言

多站无源时差定位(TDOA)又称为双曲线定位，是一种重要的无源定位方式，是通过处理3个或更多观测站采集到的信号到达时间测量数据对辐射源进行定位的。在二维平面中，辐射源信号到达两观测站的时间差确定了1对以两站为焦点的双曲线，利用3站就可以确定2对双曲线来产生交点。若要确定三维空间中的任一辐射源，则至少需要4个站形成3对双曲线来产生交点，以确定辐射源的位置。当4个机载观测平台对运动目标进行三维时差定位时，其定位精度与时差测量误差、观测站站址误差和布站方式有关，针对不同的误差来源，采取相应措施达到提高目标定位精度的目的[1]。

1 定位原理

利用4个机载观测平台对运动目标进行三维定位，设定位系统中各观测站的空间位置为(xi，yi，zi)T，i=0，1，2，3 。其中，i=0 表示主站，i=1，2，3表示辅站。目标的空间位置为(x，y，z)T。

定位方程表示为:

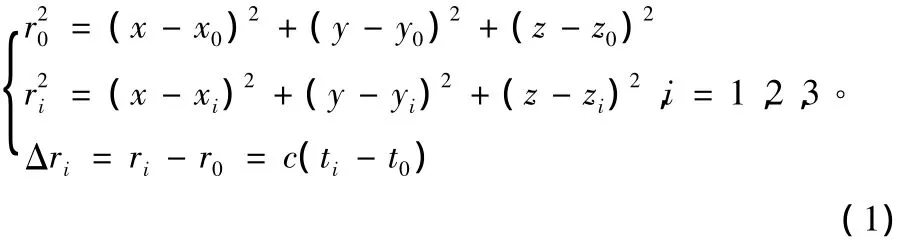
式中，ri为辐射源与第i站之间的距离;Δri为辐射源第i站与其到主站之间的距离差[2]。

根据误差传递原理，对 Δri=ri－r0(i=1，2，3)等号两边求微分，求得目标定位误差估计值:

式中，

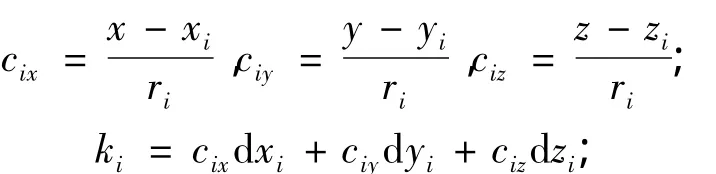
dX=[dx，dy，dz]T为目标定位误差;

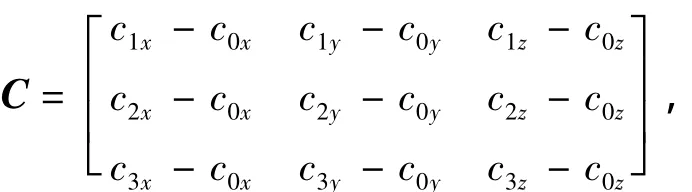
表明目标与各观测站的位置关系，与布站方式有关;dΔR=[d(Δr1)，d(Δr2)，d(Δr3)]T表示了各站到达时间差测量引入的误差;dXs=[k0－k1，k0－k2，k0－k3]T表示了由观测站站址测量引入的误差。

由以上公式可见，目标的定位精度与目标和各观测站的几何位置、站址误差和时差测量误差有关。

2 时差测量误差

时差测量误差主要来自接收机热噪声、多普勒测量误差、站间同步误差、信道时延、本地时钟误差和大气影响等[3，4]。

2.1 接收机热噪声

接收机热噪声的影响主要是使接收机产生随机误差，与接收信号的载噪比有密切关系。由接收机热噪声引起的随机误差为:

式中，T为信号积分时间;Δf为信号带宽;S/φ为信号与噪声谱密度比。在T=50 ms时，信号带宽为4*65 kHz的条件下，当S/φ约为50 dBHz时，热噪声引起的时差测量误差 σA约为12 ns;当S/φ为40 dBHz时，时差测量误差σA约为40 ns。

2.2 多普勒效应误差

由于目标与观测站之间存在相对运动，在进行时差测量时必然要考虑多普勒频率的存在对时差估计精度的影响。目标与观测站之间的相对位置，目标的飞行速度不断发生变化，导致多普勒频率和多普勒频率变化率实时变化，采取相应措施进行多普勒频差补偿后[5]，仍然会有多普勒频率残余量。假设真实多普勒频差为500 Hz，采用自相关法与互相关法相结合的多普勒频差估计方法进行多普勒频差补偿后，残余多普勒估计均值为0.000 4 Hz，均方差为0.002 1 Hz。

经过仿真验证可得，当采取相应措施进行多普勒频差补偿后，残余多普勒频差很小，基本可以忽略其对时延差估计精度的影响。

2.3 站间同步误差

当进行GPS单点时间传递时，卫星时钟误差、卫星星历误差和电离层、对流层延迟误差等对时间同步精度影响较大，这时若进行两观测站间的时间对比，有些误差还会被放大，无法满足高精度时间比对的要求，故采用GPS同源共视技术以消除或减弱各误差的影响。

采用GPS同源共视法对多个观测站进行时间同步时，由于同源共视法是观测同一颗卫星，卫星时钟钟差已经消除，电离层和对流层延迟已是两站的延迟之差，当两观测站相距不远时，可以近似认为两站的电离层和对流层延迟相等，这样电离层和对流层的影响基本可以消除，这时信号传播路径上的误差基本消除，在进行同源共视时间传递时，要求两观测站所用的接收机类型、天线长度和数据处理软件等都必须相同，尽量减小这一部分误差，剩余误差主要是由于卫星和接收机位置不准确引起的[6]。

对于同源共视后的卫星星历误差为:

式中，D为两观测站的距离;R为观测站到卫星的距离;σ1为GPS单点时间传递中卫星坐标的均方差。由于GPS卫星轨道高度为20 183 km，两观测站相距几十千米，卫星星历误差对时差测量误差的影响大大减小了。

对于同源共视后的接收机位置误差为:

式中，σ2为GPS单点时间传递中观测站坐标的均方差。在GPS同源共视时间对比中，接收机位置误差对时差测量误差的影响扩大了倍。因此，接收机位置误差将成为影响同源共视时间对比精度的重要误差源。

目前，在没有精密测定GPS接收机位置坐标的情况下，时差测量误差σC为30 ns左右。

2.4 信道时延

信道时延影响主要来自接收机滤波器的群时延变化，往往带宽越窄，群时延越大。但绝对时延属于系统误差，可以通过标校修订;但时延变化是随机的，将影响系统的测距精度，根据现有的工程技术水平，一个接收机的信道时延变化约为:σD=5 ns。

2.5 本地时钟误差

无源定位系统要实现ns级的高精度时间测量，必须要有秒以下的高精度的数字钟。由于GPS接收机只能提供秒以上的时间信息，因此，秒以下的数字钟要采用本地时钟，然后利用GPS接收机送出的1 PPS脉冲信号同步本地秒以下的时钟，实现高精度时间测量。当秒以下的时钟采用200 MHz晶振时，观测站本地时钟量化误差为5 ns。本地时钟误差还包括本地秒以下时钟的不准确和不稳定引起的误差，它在1 PPS信号到来之前会不断积累，因此需要高准确度和高稳定度的晶振，本系统采用铷原子钟，其稳定度为1×10－12，在1 s内造成的时差约为1×10－12×1 s，相对于其他误差源，对时差测量的影响可以忽略不计，因此，本地时钟误差σE=5 ns。

2.6 大气影响

大气是不均匀介质，当电波在大气中传播时，大气介质会使电波产生折射效应，以致传播速度小于光速，传播路径产生弯曲。

当目标飞行高度较低时，不存在电离层延迟，大气延迟主要是对流层延迟，对流层大气折射模型为:

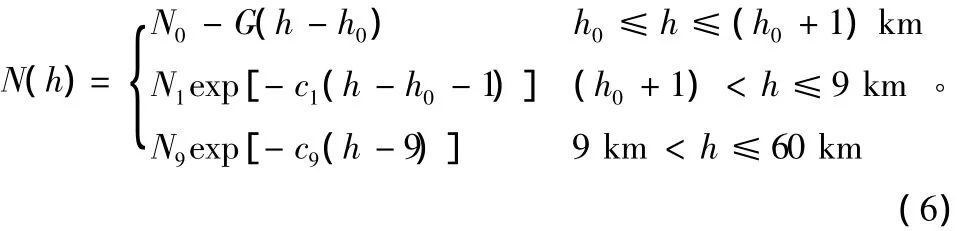
式中，N(h)为制定海拔高度上的大气折射率(N);h为指定海拔高度 (km);h0为地面海拔高度 (km);N0为地面大气折射率(N);N1为地面以上1 km高度处的折射率(N);N9为海拔9 km高度处的折射率(N);c1为地面以上1 km至海拔9 km大气层的指数衰减系数 (km－1);c9为海拔9 km高度以上的大气层的指数衰减系数 (km－1);G为近地面的折射率梯度，即dN(h)/dh。由

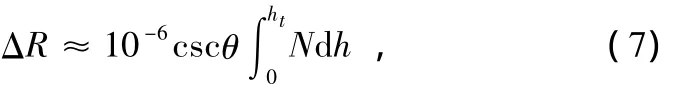
计算两观测站由大气对流层造成的时延值，假设目标相对于两观测站的俯仰角分别为θ1、θ2，在本系统中需要观测目标到两观测站的时延差，则影响时差测量误差的因素为两观测站的大气折射误差之差。

选取一组观测数据:h0=1;h0＜h＜39 km;N0=317.4;N1=274.3;N9=105.9;G=43.2;c1=0.120 6;c9=0.143 4;cscθ1=2.025 6;cscθ2=3.666 6。计算得到的两观测站的大气折射误差之差σF=12.8 ns。

2.7 总误差分析

综上所述，在多站无源时差定位中总的时差测量误差为:

若 σA=15 ns，σB=0 ns，σC=30 ns，σD=5 ns，σE=5 ns，σF=15 ns，则σ为30 ns，等效测距精度为9 m。

3 站址误差

由于在最终的目标解算中，观测站位置坐标已知，所以观测站位置坐标误差将直接导致定位误差。另外，该误差的影响大小还与定位解算的算法有关。由于本系统所设置的观测站为直升机平台，观测站的机动性导致观测站位置坐标误差较大。当观测信号长度为50 ms时，若直升机平台的运动速度为15 m/s，由此产生的站址误差为0.75 m。GPS接收机给出的站址信息存在的定位误差在米量级，综合2个误差来源，留有一定的误差余量，总的站址误差在5 m左右。

4 定位精度仿真结果分析

4.1 定位精度仿真

由定位原理分析可得，目标的定位精度受到时差测量误差站址误差和站址布局方式的影响。在该系统中，4架直升机观测平台布局方式如图1所示，采用平行四边形布站，通过matlab软件仿真在190 km×110 km范围内，4个观测站在观测范围内的位置分别为 (70 km，75 km)、 (150 km，75 km)、 (35 km，40 km)、 (120 km，40 km)，目标高度值为10 km时，在时差测量误差为30 ns，站址误差为5 m的条件下目标的定位误差[7]，仿真结果如图2所示，单位为m。由图2可得，越靠近4个观测站布局中心的位置目标定位精度越高。

图1 4架直升机平台的布站方式

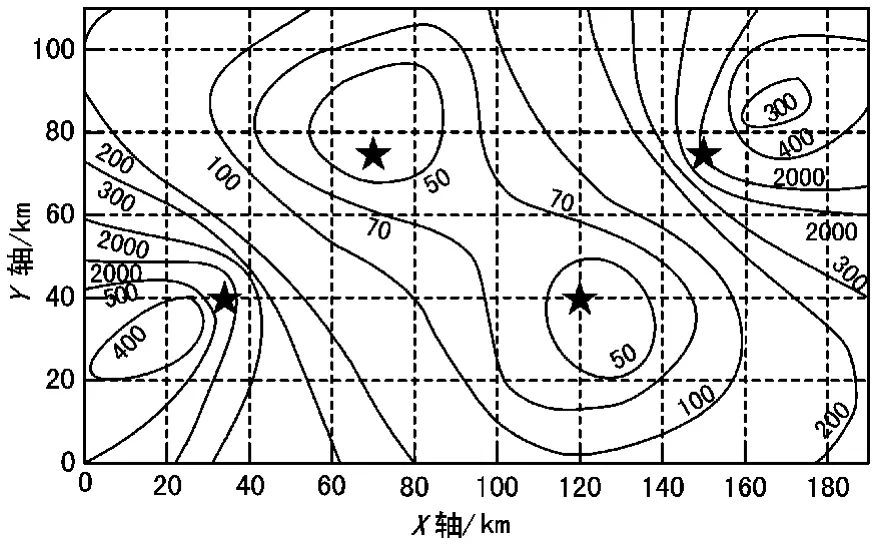
图2 目标的定位精度GDOP分布

4.2 提高定位精度的措施

从上述对定位精度的分析可以得到，在时差测量中主要的误差来源是接收机热噪声、多普勒效应和站间同步误差，对于多普勒效应误差，可以通过高精度的多普勒频差补偿来减小对时差测量精度的影响，而站间同步误差的主要影响因素是GPS接收机的位置误差。其次，在时差测量精度一定的情况下，观测站站址误差和布站方式对目标定位精度的影响也很大[8]。针对站址误差对定位精度的影响，采取精密测定观测站站址方法达到直接有效的改善目标定位精度的目的。

5 结束语

通过上述分析可知，接收机热噪声、观测站间的时间同步误差和多普勒效应是时差测量误差的主要来源。因此，高精度的时间同步技术是多站无源时差定位中的关键技术之一，基于频差补偿的时延估计方法可以明显改善多普勒效应对时延差估计精度的影响。同时，精密测定观测站站址位置和实现最优布站也对最终的目标定位精度有很大影响。

[1]胡来招.无源定位[M].北京:国防工业出版社，2004.

[2]王 玲.无源定位技术研究[D].吉林:长春理工大学，2008:24－29.

[3]谢 楠.多站时差定位精度分析[J].信息与电子工程，2003，1(3):38 －41.

[4]谢 楠.基于3Δt无源定位的再入低高度目标定位误差研究[J].电讯技术，2000(5):31－34.

[5]杨 艳.应用于卫星跟踪的VLBI软件相关处理关键技术的研究[D].上海:中国科学院上海天文台，2006:26－29.

[6]谢 楠.3Δt定位原理和定位误差研究[D].绵阳:中国工程物理研究院，2000:20－39.

[7]廖海军.多站无源定位精度分析及相关技术研究[D].西安:西安电子科技大学，2008:17－32.

[8]黄金凤，韩 焱，王黎明.无源时差定位布站方式对定位精度的影响[J].火力与指挥控制，2009，34(10):33－35.