基于CURE算法的电子装备时变误差分析

刘明辉，周 磊，谢婷婷，霍烁烁

(中国人民解放军63891部队，河南洛阳471003)

0 引言

电子装备试验的目的主要是对电子装备的各项战技指标进行考核。传统意义上的试验仅仅是对电子装备各项性能满足指标的程度进行考核，而并不过分关注装备本身指标性能可以达到的程度，这对装备性能的提升，缺陷的查找、分析和改进都是不利的。因此，有必要在试验过程中将装备试验数据与指标进行对照检验后，再进行进一步的分析，寻找其中的规律和问题。

在试验数据分析中，聚类分析是一类常见的试验数据处理方法，在试验数据分选、异常处理和故障判别等领域都有着广泛的应用。在各种聚类分析方法中，层次聚类方法是一种应用较为广泛的方法，典型的层次聚类算法有BIRCH算法[1]、CHAMELEON算法[2]和 CURE 算法[3]等。

CURE聚类方法是一种较为新颖的层次聚类方法，将传统算法对簇的表示方法进行了改进，提出了采用簇内多个数据点来代表簇的思想，从每个簇中抽取固定数量，分布较好的点作为描述该簇的代表点，代替类簇对象进行类簇之间的距离计算。通过迭代计算，将最相似的簇进行合并，以此完成聚类的目的。对于CURE算法，当前在国内已经有一些研究和成功的应用，如利用CURE算法进行网络用户行为分析[4]、相似重复记录检测[5]、通信异常检测[6]以及交通服务系统应用[7]等。

1 电子装备试验中的时变误差分析

在当前的电子装备试验模式中，其试验数据处理方法大多是基于经典统计学假设的，认为在试验过程中，试验数据满足平稳随机过程条件，在不同时间点获取的试验数据均满足同一分布，不受时间影响。然而，对于外场试验来说，由于试验环境、试验条件和试验手段的限制，其试验过程必然要受到各种因素的影响，在某些恶劣条件下，如高动态升空平台试验，其过程很可能是非平稳的，试验数据中包含了大量时变误差，如试验数据误差存在随时间跳变现象;或者试验数据误差存在时域周期性变化现象;或者验数据误差存在递增和归零现象等。形成上述时变误差的原因有很多，其原因可能主要有以下几点:①试验过程中各种干扰的影响，包括各种外部电磁环境影响，系统内设备的自扰以及测量设备与被试设备的互扰等;②被试设备和测量设备状态随时间的漂移，使得试验结果在一定范围内出现规律性变化;③被试设备本身的设计缺陷造成的影响。对于这类误差的分析、补偿和修正，是试验数据处理中面临的一项难题。为了更好地描述装备的指标特性，有必要寻找一种时变误差的处理方法来进行试验数据分析和处理。

2 基于CURE算法的时变误差处理方法

2.1 基于聚类的时变误差处理方法

对于存在时变误差的试验过程，可以对其误差状态空间做如下合理假设:

假设1:被试装备的误差状态空间是封闭的，并且总可以被划分为有限的若干区间类;

假设2:被试装备误差状态区间类之间相互独立。

根据以上假设，可以采用一种按时间分段处理的方法，将整个试验时段T划分为若干独立时间段，即T={t1t2…tn}，因为在较短的一个时段内，可以近似地认为，系统的状态是稳定的，其误差以短时随机误差为主。

由上述分析可得，对于电子装备时变误差的处理问题，最终可以归结为一个电子装备时变误差的聚类分析问题。经过研究，本文最终选取了CURE算法来进行时变数据的分类。

2.2 CURE聚类算法基本思路和步骤

CURE聚类算法是一种高效的聚类算法，采用代表点来描述簇，其算法基本思路是:首先把每个数据点作为不同的簇，然后不断使用基于代表点的方法对最相似的2个簇进行合并。CURE算法使用多代表点来描述簇的方法具有很多优点:①基于多代表点的簇间相似性度量既可以降低噪声点对簇合并的影响，又可以使相似性度量反映出簇的形状、分布等信息，因此得到的簇的质量更好;②在计算基于代表点的簇间相似度时，只需计算代表点之间的距离，而不需要计算簇内所有数据点之间的距离，因此算法效率更高。

CURE算法的详细描述如下:设数据集合Φ由n个数据点构成，即 Φ= { φ1φ2… φn}，C为簇集合，C={C1C2…Cn}，R(Ci)为簇Ci的代表点集合R(Ci)={ri1ri2…rip}(p＜λ)其中 λ为每个簇中的最大代表点数，收缩因子为α，定义dist(φ1，φ2)为任意2个数据项之间的欧氏距离，则2个聚类之间的距离为:

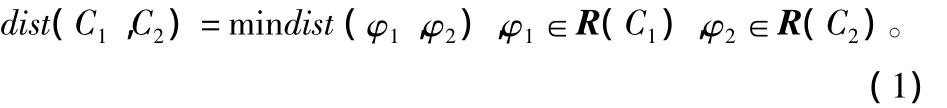
算法步骤如下:

① 根据每一个数据点 φi建立一个簇Ci，R(Ci)= φi。

② 找出簇集C中代表点最近的2个簇Cj，Ck。

③ 将簇Cj，Ck合并为新簇Cnew。

④计算新簇的质心

式中，表示簇中的样本数。

⑤ 构 建临时集合tempΦ，从新簇中选择 φi，如果tempΦ为空集，则使得φi满足条件:

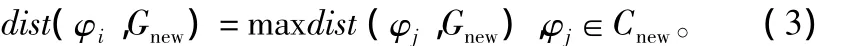
否则使得φi满足条件:

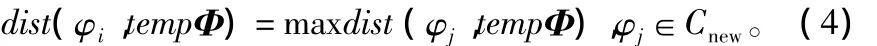
最后将φi并入tempΦ，如果tempΦ中元素个数大于λ，则终止步骤⑤。

⑥计算新簇Cnew的代表点:

⑦更新簇集，重新计算各簇间的距离dist(C1，C2)，重新执行步骤②。

对于算法终止的条件，可以采用文献[8]中的方法来判别。

定义1 类内距:类内两两不相同样本点之间的距离的平均，如果类内所有样本均相同，则类内距定义为0，类内距反映了类内样本的紧密程度。

定义2 类间连接对:若类i中距离样本点xj最近的样本点为xi，且类j中距离xi最近的点也为xj，则称(xi，xj)为类i和类j之间的1个连接对。其中xi属于类i，xj属于类j。

定义3 类间距:类i和类j之间的所有连接对的距离平均，类间距反映了类间分离程度。

由上述定义可得，如果类间距大于类内距，就会认为这2类不应该合并为1类，相反地，就会认为二者应该归为1类，在每次更新簇集后，计算一下各类的类内距和类间距，当所有类不应再聚合时，算法停止。

2.3 电子装备时变误差评价指标的选取

在成功完成误差状态空间分类之后，即可采用各种指标对电子装备系统的时变误差进行综合评价。对于装备误差的评价指标，通常情况下为系统的均值和方差，以及由均值和方差衍生出的CEP、中间偏差或者其他类指标，对于电子装备的时变误差，采用这些指标进行考核是不合适的，因此，本文提出了3种用于考核电子装备时变误差的指标，这些指标具有一定的代表性。

2.3.1 时变稳定度

设被试装备系统误差均值为μ，方差为σ2，其各时段误差的均值为E={μ1μ2… μn}，pk为各时段数据点数量与试验数据总量的比值，即pk=nk/N，则可定义系统的时变稳定度为:

时变稳定度描述了各时段误差均值与系统总体均值的偏离程度，ST值越小，则系统各时段的偏差值越小，系统性能越高。

2.3.2 时变一致性

设系统各时段方差为D={σ22… σ2n}，则系统的时变一致性可定义为:

式中，pk定义同上。

时变一致性描述了系统在存在时变误差条件下，在较短的时段内系统误差的一致性程度，也即被试装备系统短时的稳定程度，CT值越小，系统的时变一致性越好。

2.3.3 精度—时间概率

由于时变误差的存在，系统的精度实际上是一个变化量，在不同时间段，系统的精度是不同的，同理，对于某一确定的精度值，系统能够满足其要求的时间也是不同的。精度—时间概率定义如下:

设某一任务对系统精度需求为P，则系统的精度—时间概率为:

式中，tk为满足精度需求的时段;T为总时间。

3 典型算例

为验证该方法的有效性，这里采用仿真数据进行了验证，仿真数据源自2个不同型号的激光测距装备试验，采用线性变换的方式对试验数据进行了处理。两型装备的试验数据如图1和图2所示。

图1和图2描述了A、B不同厂家设计的一激光测距装备的误差分布，由图可以看出，A厂设计的激光测距装备误差较为均匀，而B厂设计的激光测距装备则表现出了较为明显的误差时变性。采用CURE算法对两型装备进行分类，最终A厂装备试验数据被分为1类，而B厂装备试验数据被分为5类，具体分类及数据结果如表1所示。由表1可以看出，A型装备误差均值小于B型装备，但方差大于B型，二者差别不大，对于误差均值和方差，二者不存在显著性差别(t检验，P＞0.05)。

图1 A型装备误差分布

图2 B型装备误差分布

表1 两型激光测距装备数据误差及分类结果

但若对时变误差进行考虑，计算两型装备的时变稳定度、时变一致性及精度—时间概率(精度p≤3 m)指标，则可发现两型装备的明显差别，具体计算结果如表2所示，其中试验点数为100。

表2 两型激光测距装备时变误差分析结果

由表2可知，A型装备的时变稳定性较好，误差分布较为均匀，一般情况下应优先选用A型设备;但B型装备时变一致性较好，若系统中还存在其他设备进行修正或者有条件采用差分方法，则B型设备可以提供更高的精度;对于某些指定精度(如要求精度≤3 m)的任务需求，采用A型装备是一个较好的选择。

4 结束语

在以往的试验过程中，对电子装备的时变误差考虑较少，因此对系统的评价存在一定的片面性。本文提出了一种基于CURE算法的电子装备时变误差分析处理方法，通过CURE算法对试验数据进行聚类，采用时变稳定度、时变一致性和精度—时间概率对被试装备的时变误差进行了考核，考核结果对装备的评价、选型和改进都有一定的指导意义，本文所提出的方法，也可以推广到其他应用领域中，具有较为广泛的应用前景。

[1]ZHANG T，RAMAKRISHMAN R，LIVNY M.BIRCH:An Efficient Data Clustering Method for very Large Databases[C].In Proc.1996 ACM-SIGMOD Int.Conf.Management of Data.Canada，1996，1 032-1 141.

[2]KARYPIS G，HAN E H，KUMAR V.CHAMELEMON:Ahierarchical Clustering Algorithm Using Dynamic Modeling[J].COMPUTR，1999(32):682 －751.

[3]GUHA S，RASTOGI R，SHIM K.CURE:an Efficient Clustering Algorithm for Large Database[J].Information Systems，2001，26(1):35 －58.

[4]孙燕花，李 杰 ，李 建.基于CURE算法的网络用户行为分析[J].计算机技术与发展，2011，21(9):35－38.

[5]时念云，张金明，褚 希.基于CURE算法的相似重复记录检测[J].计算机工程，2009，35(5):56－58.

[6]周亚建，徐晨，李继国.基于改进CURE聚类算法的无监督异常检测方法[J].通信学报，2010，31(7):18－23.

[7]张 愚 ，翁小雄.CURE聚类方法及其在交通服务信息系统中的应用[J].科学技术与工程，2009，9(10):2 611－2 615.

[8]向 娴 ，汤建龙.基于改进的支持向量聚类的雷达信号分选[J].航天电子对抗，2011，27(1):50－53.