三排微型桩内力分布的数值模拟
2012-06-13辛建平郑颖人唐晓松覃小华孙露
辛建平,郑颖人,唐晓松,覃小华,孙露
(1后勤工程学院军事建筑工程系,重庆401311;2岩土力学与地质环境保护重庆市重点实验室,重庆401311;3军事医科学院院务部,北京100850)
0 引言
微型桩,一般指直径小于300mm的钻孔加筋灌注桩,常以群桩的形式工作。微型桩作为一种新型抗滑结构,以其常规抗滑桩不能替代的优点在边坡加固和滑坡治理尤其是一些应急抢修工程中都得到了越来越广泛的应用,但目前对于微型桩的抗滑机制与破坏机理尚缺乏系统全面的认识,也没有成熟的计算方法,理论滞后于实际应用[1-7]。
现有的微型桩数值模拟、理论计算模型对桩体均采用线弹性本构模型,而实际上由于微型桩桩径小,长径比大,钢筋量少,抗弯刚度很低,受力后很容易发生塑性变形,因而,我们认为微型桩必将进入塑性,且在滑带处发生破坏,坡体的破坏是沿着滑面进行,所以在进行边坡稳定性分析时桩体应按弹塑性理论进行计算,尤其在应急抢修工程中允许桩体进入塑性状态并发生较大变形,这并不影响工程使用,只要其仍可发挥抗滑作用并保证坡体不垮塌便可满足要求。此外,桩体进入塑性状态能够使材料的力学性能得到充分发挥。为此,我们在边坡稳定性分析时把岩土与微型桩都按弹塑性材料,采用有限元极限分析方法进稳定性评价,然后使用结构单元来得出其破坏前在不同滑坡推力下的内力变化规律,为微型桩优化设计提供思路。
1 计算模型
1.1 模型的建立
1.1.1 单元属性及本构模型
利用FLAC3D软件建立三维模型,岩土体采用摩尔-库仑(Morh-Coulomb)理想弹塑性本构模型,当桩体采用结构单元时选用程序自带的pile单元模拟桩体,beam单元模拟连系梁;当桩体的混凝土和钢筋均采用实体单元时,本构模型也均采用摩尔-库仑(Morh-Coulomb)理想弹塑性本构模型,其中钢筋的c值去其抗剪强度,摩擦角取0,相当于钢筋采用了屈雷斯卡(Tresca)模型。
坡体高36.5m,长75m,宽度方向取1m范围进行建模。人为设置一折线形滑带,厚0.5m。桩长17.5m,嵌固段为6.5m,横、纵桩间距均取3.3倍桩径,顶部采用40cm×40cm×230cm混凝土连系梁将3根桩进行加固,第二排桩布置在37.5m处,桩体编号从左到右依次为2号、1号、3号。桩体采用实体单元时,取圆形截面,桩心配筋,桩径30cm,钢筋采用3C32,建模时将其等效为1根直径54.4mm的钢筋。图1为模型的纵截面图,图2为桩体采用实体单元时模型布桩位置的横截面图及网格划分,中间的圆形网格代表桩体,黑色圆点部分为钢筋。
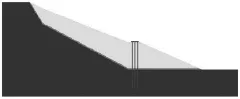
图1 模型切面图
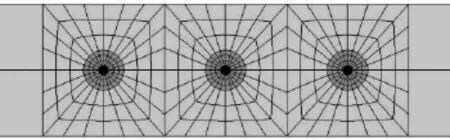
图2 布桩位置坡体横截面图
1.1.3 边界条件
模型上部为自由边界;底面(Z=0)为位移约束边界,约束垂直方向的位移;两侧(Y=0,Y=1)和前后(X=0,X=75)也为位移约束,约束水平方向位移。
1.2 材料参数
FLAC3D计算中需要输入的材料力学参数是体积模量(K)、剪切模量(G),因此根据FLAC3D提供的力学公式进行换算:
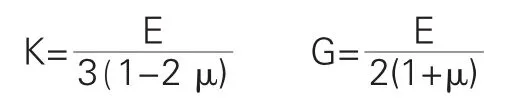
本文中混凝土的c、φ值采用目前应用较多的由混凝土轴心抗压强度和抗拉强度换算得到的值,即联立求解下列两个方程得出:
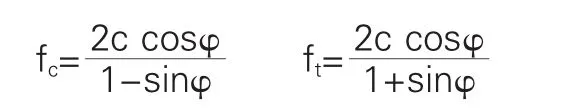
式中fc、ft分别为混凝土轴心抗压强度标准值和轴心抗拉强度标准值。
严格来说,混凝土的c、φ值应按试验求得。一般来说,与上述计算方法得到的值相比,试验得到的c值较大,而φ值较小。表1为材料的力学参数,分别为弹性模量、泊松比、体积模量、剪切模量、黏聚力、摩擦角和抗拉强度。
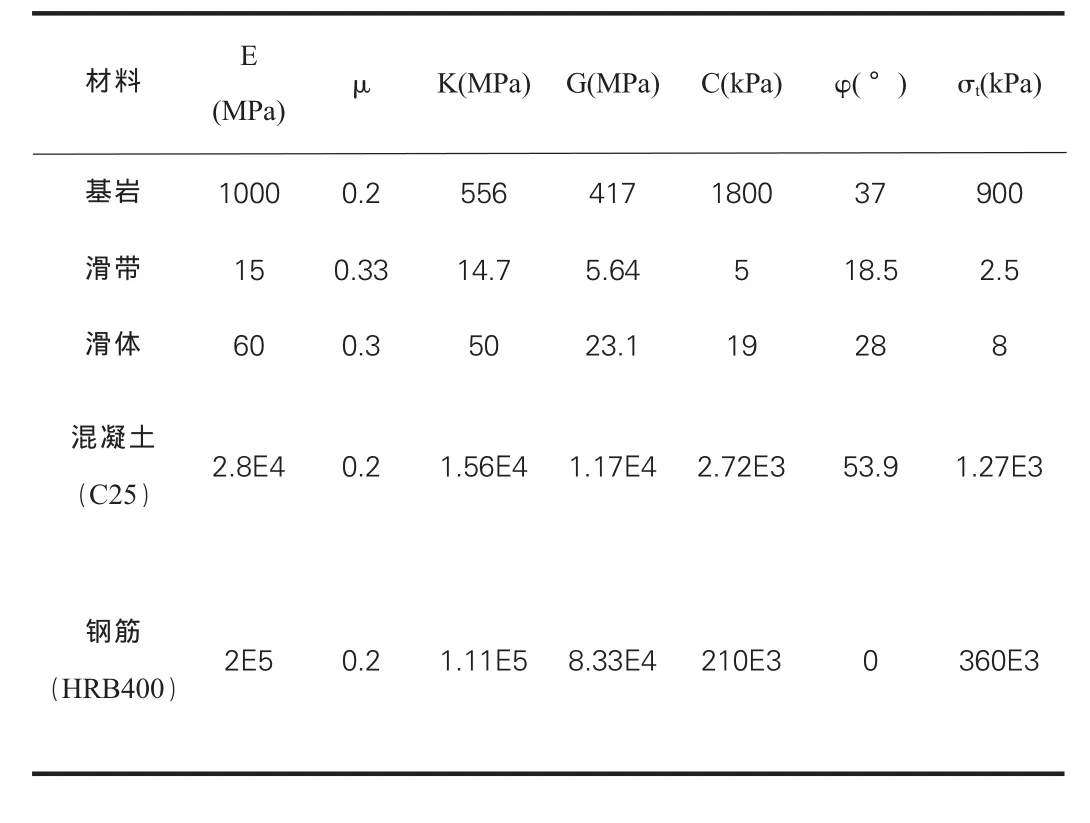
表1 材料力学参数表
2 有限元强度折减法原理
有限元强度折减法是有限元、有限差分、离散元等强度折减法的统称。本文实际应用FLAC有限差分强度折减法,分析了土质边坡工程中施桩后的边坡稳定安全系数和桩体内力分布。
像微型小说《启程》中表达的那样,在卡夫卡的世界里,人的诞生就是一种“出发”[14]402,而人生是一条漫长的路,一次通向未知的旅行。在这条路上,人找不到值得为之奋斗的目标,人生只能是不断重复的“出发”,为了努力奔向无可预知的远方,直到死亡将其终结。我们身外的世界是没有意义的,我们甚至不能通过对外在的行动的选择来确定自我存在的意义。“目标只有一个,道路却无一条”[15]219,“向死而生”成了卡夫卡小说人物普遍选择的一种结局。和《等待戈多》式的“虚无”的等待中所隐含的希望不同的是,卡夫卡笔下的生存虚无是一种更加彻底的东西。
目前有限元强度折减法在边坡的静力稳定性分析中已经相当成熟[8-10]。因为静力情况下边坡主要是受到剪切破坏,所以静力下的有限元强度折减法是将边坡体的抗剪强度指标c和tanφ分别折减ω,折减为c/ω和tanφ/ω,使边坡达到极限破坏状态,此时边坡的折减系数即为边坡的稳定系数[11]。
本文在分析边坡稳定性及桩体破坏时既考虑了剪切破坏也考虑了拉破坏,所以在应用有限元强度折减法的时候,同时考虑折减岩土体黏聚力c,内摩擦角φ,以及抗拉强度σt,即
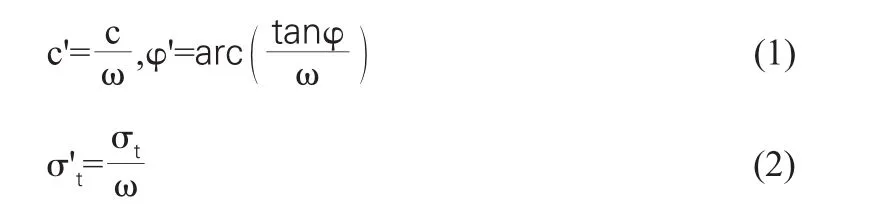
式中c',φ',σ't分别为折减后的岩土体黏聚力,内摩擦角和抗拉强度,ω为折减系数。
3 破坏依据
3.1 有桩坡体破坏依据
静力条件下当采用有限元强度折减法进行计算时,判断边坡是否剪切破坏一般有3个条件[12-13]:(1)以塑性区或者等效塑性应变沿滑面贯通作为边坡整体失稳的标志;(2)以坡体内某特征点的位移发生突变作为标志;(3)以有限元静力平衡计算不收敛作为边坡整体失稳的标志。其中塑性区贯通只是必要条件而非充分条件。FLAC应用静力强度折减计算边坡的安全系数时采用计算不收敛作为边坡破坏的标志[14]。本文在判断坡体的破坏时是以坡体内塑性区贯通和计算不收敛作为主要依据,同时以特征点的位移发生突变作为验证。
3.2 特征点的布置
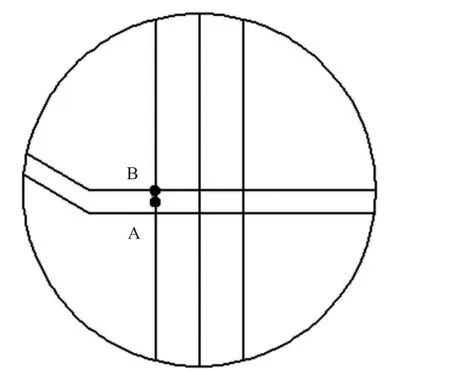
图3 特征点分布情况
在滑带处的第一排桩体钢筋单元上设两个特征点监测其位移情况,该处的破坏最具代表性。其坐标为A(46.6,0.5,10.75),B(46.6,0.5,11)。
4 坡体稳定性分析
考虑到微型桩易进入塑性状态发生滑带处的剪弯破坏,故对微型桩加固后的坡体进行稳定性评价时桩体采用实体单元进行模拟。根据前面所述的破坏判断依据,下面对三排微型桩加固的坡体进行稳定性评价。
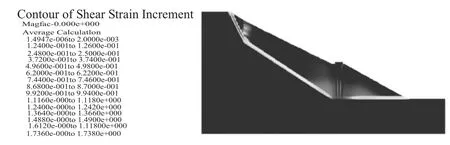
图4 ω=1.45时坡体的剪应变增量云图
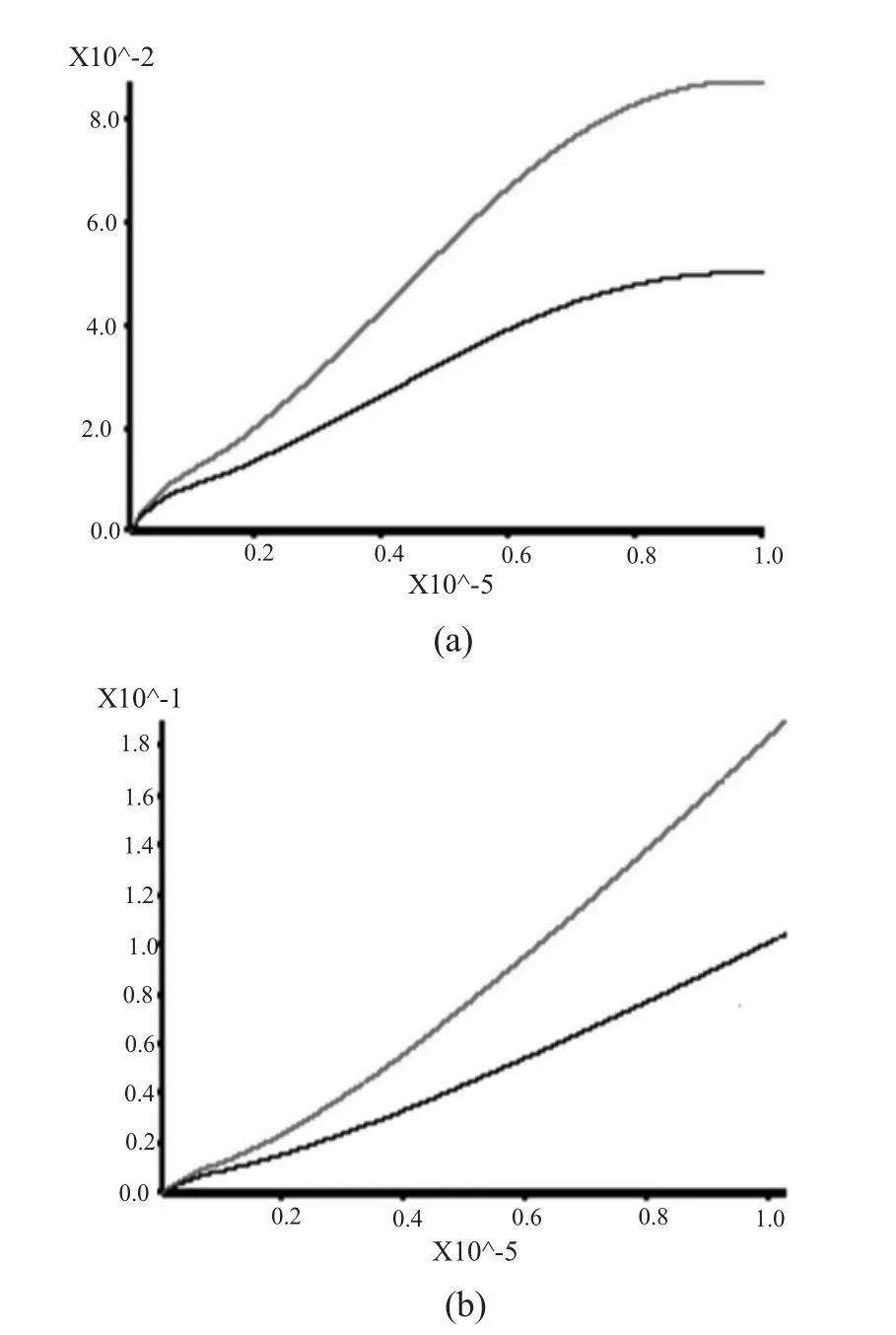
图5 特征点位移曲线图
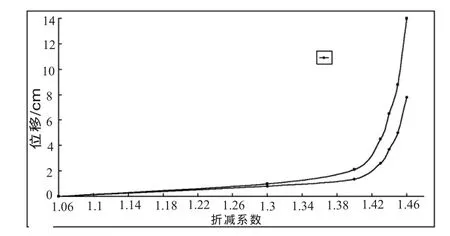
图6 特征点位移-折减系数曲线图
从图4剪应变增量云图来看,ω=1.45时滑面上的塑性区已经贯通,表明形成了贯通的破裂面。由特征点位移曲线图可知,ω=1.45时特征点B的最终位移为8.7cm,且保持水平,说明桩体的变形停止,边坡是稳定的;而ω=1.46时位移无趋于平缓的迹象,当计算到80万步时B点的横向位移已达14cm,计算不收敛,说明此时桩体已发生破坏,边坡失稳。同时由图6可以看出,随着折减系数的增大特征点位移也逐渐增大,ω=1.46时出现突变。因此,根据上述现象综合判断得到三排桩支护时的稳定系数定为1.45。
5 三排微型桩内力计算结果分析
通过FLAC有限差分强度折减法计算得到边坡的初始稳定系数为1.06,由前面的分析可知,加了三排微型桩后的坡体稳定性系数为1.45,表明三排微型桩具有良好的效果。下面采用结构单元模拟桩体,对桩体破坏失效前不同折减强度下的桩体内力分布及不同排间的最大内力分配进行分析。
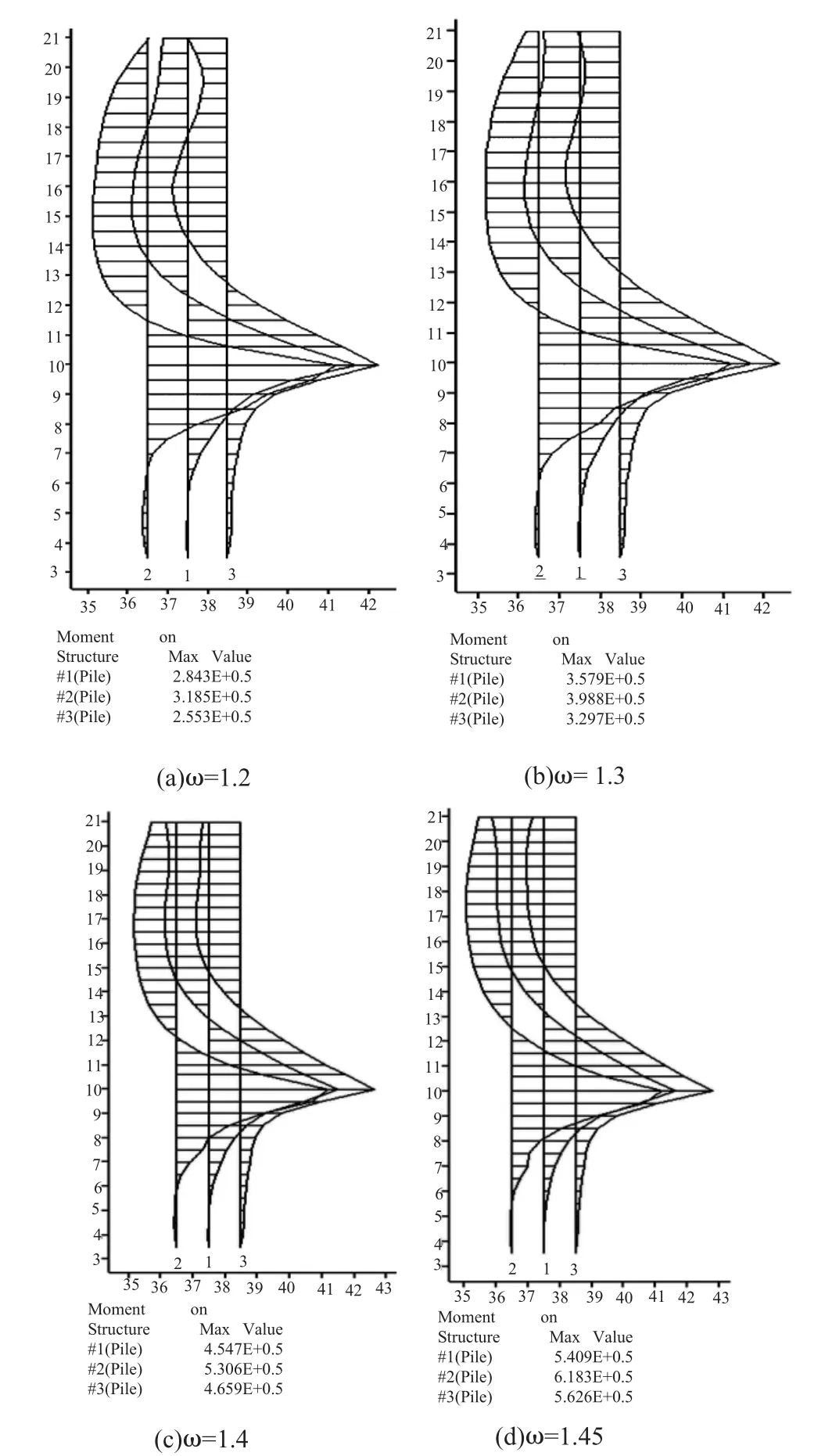
图7 不同折减系数下桩体弯矩分布图
5.1 不同折减强度下桩体弯矩分布
由图7中不同折减系数下的弯矩分布图可知,桩体所受最大弯矩均位于滑带下沿处(10m),滑带附近桩体的弯矩要大于桩体其他部位,变化比较剧烈,且随折减系数的增大有上移趋势。而桩体上三分之一部分所受弯矩大小比较均匀,桩体下端几乎不受弯矩。不同排间的桩体所受最大弯矩的分配并不是一成不变,由计算数据可以看出在ω=1.4之前,2号桩所受弯矩最大,1号桩次之,3号桩最小;当ω=1.4时发生变化,2号桩所受弯矩最大,3号桩次之,1号桩最小,ω=1.45时这种现象更加明显。说明不同排间桩体的弯矩大小分配是随着滑坡推力的大小发生变化的,滑坡推力较大、坡体接近破坏时第一排桩所受弯矩最大,第三排其次,第二排最小。
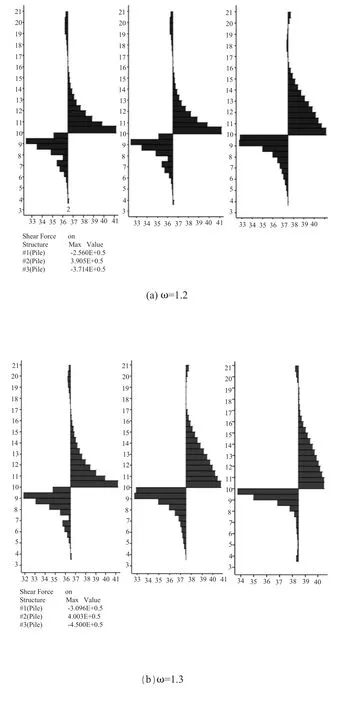
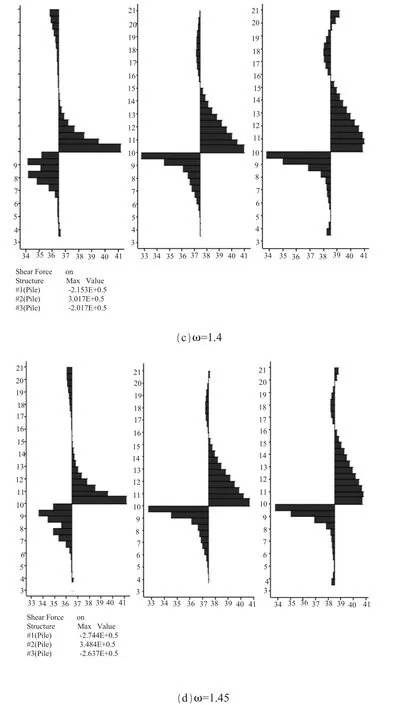
图8 不同折减系数下桩体剪力分布图
5.2 不同折减强度下桩体剪力分布
由图8可以看出桩体所受剪力主要分布在桩体中下部,最大值均位于滑带处,向两端依次减小;2号桩所受最大剪力方向与1号桩和3号桩相反,2号桩所受最大剪力位于滑带上方,而1号桩和3号桩所受最大剪力位于滑带下方;随着折减系数的增大,不同排间桩体的剪力也逐渐增大,但增加幅度并不一致,由计算结果可以看出在ω=1.4之前,最大剪力的分配为2号桩最大,1号桩其次,3号桩最小,当ω=1.4时变为2号桩最大,3号桩其次,1号桩最小,而当ω=1.45时3号桩最大,2号桩其次,1号桩最小。这说明不同排间最大剪力的分配是随着滑坡推力的大小发生变化的,虽不像弯矩变化那样规律,但滑坡推力较大、坡体接近破坏时第二排桩所受剪力一直是最小的。
6 结论
(1)依据微型桩的破坏特点提出对采用微型桩加固的坡体进行稳定性分析时桩体应采用弹塑性本构模型,同时考虑了坡体和桩体的破坏,给了三排微型桩坡体的稳定安全系数的计算方法。
(2)得到了具有纵向连系梁的三排桩心配筋微型桩的弯矩分布规律。单桩所受最大弯矩均位于滑带处,在本模型下不同排间最大弯矩的分配随着滑坡推力的增大发生变化,滑坡推力较小时,第一排桩所受弯矩最大,第二排其次,第三排最小,滑坡推力较大、坡体接近破坏时第一排桩所受弯矩最大,第三排其次,第二排最小。
(3)得到了具有纵向连系梁的三排桩心配筋微型桩的剪力分布规律。单桩所受最大剪力位于滑带处,在本模型下滑坡推力较小时,第一排桩所受剪力最大,第二排其次,第三排最小,滑坡推力较大、坡体接近破坏时靠边两排桩体所受剪力较大,第二排最小。
(4)为工程中微型桩优化设计提供思路,针对不同滑坡推力对各排微型桩可进行不同强度设计,对其滑带附近部位也可进行不同程度的加固。
[1]Brown Dan A,Shie Chinefeng.Numerical Experiments into Group Effects on the Response of Piles to Lateral Loading[J].Computers and Geotechnics,1990,(3):211-230.
[2]Sadek M,Shahrour I,,Mroueh H.Influence of Micro-Pile Inclination on the Performance of a Micro-Pile Network[J].Ground Improvement,2006,10(4):165-172.
[3]陈正,梅岭,梅国雄.柔性微型桩水平承载力数值模拟[J].岩土力学,2011,32(7):2219-2224.
[4]冯君,周德培,江南,等.微型桩体系加固顺层岩质边坡的内力计算模式 [J].岩石力学与工程学报,2006,25(2):284-288.
[5]阎金凯.滑坡微型桩防治技术大型物理模型试验研究[D].西安:长安大学,2010.
[6]刘凯.注浆微型钢管组合桩抗滑机制及计算方法研究[D].青岛:中国海洋大学,2010.
[7]郑颖人,赵尚毅,张鲁渝.用有限元强度折减法进行边坡稳定分析[J].中国工程科学,2002,4(10):57-62.
[8]赵尚毅,郑颖人,张玉芳.极限分析有限元法讲座Ⅱ——有限元强度折减法中边坡失稳的判据探讨[J].岩土力学,2005,26(2):332-336.
[9]赵尚毅,郑颖人,王建华,等.基于强度折减安全系数的边坡岩土侧压力计算方法探讨 [J].岩石力学与工程学报,2010,29(9):1760-1766.
[10]郑颖人,叶海林,黄润秋.地震边坡破坏机制及其破裂面的分析探讨 [J].岩石力学与工程学报,2009,28(8):1714-1722.
[11]郑颖人,肖强,叶海林,等.地震隧洞稳定性分析探讨[J].岩石力学与工程学报,2010,29(6):1081-1088.
[12]肖强,郑颖人,叶海林.静力无衬砌黄土隧洞稳定性探讨[J].地下空间与工程学报,2010,6(6):1136-1141.
[13]Itasca Consulting Group,Inc..Fast Lagrangian analysis of continua in three dimensions(version 3.0), users’ manual[R].[S l]:Itasca Consulting Group,Inc.,2003.
[14]ZHENG Y R,DEN C J,TANG X S,et al.Development of finite element limiting analysis method and its application in geotechnical engineering[J].Engineering Sciences,2007,3(5):10-36.
[15]ZHENG Y R, TANG X S,ZHAO S Y,et al.Strength reduction and step-loading finite element approaches in geotechnical engineering[J].Journal of Rock Mechanics and Geotechnical Engineering,2009,1(1):21-30.
