地震作用下预应力锚索抗震性能及预应力损失的研究

刘云 ，王成，郑颖人，赖杰

（1重庆交通大学土木工程学院，重庆400074；2重庆地质灾害防治工程技术研究中心，重庆400041；

3后勤工程学院军事建筑工程系，重庆401311）

0 引言

目前地壳较为活跃，地震不断、滑坡频繁，严重危害人类的生命财产安全。仅在我国的汶川地震诱发的滑坡多达1万多处，大量的滑坡使得公路铁路交通中断，更给救援工作带来了极大的困难，造成巨大的经济损失。滑坡造成的地质灾害损失占到整个地震损失的1/3左右。基于此，作者对预应力锚索在地震作用下的抗震性能与预应力损失进行了分析。文章采用摩尔-库伦屈服准则，利用可以考虑岩土体抗拉强度的FLAC3D软件进行数值模拟，初步探讨了锚索预应力损失随地震动作用过程的变化情况、支护边坡抗震性能，旨在为预应力锚索支护边坡的抗震性能分析与支护设计提供一定依据。

1 失稳破坏准则

在边坡动静力稳定性分析中，首先要弄清楚的是边坡的破坏机制，知道破裂面的位置和破裂面的性质（剪切破坏或张拉破坏）。目前，通常是假定边坡破坏就是剪切滑移破坏，通过极限平衡方法搜索边坡的最不稳定滑面，再通过积分运算求得抗滑力与下滑力的比值，从而得到边坡稳定系数，并以此评价边坡在静力条件下的稳定性，对于动力问题往往最终也是转化为静力问题进行求解。我国著名的地质学家谷德振从国内外众多工程实践分析指出：岩质体的失稳破坏主要由剪切滑移、拉张开裂破坏及压缩变形这三个方面引起[1]。文献[2]、[3]也指出岩体的变形破坏应随岩体的特征及受力状态的不同而有所差异，其主要的破坏机制可以分为剪切破坏和张拉破坏两大类。

简单的剪切破坏机制无法对一些现象进行合理地解释，比如：①在某些工况下，靠近坡顶的边缘附近，坡面的径向与坡顶面的切向应力的合力将为拉应力，在拉应力的作用下，坡顶一定深度内的部分土体将受拉破坏[4]；②汶川地震中滑坡滑体飞跃的现象；③地震时破裂面的破裂性质及位置。因此传统将边坡视为剪切滑移的分析方法不是考虑保守，造成浪费；要么安全因素思考不够全面，使边坡存在一定的危险[5]。基于此，本文利用完全动力有限元法[6,7]，该法不仅荷载是动力的，而且破裂面也是动力分析得到的，能考虑岩体的抗拉强度对稳定性的影响，能够较好地反映边坡的地震响应与抗震性能。采用的屈服准则为考虑岩体自身的抗拉强度的摩尔-库伦准则，该破坏准则写为下式：

其中：τf为土体的抗剪强度，σ3为第三主应力,σ1为岩体抗拉强度，φ为岩体内摩擦角，C为粘聚力，σ为法向应力。

2 数值模拟

本小节采用的数值模拟模型为一个坡高25m、坡角70o的Ⅲ类岩质边坡，开展预应力锚索抗震性能与预应力损失相关研究。该边坡位于8度抗震设防地区，岩体容重25.0 kN/m3，存在倾角45o的外倾软弱结构面。设置的四个监测点（A、B、C、D）位置如图1所示。边坡等级为二级，重要性系数为1.0。

边坡采用预应力锚索支护，横向间距2.5m，锚索竖向间距3m。每列设置6孔锚索，单孔锚索为3束，锚索极限承载力776kN，设计预应力为390kN，弹性模量为20GPa。锚索水平倾角均为20°，每孔锚索设计锚固段长5.0m，全部锚入基岩中，从上到下施加的预应力锚索编号为A1～A7，设四个监测点ABCD如图1所示。

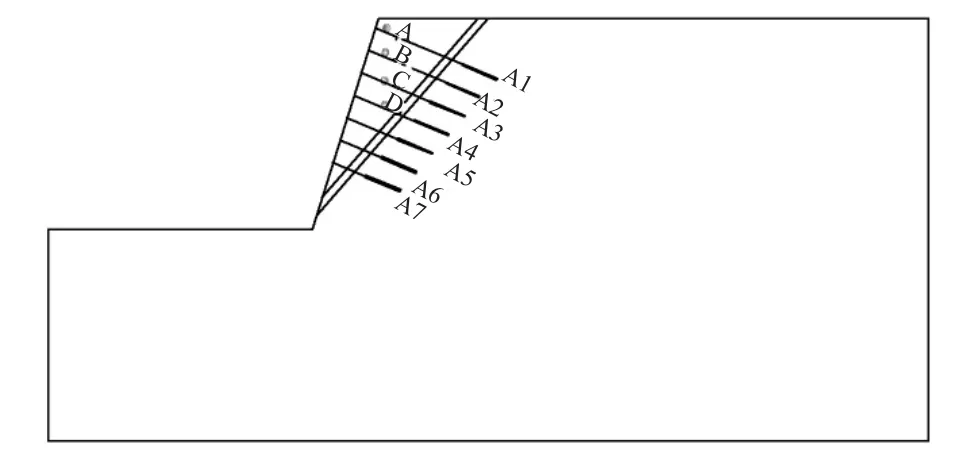
图1 预应力锚索支护边坡示意图

数值模拟时的材料视为理想弹塑性材料、利用FLAC3D软件[8]中的Cable单元模拟预应力锚索。边界条件采用自由场边界，阻尼采用局部阻尼，阻尼系数为0.15。边界大小应该计算的精度要求，本算例采用的计算边界为：坡脚到左端边界的距离为坡高的1.5倍，坡顶到右端边界的距离为坡高的2.5倍，上下边界总高为坡高2倍[9,10]。模型的材料参数情况如下表1所示。

表1 岩体物理力学参数

输入的地震波加速度都是经过过滤和基线校正处理的双向地震波。 波的类型有三类：EL Centro波(EL，1940年，NS向)、Linghe波(Linghe，1995年，NS向)和qiqi波(qiqi，1997年，NS向)，如图2所示。双向地震波的垂直向加速度峰值取水平向加速度峰值的2/3。为了考虑峰值大小对预应力锚索支护边坡抗震性能、预应力损失的影响，三种地震波峰值取0.1g、0.2g、0.4g，总的计算工况如表2所示。

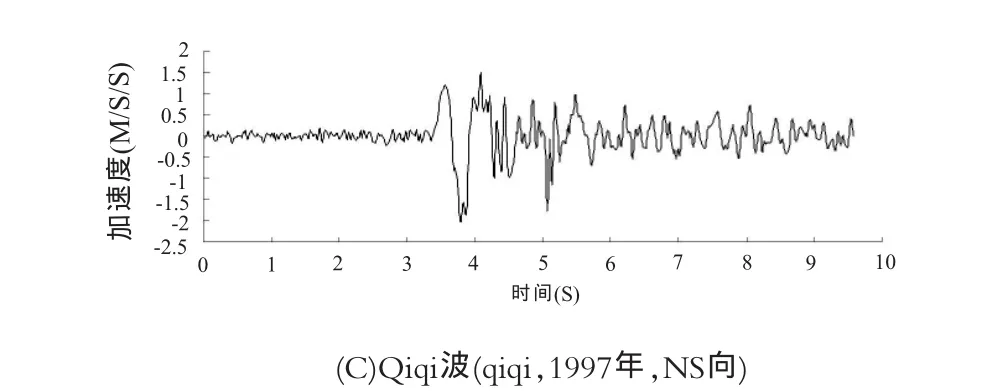
图2 计算输入的加速度曲线

表2 预应力锚索数值分析工况表

3 预应力锚索地震动下抗震性能与预应力损失分析

本节通过与没有锚索支护边坡响应监测点的地震响应进行对比，以此来能更好地反映预应力锚索支护边坡的抗震性能。因坡体的加速度响应能较好地反映边坡的动力特性，为了更清晰地体现监测点相应加速度增大的程度，将监测点响应水平地震波的峰值与实际输入的水平地震波的峰值之比定义为加速度PGA放大系数。按照规范规定不同的地震烈度对应不同的加速度峰值。

当输入的地震波峰值加速度为0.4g时，各监测点的加速度响应情况从图3可以看出：监测点位置越高加速放大系数越大，边坡的地震响应越明显，不同的地震波加速度响应不一样，EL Centro最为明显，Linghe波较弱，放大系数大约在1.5至4倍之间。其中，（a）部分（预应力锚杆支护）的监测点放大系数比（b）部分（无支护）对应的监测点加速度放大系数要小，表明前者能减弱地震对边坡的作用，起到一定的减震效果。

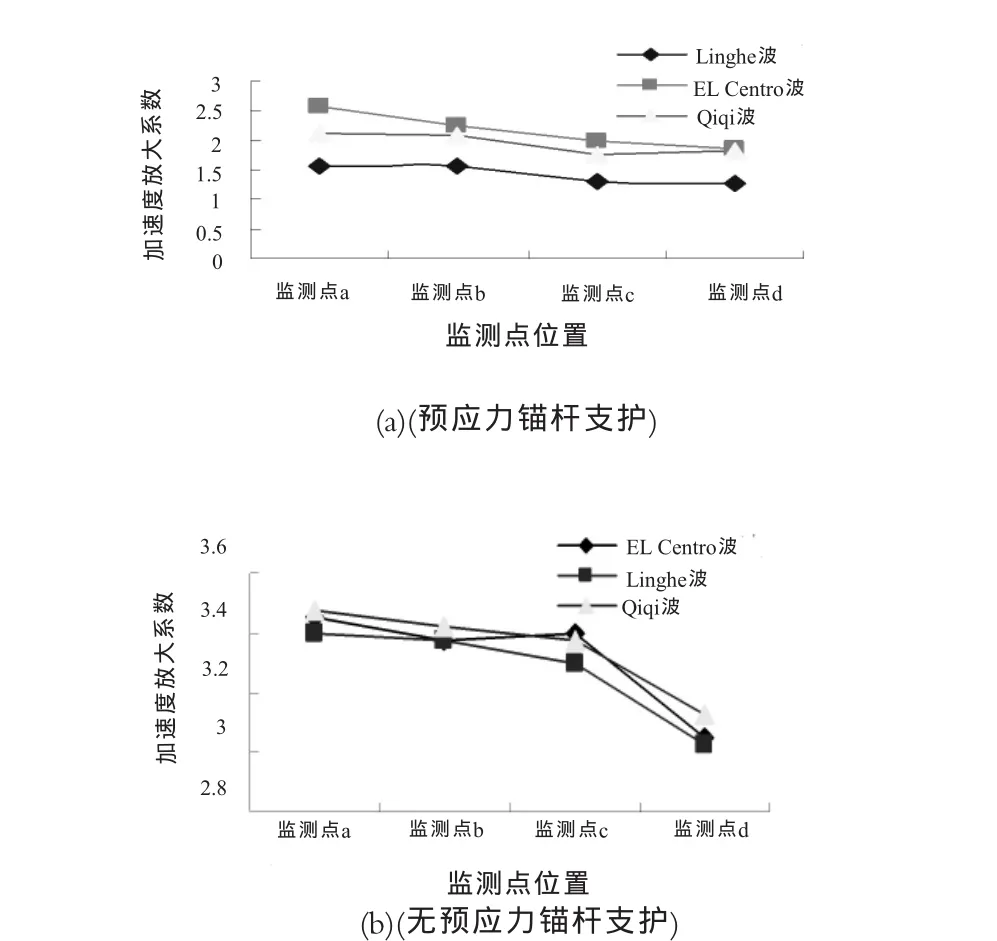
图3 监测点加速度放大系数

从图4可以看出，监测点越高水平位移越大，地震响应越明显，这与监测点越高，与其相应的加速度放大效应越大相一致（如图3所示）。有预应力锚索支护（a部分）比无支护时在地震下的位移要小很多，表明前者起到了很好的抗震作用。

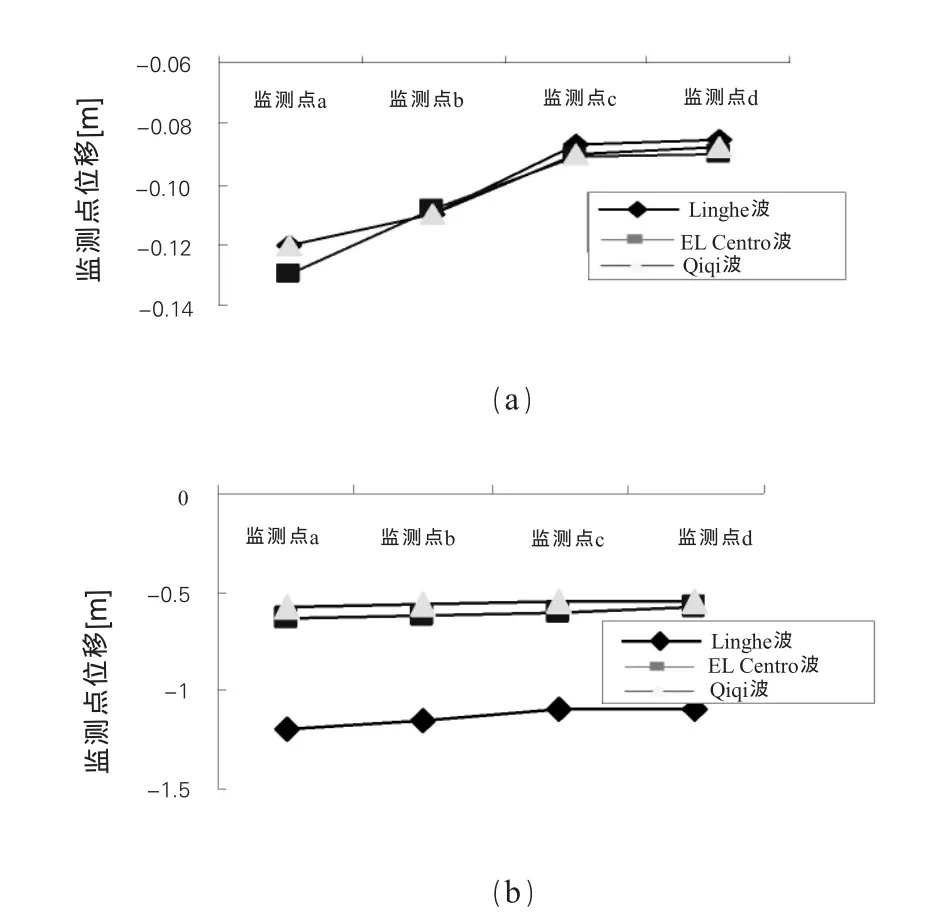
图4 各监测点的位移

图5描述的是输入地震波峰值为0.2g时，在三种地震波下锚索的预应力的变化情况，曲线从上到下依次对应A1～A5锚索预应力。从图中可以看出：在初始时刻预应力损失较为明显，约为初始应力的6%～17.9%，主要原因是加载时土体压缩造成的预应力损失，锚索在坡面的位置越高损失越小。随着地震动的进行，在地震波峰值时刻，锚索应力水平增长较快，在地震作用较小时，应力保持水平。地震完后各排锚索预应力损失如表3所示。在地震下靠近坡顶的锚索起到的抗震作用更大。

从表3可以看出，锚索预应力在不同的地震波作用下，预应力损失并不相同，本算例EL Centro波损失较大，Qiqi波损失较小。

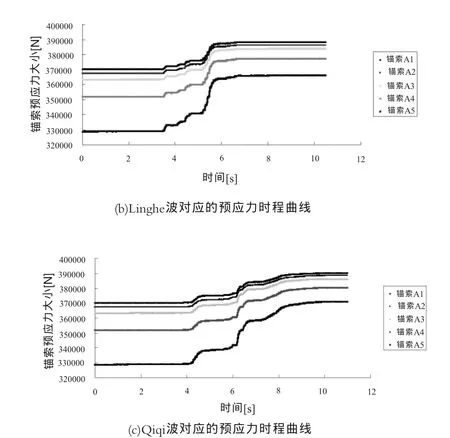
图5 锚索预应力时程曲线

表3 锚索预应力最终损失

4 结论

本文通过对比有预应力锚索支护边坡与没支护边坡在地震波作用下的动力响应，得到预应力锚索能较好地起到抗震作用的结论。利用锚索预应力时程曲线，分析在地震动作用下，各排锚索分担力的情况及最终预应力损失情况。主要结论有：

（1）预应力锚索能很好地减弱边坡体的加速度放大效应，起到较好减震效果。

（2）监测点越高，地震响应越明显，水平位移越大。相对于无支护边坡，预应力锚索支护边坡的监测点位移大约为前者8%。

（3）随着地震动的进行，锚索预应力在地震波峰值时刻后增长较快，在地震作用较小时，应力水平几乎不变。在地震下靠近坡顶的锚索起到的抗震作用更大。

（4）因监测点越高地震响应越明显，位置越高的锚索的应力水平增长更快，最终预应力损失更小。

（5）锚索预应力在不同的地震波作用下，预应力损失并不相同。

[1]谷德振.岩体工程地质力学基础[M].北京：科学出版社，1979.

[2]戴自航，刘志伟，刘成禹，等.考虑张拉与剪切破坏的土坡稳定数值分析[J].岩石力学与工程学报，2008，27(2)：375-382.

[3]戴自航，卢才金.边坡失稳机制的力学解释[J].岩土工程学报，2006，28(10)：1191-1197.

[4]张倬元，王士天，王兰生.工程地质分析原理[M].北京：地质出版社，2005.

[5]赖杰，方玉树.考虑抗拉强度的含外倾结构面岩质边坡稳定性分析[J].后勤工程学院学报，2011，27(6)：7-12.

[6]郑颖人，叶海林，黄润秋，等.地震边坡稳定性分析探讨[C].中国力学学会2009学术大会论文集，2009.

[7]郑颖人，叶海林，黄润秋.地震边坡破坏机制及其破裂面的分析探讨[J].岩石力学与工程学报，2009，28(8)：1714-1723.

[8]Itasca Consulting Group，Inc..Fast Lagrangian analysis of continua in three dimensions(version 3.0)user′s manual[R].[S.l.]：Itasca Consulting Group,Inc.,2003.

[9]郑颖人，赵尚毅，孔位学，等.极限分析有限元法讲座I——岩土工程极限分析有限元法[J].岩土力学，2005，26(1)：163-168.

[10]郑颖人，赵尚毅，李安洪，等.有限元极限分析法及其在边坡中的运用[M].北京：人民交通出版社，2011.