自重作用下曲线连续刚构桥扭转效应初探
2012-06-13王超肖荣
王超,肖荣
(重庆市建筑科学研究院,重庆 400020)
0 引言
为了满足路线线路需求或功能要求,曲线梁桥的修建越来越多[1]。但是由于曲线梁桥存在弯扭耦合作用,使其较之直线桥梁的受力和变形更加复杂,使得设计施工以及后期的检测养护存在较大难度。本文以泥溪沟2号大桥为例,对其扭转变形进行研究,总结曲线连续刚构桥的扭转变形规律,以期为同类型的曲线连续刚构桥的施工监控提供参考。
1 工程概况
泥溪沟2号连续刚构大桥其孔跨布置为左线 (6×30+75.25+140+75.25+2×30)m、 右线 (6×30+75.25+140+75.25+3×30)m;主桥采用混凝土变截面预应力连续刚构箱梁,在桥跨方向上箱梁的跨中和根部梁高分别为3m、8.8m;顶板厚度(等厚度)为30cm,底板厚度从根部的100cm渐变到跨中的30cm,腹板厚度从根部至跨中分50cm、60cm、70cm三种厚度;箱梁顶板宽度为12.25m,其中翼缘悬臂长2.65m,底板宽度为6.95m;悬浇T构在纵向上被对称划分成16个节段;梁段数及梁段长从根部至跨中分别为8×3.5m、8×4.45m,边跨和中跨合拢长度均为1.8m。[2]该大桥平面位于曲线半径2000m的曲线上,其立面图和平面图如图1所示。
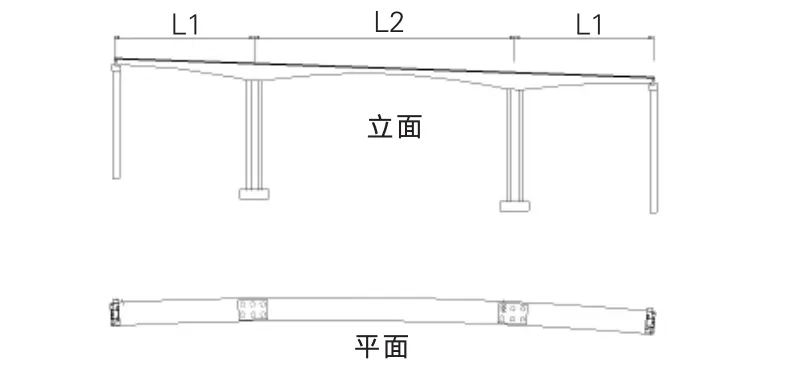
图1 大桥设计图
2 分析模型的建立
在保证截面及跨径布置不变的前提下,分别建立了曲线半径为200m、400m、800m、2500m的直线桥的有限元仿真模型,用以分析随着曲率半径的变化,对刚构桥扭转效应的影响。论文中所涉及的模型上部结构和下部结构共被划分成136个单元,其中88个单元为上部结构单元,48个单元为下部单元。当曲线半径一定时(以200m曲线半径为例),本文分析了墩高分别为60m、80m、120m三种情况时对结构的影响规律。采用Midas civil软件计算时,桥梁所涉及的材料参数均按《公路钢筋混凝土及预应力混凝土桥涵设计规范》JTGD62-2004[3]采用,材料的本构关系选取如图2所示。
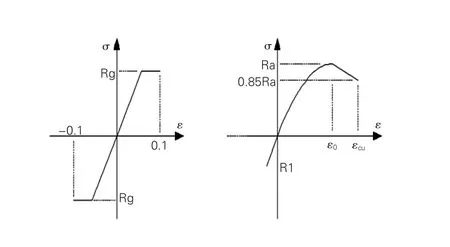
图2 钢筋及混凝土的应力-应变曲线图
(1)混凝土本构关系如下表达:
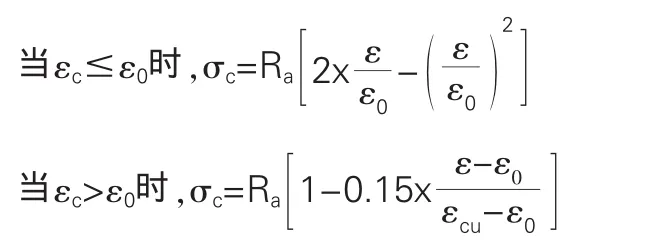
(2)钢筋本构关系如下表达:
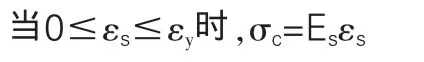
当εs>εy时,σs=Rg
式中:εc、εs、σc、σs为混凝土和钢筋的应变、 应力, Es、Eg为混凝土和钢筋的弹性模量,Ra为混凝土的标准强度,相当于σmax,ε0为相应于Ra时的混凝土压应变,εcu为混凝土的极限压应变。
3 连续刚构在自重作用下的计算结果及分析
无论在施工过程中还是成桥状态,自重较之二期恒载和可变荷载对施工监控中的线形控制起到决定性的作用,故该文着重研究自重对该桥型扭转效应的影响。借助对这一主要因素的研究,找出扭转变形的控制截面以及曲线半径与扭转角的关系。为了方便叙述将模型中的各参数的含义表述如下。
文中扭转角的含义为顶板翼缘板的内外两侧竖向位移的差值与梁宽的比值如图3所示,即:tgθ=Δh/B;正负号代表的意义为:向曲线内侧转为正,向曲线外侧转为负[4]。
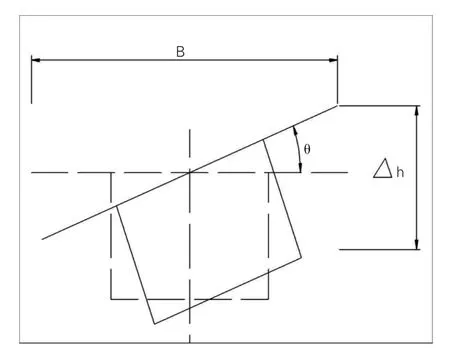
图3 扭转角示意图
1节点和89节点分别是桥梁主梁端点,24节点和66节点分别是左右两个桥墩的中心。
在自重作用下,曲线桥受弯扭效应影响,主梁不但产生竖向弯曲,而且在扭矩作用下产生主梁截面内的扭转变形。图4、图5分别显示了相同墩高、不同曲率及曲率相同、墩高不同时连续刚构桥的扭转角沿桥纵向的变化。

图4 曲线半径与扭转角关系图
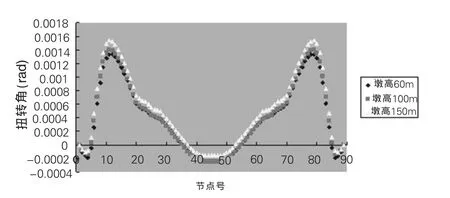
图5 桥墩高度与扭转角关系图
3.1 中跨变形结果分析
墩高一定时,沿桥跨方向上扭转角呈现一定的规律性。表现在梁体在扭矩作用下向曲线外侧扭转,同时中跨跨中附近主梁外边缘竖向位移要大于内边缘竖向位移,并且最大的扭转角发生在中跨跨中截面。曲线半径为200m的刚构桥与直线桥相比转角为0.02o,内外侧的高差为4.3mm,各曲线半径桥梁中跨跨中截面的变形计算结果见表1。在施工监控线形控制时,应特别注意这一影响。

表1 中跨跨中截面扭转角和内外高差
3.2 边跨变形结果分析
墩高一定时,从距中跨跨中2/7L2到距边跨端部1/8 L1截面处产生向曲线内侧的扭转。其中正扭转角在边跨跨中附近达到最大值。各曲线半径桥梁边跨跨中截面的变形计算结果见表2。值得提出,桥面越宽这一差值也越大,故当桥梁的宽度较大时应特别注意该截面扭转所造成的内外高差的影响。当曲线半径≥800m时,自重引起的边跨跨中截面的内外高差≤3mm,并且变化速度很慢,因为自重这一控制因素对扭转角影响甚微,而预应力在该截面处产生相反的扭转角[4],与自重扭转角部分抵消。可以断定当曲线半径大于800m时,可按直线桥进行施工控制;当曲线半径<800m时,应考虑曲率对桥面线形的影响,而且该种桥型的扭转角控制截面为中跨跨中截面和边跨跨中截面。
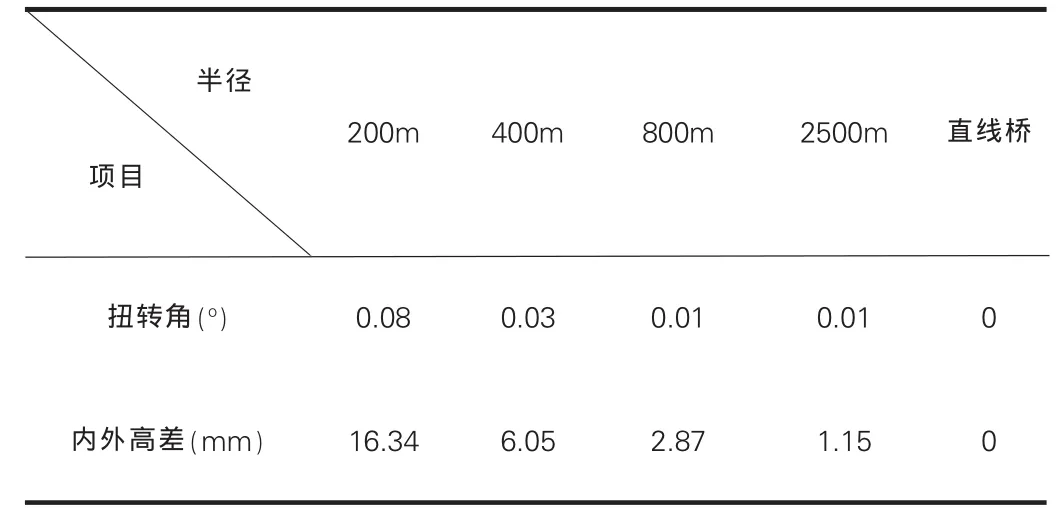
表2 边跨跨中截面扭转角和内外高差
3.3 墩高变化对变形结果影响分析
曲线半径不变,随着墩高的增加主梁中跨跨中的竖向位移逐渐增加。与此同时,该截面的扭转角增大即内外缘高差也增大。计算结果显示曲率半径为200m时,墩高分别为60m、100m、150m的连续刚构桥,中跨跨中截面内外侧的高差为2.1mm,详见表3计算结果,与直线桥相比较可以忽略不计。
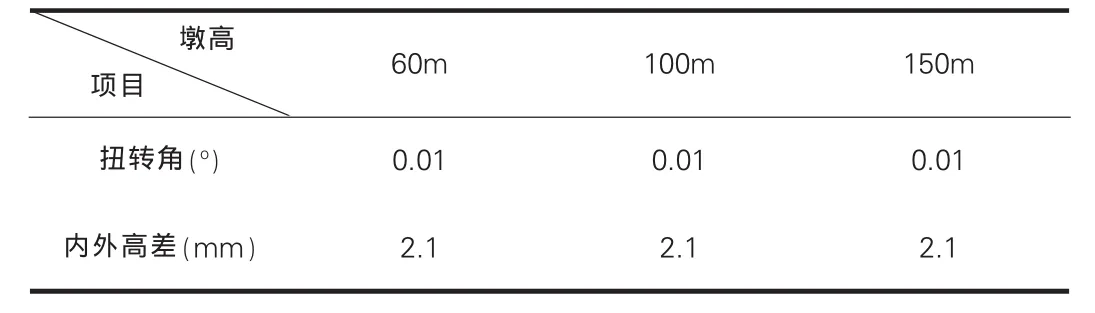
表3 曲线半径200m中跨跨中截面扭转角内外高差
4 结论
研究证明,该种桥型中跨跨中及边跨跨中截面的扭转角较大,故在泥溪沟2号大桥的线形控制中,将该两个截面作为了控制截面,着重对该截面的扭转角进行控制。大桥合拢后,实际测量证明,由于对控制截面的有效控制,桥面线形良好。
经分析,当曲线半径≥800m时,曲线连续刚构桥在自重和预应力的相互作用下扭转效应甚微,由于泥溪沟2号大桥的曲线半径超过800m,故在其施工监控中按直线桥进行了变形计算,依次作为监控的基础。
墩高的变化对连续刚构桥扭转效应的影响不是很显著。当曲线半径一定、墩高在0~150m变化时,各个截面扭转角基本一致,可以不考虑墩高变化对扭转的影响。
[1]李莉,舒赣平.小曲率半径曲线钢箱梁桥设计研究[J].建筑结构,2011,41(增刊1):244.
[2]孙广华.曲线梁桥计算[M].北京:人民交通出版社,1994:64.
[3]JTGD62-2004公路钢筋混凝土及预应力混凝土桥涵设计规范[S].北京:人民交通出版社,2004:10-13.
[4]王超.曲线连续刚构桥空间受力分析[D].重庆:重庆交通大学,2011:11-64.
