结合RS纠错编码和Walsh变换的软扩频技术

唐大宇

(中国西南电子技术研究所,成都 610036)

结合RS纠错编码和Walsh变换的软扩频技术

唐大宇

(中国西南电子技术研究所,成都 610036)

为了解决实际工程中信号被干扰的问题,增强纠检错能力,并提高保密性,提出了一种结合了RS纠错编码和Walsh变换的软扩频技术。通过对RS纠错编码产生和利用Walsh函数与复合码技术的Walsh变换方法的研究,以及和一般直扩频的比较,利用Matlab仿真阐述了软扩频技术的优势,并介绍了这种软扩频技术在实际工程中的应用。

软扩频;RS纠错编码;Walsh变换;复合码

1 引 言

扩频技术在现代数据通信中有着广泛的应用。扩频一般分为直接序列扩频和跳频两种,而软扩频是一种基于直接序列扩频、结合编码技术衍变而来的扩频技术,因为其具有的高保密性和强抗干扰能力[1],被越来越多地应用在信号处理等实际工程中。

一般的直扩系统的实现是将信息码与伪随机码进行模2加来获得扩展后的序列,但是,软扩频是不一样的,软扩频一般采用编码的方法来完成频谱的扩展,即用几位信息码元对应一条伪随机码。软扩频的实质是(N,k)编码,是用序列长度为N的伪随机序列与k比特的数据编码一一对应,是从信息空间向伪随机编码空间的映射,两个空间都是2k维的有限元空间,信息空间的元素与伪随机码空间的元素一一对应。与一般直扩系统不同,其扩频增益比较小,且不为整数,伪随机码空间的2k个长为N的伪随机码是正交的,因此,软扩频又可称为正交扩频。

软扩频因为结合了编码,所以软扩频的方法非常多,本文介绍一种结合了RS纠错编码[2]和Walsh变换[3]的软扩频技术。本文从 RS纠错编码和Walsh变换的基本原理出发,深入分析其变换过程,并使用一种采用复合码技术的改善Walsh变换,来提高这种软扩频技术的性能。

2 RS纠错编码

RS纠错编码是一类纠错能力很强的多进制BCH码,不但可以纠正随机错误、突发错误以及二者的组合,而且可以用来构造其他码类。在RS(n,k)码中,输入信号分为 k·m 比特一组,每组包括k个符号,每个符号由m比特组成。一个纠t个符号错误的 RS码有如下参数:码长(n符号或nm比特);信息段(k符号或km比特);监督段(n-k=2t符号或m(n-k)比特);最小码距(d=2t+1符号或m(2t+1)比特)。

域在RS编码中起着重要的作用,每个符号都可以看成是域中的一个元素,RS编码的运算都是定义在域中,域GF(2m)有 2m个符号,设 2m=q,GF(2m)=[0,α0,α1…αq-2],下面构建一个 m 为 4的伽罗华域;设m=4,本原多项式p(x)=x4+x+1,因为 α为p(x)的根,可以得到 α4+α+1=0,即α4=α+1,由此可得域中的元素如表1所示。

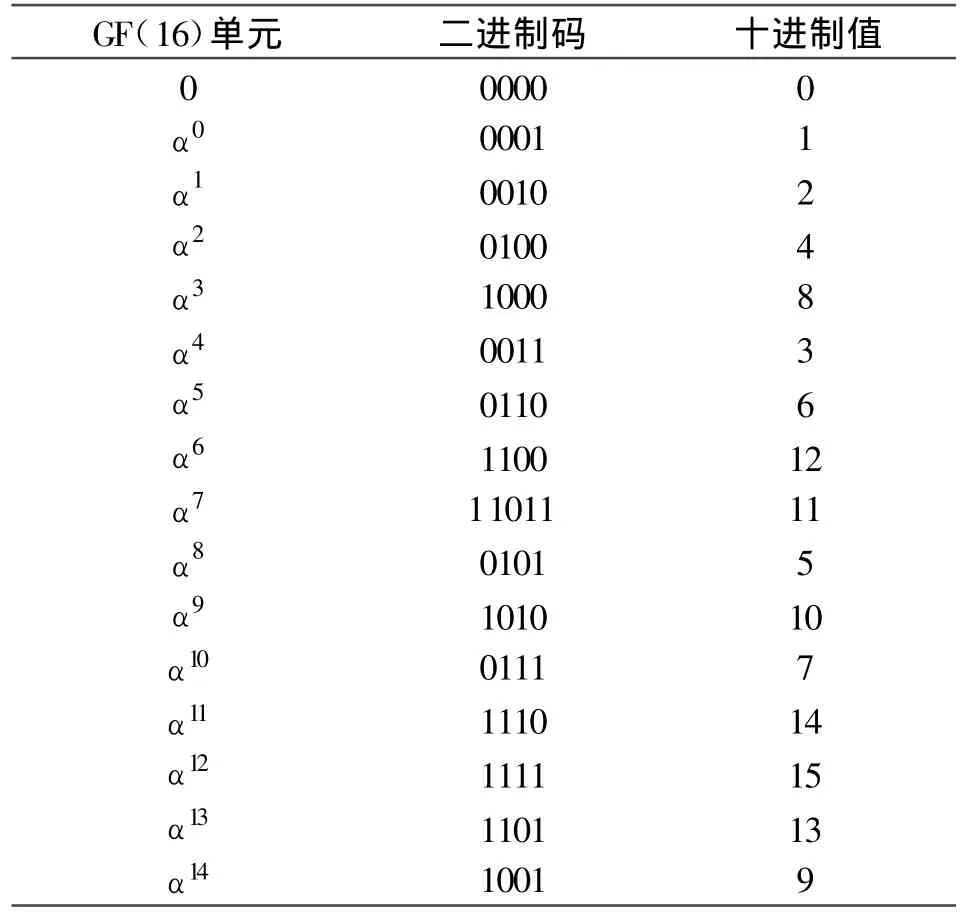
表1 伽罗华域Table 1 Galois Field

RS码的生成多项式为

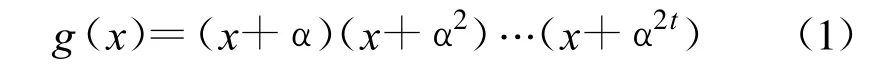
式中,αi为伽罗华域GF(2m)中的一个元素。假设一种RS(15,9)编码,即输入信号为 9位,每位4 bit,变换后为15位,纠错能力为3位,生成多项式为

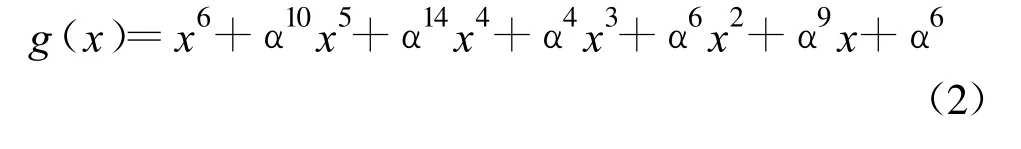
从二进制码的角度来看,这是一个(60,36)码,经过编码后生成6位RS纠错码,和9位的输入信号组合成一个15位的信号。编码采用公式:

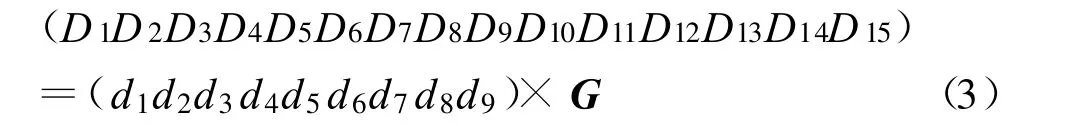
其中,G为生成矩阵,表示为

RS纠错编码由于采用了m进制,所以它是多进制调制时的自然和方便的编码手段。因为RS码能够纠正t个m位二进制码,所以适合在衰落信道使用,以克服突发性差错。

3 Walsh变换

式中,sgn为符号函数,对于sgn[x],当 x>0时,值为+1,而当 x<0时,值为-1;k、j取值0或1是由序数k的二进制码来决定,即:

3.1 普通的 Walsh变换

Walsh函数在通信中也称为Walsh码,它是美国数学家Walsh于1923年提出的一类完备的正交函数系,其最大的特点是每个函数仅取+1、-1两个值,比较适合用来表达和处理数字信息[4],因而在信号处理、图像处理、通信及计算机等众多领域得到了广泛的应用。

Walsh函数系一般可以分为3类,即Walsh序的Walsh函数系、Paley序的Walsh函数系和Hadamard序的Walsh函数系。这3类函数的区别在于它们各个函数出现的编号不同。这3种序的本质是一样的,它们之间可以通过变换矩阵相互转换。在此仅给出Walsh序的Walsh函数。所谓Walsh函数系是指下列函数系:

Walsh函数系的所有函数的周期都是1,并且函数的取值在单位区间[0,1)上均非零,因此称Walsh函数系为全局函数。由上述定义可以得出Walsh函数前16个Walsh函数的值:

如果把其中的1取为1,-1取为0,则可以得到如表2所示的一种按顺序排列的Walsh函数表。

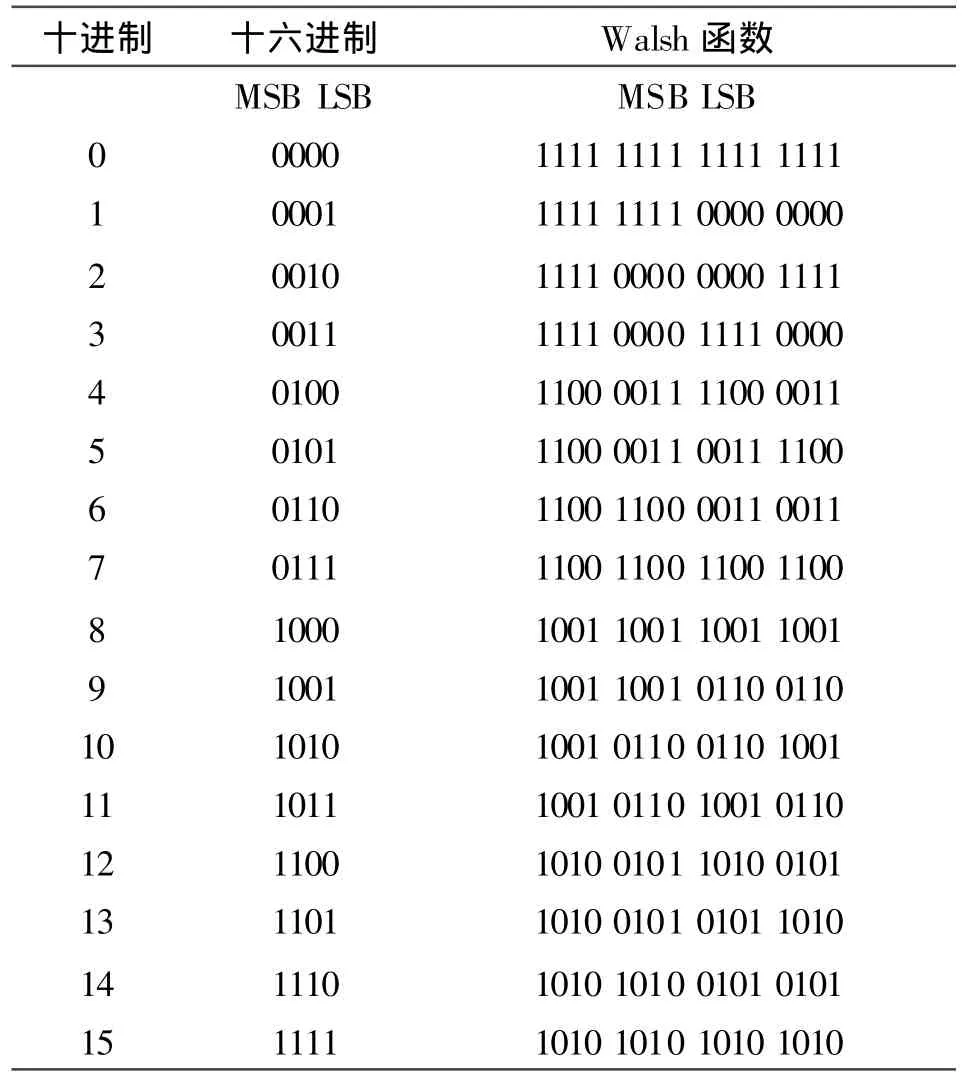
表2 Walsh函数Table 2 Walsh Functions

在Walsh变换时,将m个信息比特作为一个调制符号,选用一个M(=2m)个正交码中的一个进行变换,一个扩频序列传输m比特信息,提高了传输效率。当扩频增益相同时,Walsh码变换系统带宽只需传统直接序列扩频系统带宽的1/m,特别适合带宽有严格限制的环境。

通过Walsh变换,增加了信号的数据位长度,使得信号的抗噪性得到了提高,而且由于Walsh的相关性,使得变换后的信号具有一定的容错能力。通过一个仿真,可以了解Walsh变换的作用。仿真采用MSK调制方式,一个4 bit的数据在信噪比为8 dB时,不能正确解码,加入Walsh变换后,在有一定的错码存在的情况下可以通过相关来得到正确的原码。假设原码为1101,根据表2,得到变换后的码为1010010101011010。

首先建立一个无软扩频的模型,如图1所示,信噪比为8 dB。

图1 无软扩频模型Fig.1 No-soft-spectrum-spreading model

图2为无软扩频仿真结果,其中第一栏为原始数据,第二栏为调制后的信号,第三栏为解调后的数据。从图中可以看出,在信噪比为8 dB的情况下,调制后的数据已经较差,在解调后无法得到正确的原始数据。

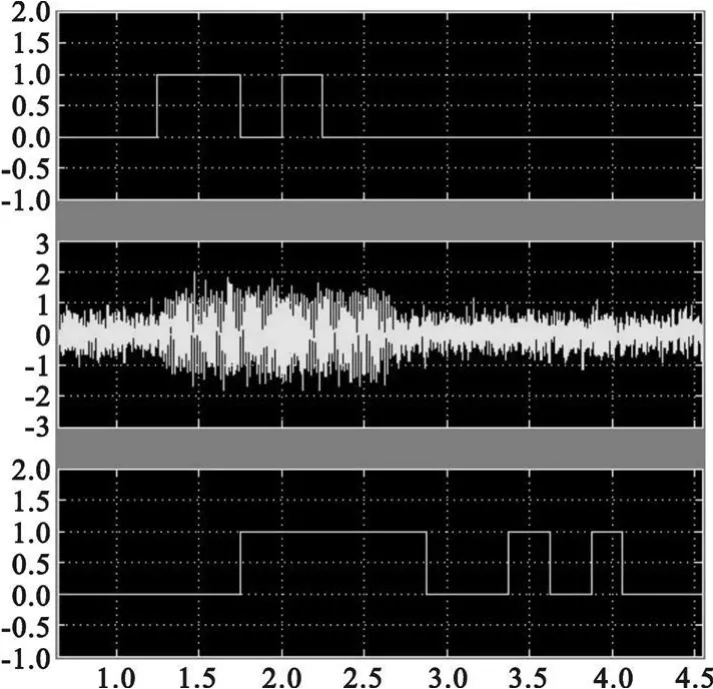
图2 无扩频的仿真结果Fig.2 Simulation result of no-soft-spectrum-spreading

再模拟工程应用来建立具有Walsh变换的仿真模型,信噪比依然为8 dB,16个相关器为Walsh中的16个扩频码,如图3所示。

图3 软扩频系统模型Fig.3 Soft spectrum spreading system model

图4为软扩频仿真结果,其中第一栏为扩频后的数据,第二栏为扩频后数据的调制信号,第三栏为解调后的扩频数据。可以看出,解出来的码依然是有错误的,但这时还没有进行相关处理。

图4 软扩频数据的仿真结果Fig.4 Simulation result of soft spectrum spreading

将得到的解调数据与16个相关器进行相关和积分处理后,可以得到该数据与伪随机码101001010101 1010的相关性最高,但其中含有两个错码,误码率为12.5%。图5显示了两位错码的位置(其中第一栏为解调数据,第二栏为原始数据,两根竖线标注的位置为错码位)。再通过反查Walsh表得到1010 0101 0101 1010对应的数为1101,与原始数据是完全相同的。

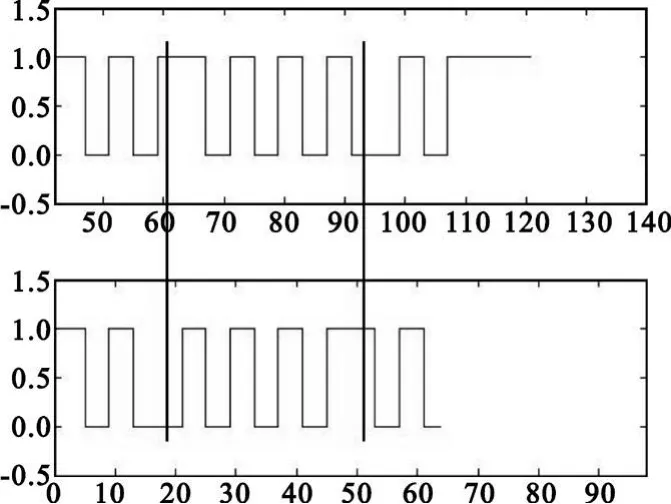
图5 错码位Fig.5 Faulty code bit

通过仿真可以看出,加入Walsh变换后信号的抗噪性明显增加了,根据公式

可以得出Walsh变换的扩频增益为H dB。有了这H dB的增益后,信号的灵敏度可以得到很大的提高。

3.2 改善的 Walsh变换

由于信号的传输是非同步传输,在这种情况下Walsh码的自相关函数和互相关函数均不理想,具有较大的旁瓣;而且,Walsh码各码序列的功率谱分布彼此不均匀相同,不能独立承担扩频任务。这时需要构造一个相关特性较好的伪随机码(通常为m序列)来和Walsh码进行复合(模2加),得到复合码。复合码既保持了Walsh码的同步正交性,又大大改善了其相关函数的特性,减少了旁瓣,具有良好的非同步相关性。

伪随机码的相关性对扩频系统性能的影响非常大。要使系统性能保持稳定,选择的伪随机码互相关性应该较好,因为m序列的周期性自相关函数最为理想,所以选择m序列做为伪随机序列。m序列伪随机序列的发生器由N级移位寄存器作为主支路,用若干级模2加加法器和各级移位寄存器抽头组成线性反馈支路。输出的序列并非真正的随机序列,而是一个周期为2N-1位的重复序列,其中 N表示生成这个序列的移位寄存器的长度。

在相同噪声和相同扩频增益的情况下,对使用了复合码的Walsh变换和直接扩频的误码比特率进行仿真,结果如图6所示,可以看出在信号衰减较小时使用了复合码的Walsh变换系统和直接扩频系统的误码率相差不大,但在信号衰减较大时,使用了复合码的Walsh变换系统比直接扩频系统有更低的误码率。

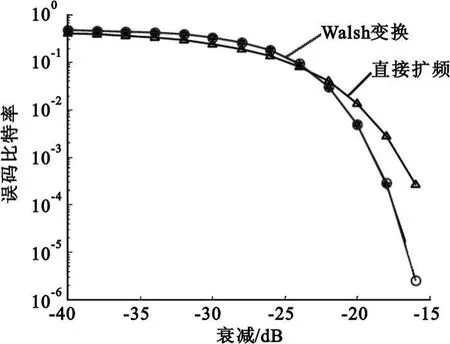
图6 误码比特率比较Fig.6 BER comparison

4 工程应用

在实际工程中,信号存在着各种干扰,而且在现代战争中,信号的保密性也是非常重要的。这种结合了RS纠错编码和Walsh变换的软扩频技术在实际工程中有着非常强的适用性。

在工程中信号首先经过RS纠错编码和Walsh变换,再进行MSK调制后送给信道发射;接收时先进行MSK解调,再进行Walsh反变换和RS纠检错并解码,最终得到原信号。系统框图如图7所示。

图7 系统框图Fig.7 Block diagram of the system

在经过RS纠错编码后,信号的保密性得到了提高,根据RS的特性,可以在解码时对一定的错码进行检测和纠正。而Walsh变换更是提高了信号的抗干扰能力,使得信号更加可靠,这在实际工程中是非常有用的。

与普通的软扩频技术相比,这种方法不仅具有一般扩频的保密性和抗干扰能力,而且有一定的纠错能力。

5 结束语

本文通过对RS纠错编码和复合Walsh变换产生方法的研究,深入分析了两种方法在工程应用中的优势,并和普通的直接扩频进行了比较,发现信号通过RS纠错编码后增加了数据位的长度并可以对信号进行纠检错,而Walsh变换将每一位的比特长度进行了扩展,并通过与伪随机码复合后得到复合码,信号在传输过程中经常被各种噪声干扰,信号之间也存在着叠加,将这两种技术结合而成的软扩频在正交性和纠错方面都有良好的表现,对信号处理和分析有着很大的帮助,在实际工程中有很强的应用性。软扩频技术是近年来比较新的一种扩频技术,其中可以延伸和扩展的地方很多,相信通过对编码方法的研究,可以得到更好的软扩频方法。

[1]曾孝平,王宇峰,刘劲.软扩频技术及其编码与性能分析[J].重庆邮电学院学报,2001,22(4):22-25.

ZENG Xiao-ping,W ANG Yu-feng,LIU Jing.Principle of Tamed Spread Spectrum System and the Coding and Performance Analysis[J].Journal of Chongqing University of Posts andTelecommunications,2001,22(4):22-25.(in Chinese)

[2]刘剑锋,霍效新.一种基于RS码序列的软扩频系统及其Simulink仿真[J].信息与电子工程,2007,5(6):441-443.

LIU Jian-feng,HUO Xiao-xin.A Novel Tamed Spread Spectrum System Based on RS Code and Its Simulation by Simulink[J].Information and Electronic Engineering,2007,5(6):441-443.(in Chinese)

[3]童莹,张健.基于GPU的快速二维沃尔什变换研究[J].微电子学与计算机,2011,28(1):46-49.

TONG Ying,ZHANG Jian.Research of Fast 2-D Walsh Transformation Based on GPU[J].Microel Ectronics&Computer,2011,28(1):46-49.(in Chinese)

[4]李斯伟,陈惠萍.基于宽带信号的Walsh码扩频通信[J].通信技术,2000,109(4):75-79.

LI Si-wei,CHEN Hui-ping.Walsh Code SS CommunicationBased on Broadband Signal[J].Communications Technology,2000,109(4):75-79.(in Chinese)

TANG Da-yu was born in Chengdu,Sichuan Province,in 1978.He received the B.S.degree in 2001.He is now an engineer.His research concerns the digital signal processing for the secondary radar systems.

Email:iceshadowcn@163.com

Soft Spectrum Spreading Technique Combining RS Error-correction Coding and Walsh Transforming

TANGDa-yu
(Southwest China Institute of Electronic Technology,Chengdu 610036,China)

In order to solve signal interference in practical engineering and improve error-correction as well as encryption capability,a soft spectrum spreading technique combining RS error-correction coding and Walsh transform is proposed.Through RS error-correction codes generation,Walsh transform method research with help of Walsh function and composite coding,and comparison with conventional direct spectrum spreading,advantage of soft spectrum spreading technique is discussed based on Matlab simulation.Furthermore,practical engineering is also introduced.

soft spectrum spreading;RS error-correction coding;Walsh transform;complex code

TN914.4

A

10.3969/j.issn.1001-893x.2012.06.022

1001-893X(2012)06-0943-05

2012-02-20;

2012-05-15

唐大宇(1978—),男,四川成都人,2001年获学士学位,现为工程师,主要研究方向为二次雷达数字信号处理。