基于压缩传感的图像过完备字典设计

赵 睿，于华楠

(1.东北电力大学信息工程学院，吉林吉林132012;2.东北电力大学信息工程学院，吉林吉林132012)

传统的信号采集过程主要包括采样、压缩、传输和解压缩四个部分。在运用百万像素的数码相机对场景进行成像时，对图像信号的压缩是在不影响成像效果的前提下，舍弃了采样获得的大部分数据，只对部分信息进行存储和传输，最后在接收端通过相应的解压缩算法对原始图像进行重构［1］。Donoho于2006年正式提出了压缩传感的概念，其优点在于信号的投影测量数据量远远小于传统采样方法所获得的数据量，突破了奈奎斯特采样定理的瓶颈［2］。并且，压缩传感技术能够通过观测直接获得压缩的信号，避免对海量像素信息的采集，并同时实现去噪过程［3］。

压缩传感技术在图像采集、图像压缩和医学成像等领域具有广阔的应用前景，文献［4］中给出了压缩传感技术及其在图像处理方面应用的详细综述，文献［5］将空间自适应滤波技术应用到压缩传感理论中，提出了一种新的图像重建算法。本文对压缩传感中的过完备字典设计方法进行研究，将K-SVD算法［6］与MP，BP和FOCUSS等稀疏编码算法结合使用，利用K-SVD算法更新字典。仿真实验结果表明，本文设计的过完备字典能够更好的补偿图像丢失的像素，具有明显优于DCT过完备字典的图像去噪能力。

1 压缩传感理论

压缩传感的核心思想是将压缩与采样合并进行，首先采集信号的线性非自适应投影值，即测量值，然后根据相应重构算法由测量值重构原始信号。假设x是一个N维向量，满足其中:D是过完备字典，且u∈RN中只有K个非零元素，即u是N维维稀疏向量。

将信号x分解成一个矩阵D和一个稀疏向量u的乘积在信号处理过程中具有重要的意义，x可以用u中的K个非零元素来描述，而不再是原来x中的N个元素。同样，为了在噪声环境中估计x，我们只需要估计出K个而不是N个实际参量。

压缩传感可以从相对少的样本中恢复稀疏信号，而不需要复杂的计算过程。对x的采样过程可以描述为一个线性变换，即通过观测矩阵Φ得到观测信号

其中Φ是M×N维观测矩阵，观测到的信号y有M个元素，y的每个元素是x的一个检测量。将式(1)代入式(2)得

若已知D和Φ，利用重建算法就能从y中恢复出x，而不必知道未知信号u中非零元素的一系列位置。

2 过完备字典的设计方法

过完备字典的设计通常基于信号分解理论。传统的信号分解变换是将信号分解在一组完备的正交基上，而且这种变换是可逆的，如傅立叶变换、小波变换等。

本文对过完备字典D的设计基于下述假设:不考虑图像的采集过程，于是不需要对图像信号进行再次观测，即观测矩阵为单位矩阵。过完备字典的设计可以看成是求解下式所描述的问题

过完备字典的自适应设计方法一般由两个阶段组成，第一阶段根据当前的字典计算稀疏表示系数，这一阶段称为稀疏编码;第二阶段在稀疏表示系数固定的条件下更新字典。这两个阶段不断交替进行，直到训练出符合要求的过完备字典。

2.1 字典设计第一阶段

在给定的训练信号y和当前字典D的条件下，计算出稀疏表示系数u，这一稀疏编码过程和压缩传感理论中的稀疏重建过程是一致的。所以计算稀疏表示系数需要解决下式描述的问题

稀疏编码阶段认为D是固定的，如果选择单位l2范数来约束D，则式(4)中的约束条件可以写成

这样，式(4)描述的问题可以转化为若干个独立的子问题，这些子问题可以利用上述跟踪算法来解决。

2.2 字典设计第二阶段

在自适应方法的第二个阶段，本文采用K-SVD算法［6］更新字典。K-SVD算法采用奇异值分解(SVD)方法更新过完备字典，每次更新一个列向量dk，而其它的列向量都保持不变，以便找出新的dk和与之对应的系数，从而最大限度的减少均方误差。在字典更新阶段，D和X都是固定的。假设只处理D中的列向量dk和与之对应的系数xiT(X的第i行，不是X的第i列向量xi)，则更新字典时式(6)中给出的约束条件可以表示为

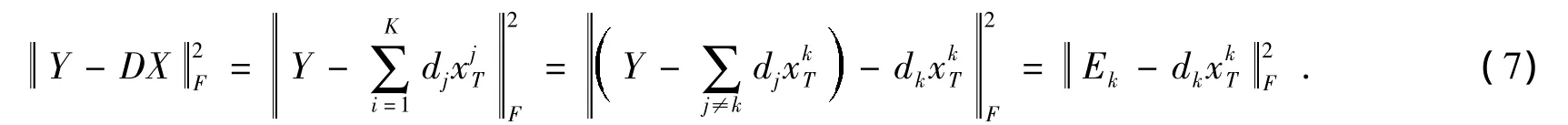
式中，把矩阵的乘积DX分解成K个秩为1的矩阵之和，其中第k个是要处理的，其余K-1个保持固定不变，矩阵Ek代表除去第k个原子的所有N个训练信号的误差。

3 仿真实验

为了验证过完备字典在图像去噪中的应用及本文训练的字典和DCT过完备字典的实际效果，本文进行下面几组仿真实验。实验中使用测试图像lena，原始图像和噪声污染后的图像如图1所示。人为加入的噪声污染基于以下方法:将图像分割成500个不重叠的块，取常数r∈(0.2，0.9)，然后随机删除每个块中r倍像素总数的位置(置0)。图2给出了图像去噪过程中采用的字典，字典的各个子块是按照方差递减的顺序排列的。前三个子图是采用本文的自适应方法训练得到的字典，其中第一个是利用原始图像训练得到的字典，第二个和第三个字典是在噪声污染图像的基础上训练得到的字典，字典1和字典2被噪声污染的程度不同。第四个子图是DCT过完备字典。在字典的训练过程中，稀疏编码计算选择匹配跟踪算法，误差容限选择0.000 4。

图1 测试用图像

图2 图像去噪使用的字典

针对受噪声污染的图像，分别采用两种字典去噪后的实验结果如图3所示。从实验结果可以看出，信噪比为31 dB的情况下，基于本文提出的方法训练得到的字典，具有更强的去噪能力，能够实现更优的图像重建效果。而进一步对比采用自适应方法训练的两种字典，由于图像噪声的存在，细节信息被干扰，利用原始图像训练得到的字典重建的图像更清晰，但是原始图像通常是未知的，所以只能利用受噪声污染的图像进行训练。

图3 两种字典的图像去噪效果

为了对比两种训练字典的方法，分别采用上述两种方法获得的过完备字典进行图像重建，得到的平均重建误差曲线如图4所示。从图中可以看出，随着被腐蚀像素在总像素中所占的比例上升，自适应训练字典和DCT字典的平均重建误差都不断增加，但自适应方法的平均重建误差始终低于DCT字典的平均重建误差，当被腐蚀像素在总像素中所占比例达到0.9(90%)以上时，两种字典的去噪效果都受到被腐蚀像素的严重影响，平均重建误差趋于一致。

图4 两种字典的平均重建误差曲线

4 结 论

本文对图像压缩传感中过完备字典的自适应训练方法进行研究。采用K-SVD算法更新字典，在更新字典中列向量的同时更新系数，加快了收敛速度。仿真实验证明了本文采用的自适应算法训练的字典在图像去噪方面明显优于DCT字典，具有较低的平均重建误差。此外，使用信噪比越高的，即越接近原始图像的图像来训练字典，图像去噪的效果越明显。在进一步的研究中，将尝试实验更多的稀疏编码算法，并且对算法进行改进以适用于处理较大的图像。

［1］杨晓慧，焦李成.基于第二代bandelets的图像去噪［J］.电子学报，2006，34(11):2063-2067.

［2］D.L.Donoho.Compressed Sensing［J］.IEEE Transactions on Information Theory，2006，52(4):1289 - 1306.

［3］D.L.Donoho.De-noising by Soft Thresholding［J］.IEEE Trans on Information Theory，1995，41(3):613 - 627.

［4］J.Haupt and R.Nowak.Compressive Sampling Vs Conventional Imaging［C］.2006 IEEE International Conference on Image Processing，2006:1269-1272.

［5］Karen Egiazarian，Alessandro Foi，and Vladimir Katkovnik.Compressive Sensing Image Reconstruction via Recursive Spatially Adaptive Filtering［C］.IEEE Conference on Image Processing，2007:549 -552.

［6］M.Aharon，M.Elad，and A.M.Bruckstein.The K-SVD:An Algorithm for Designing of Overcomplete Dictionaries for Sparse Representations［J］.IEEE Transaction Image Process，2006，54(11):4311 - 4322.