无线传感器网络极小连通支配集算法的改进*

张 静，贾春福，杨 挺

(1.天津工业大学工程教学实习训练中心，天津300387;2.南开大学信息技术科学学院，天津300071;3.天津大学电气与自动化工程学院，天津300072)

集成了传感器、微机电系统和网络三大技术而形成的传感器网络是一种全新的信息获取和处理技术［1－3］。在无线传感器网络中，除了少数节点需要移动以外，大部分节点都是静止的。它要求设计的算法必须具有快速收敛的特性，减少路由查找的开销，提高路由发现的性能和效率。基于最小连通支配集的路由方法是一个很好的分层路由［4－7］方法，它将路由过程简化到生成的较小的子网中。这意味着在先应式路由中只有网关节点需要维持路由信息，而在反应式路由中研究空间被简化到这个MCDS中。MCDS中的网关节点构成了高一级的虚拟骨干网，而每个网关节点在自己的簇中都起着控制中心的作用，用于路由分组和广播路由信息。明显地，这种方法的有效性很大程度上依赖于发现和维持一个MCDS及与之相应的子网的大小。不幸的是，对大部分图来说，求一个MCDS的问题属NP－C问题［8］，在实际应用中需要设计近似求解算法。目前已有的算法主要分两类，集中式算法［9－10］和分布式算法［11－17］。集中式算法要求每个节点具有整个网络的拓扑结构信息，因而不适合移动网络多变的特点，可伸缩性差。分布式算法的主要思想是通过节点之间的局部交互操作在网络中迅速构造一个虚拟骨干网。

有关连通支配集的算法，国内外已经有许多人从事这一方向的研究。其中WL［11，17］提出了求解连通支配集的简单且有效的方法，随后又提出多种改进算法［12－16］。WL算法求解连通支配集分为标记阶段和优化阶段，由于分步实施算法具有不完整性，即缺乏措施将两个连续的阶段衔接起来，所以使单个节点无法判断下一个阶段何时开始，因此具有不完整性。本文首先提出连通支配集的数学模型，基于WL算法进行优化改进，提出IWL算法并通过仿真说明算法的有效性。

1 算法

1.1 定义

用一个连通的简单无向图G=(V，E)来表示无线自组传感器网络，其中:V是一组节点的集合，每个节点表示一个传感器;E是一组边的集合，每条边e=(u，v)∈E(其中 u，v∈V)表示节点 u 和节点 v彼此都在对方的无线发射范围内。节点u的相邻节点集记为N(u)。节点u的相邻节点闭集记为N［u］。

定义1 一个图G的某个节点子集D是支配集(DS)是指G中所有在V－D中的节点都至少和D中的一个节点相邻。图G的支配集D称为连通支配集(CDS)是指由 D诱导的子图 G［D］是连通图。CDS中的节点称为支配节点，也称为网关节点;不在该集中的节点则被称为非支配节点或非网关节点。如果图G中没有比D更小的连通支配集，则D称为最小连通支配集(MCDS)。

1.2 数学模型

我们先描述出该图的支配集的数学模型，然后选出部分节点作为支配节点，保证支配集连通，得到的就是连通支配集的数学模型。

对于支配集需要满足:任何V－D节点至少要与一个集合D内节点相连。用以下数学模型描述支配集:

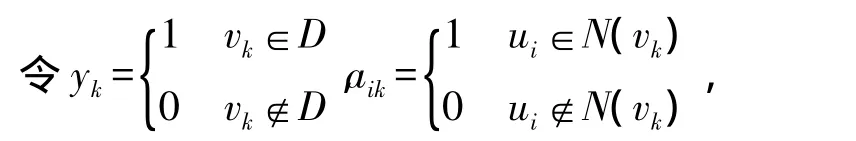
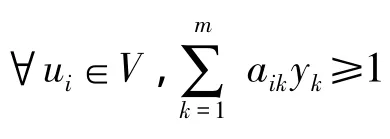
对于支配集内支配点有两种可能不连通。如图1(a)和1(b)所示。

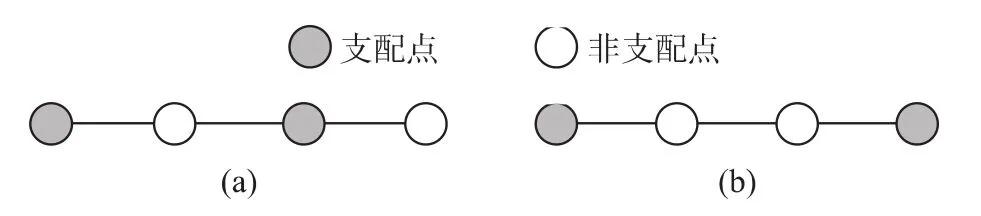
图1 支配集不连通示例

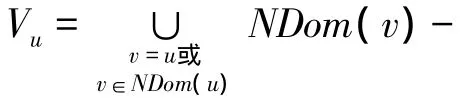
综上所述，极小连通支配集的数学模型表示如下:

目标:

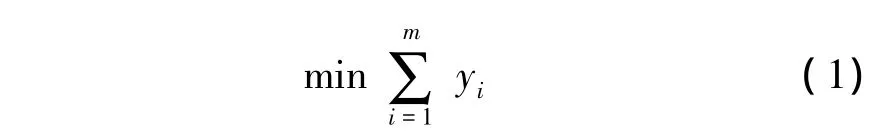
约束:

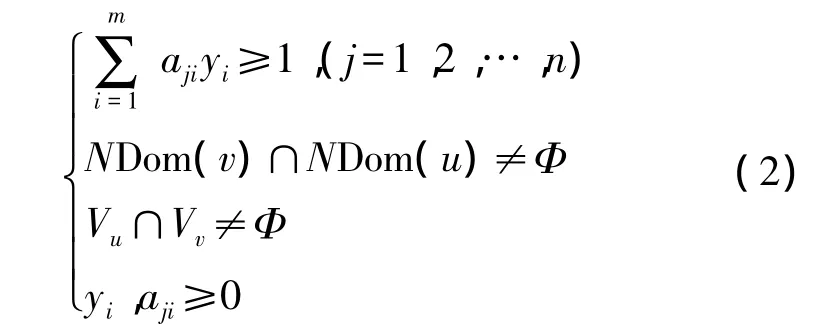
1.3 WL［11］算法回顾

标记过程:给定一个连通的简单无向图 G=(V，E)，M(v)标记节点v是否为支配点，M(v)=T为支配点，F为非支配点。假定初始时每个节点都是非支配点，N(v)={v|{v，u}∈E}表示节点v的邻节点开集合。

(1)初始每个节点M(v)=F;

(2)每个节点v向它的邻居节点广播它所有的邻节点开集合N(v);

(3)当节点接收到所有邻节点的信息后，如果存在两个不相邻的节点，则宣布自己为支配点，即M(v)=T。

上述标记过程求出连通支配集，接下来通过优化规则减少CDS的大小。在网络中，给每个节点分配唯一标识的 id，N［v］是节点 v的邻节点闭集合，N［v］=v∪N(v)。

Rule 1:在支配集内两个相邻节点u和v，如果N［v］⊆N［u］，并且 id(v)＜id(u)，则将 v标记为非支配点。

当N［v］=N［u］时，节点v或u都可以标记为非支配点，为了保证仅有一个节点变为非支配点，选择节点id较小的那个节点标记为非支配点。

Rule 2:假定在支配集内节点v和w与节点u相邻，如果 N(v)⊆N(u)∪N(w)，并且 id(v)=min{id(v)，id(u)，id(w)}，则将 v标记为非支配点。

1.4 IWL 算法描述

在WL算法的标记过程中，只有当节点v的所有邻居节点都是相互连通的，也就是导出的子图是完全连通图时，节点v才会标记为非支配点。在无线传感器网络中，节点被随机抛撒在一定区域，大部分节点都会有两个邻居节点是不相邻的，只有极少数节点的所有邻居节点是相互连通。所以WL算法的标记过程只能使得极小部分节点变为非支配点，主要是通过优化规则再精简连通支配集的大小。但是我们可以看到，在 Rule 1，如果节点 v和 u满足 N［v］⊆N［u］，但是 id(v)＞id(u)，那么节点 v不会被标记为非支配点。同样在Rule 2中，如果节点u，v，w 满足 N(v)⊆N(u)∪N(w)，但是 id(v)不是最小的话，节点v也不会被标记为非支配点。在WL算法中节点id的引入主要是避免当N［v］=N［u］时，节点u，v同时变为非支配点。

基于上述分析，我们可以对上述WL算法进行改进，提出IWL算法。该算法中标记过程可以省略，直接对图G应用改进的优化规则，一次完成而不需分阶段执行，这样就消除了由于分步实施算法具有的不完整性。初始时标记网络中所有节点都为支配点，算法描述如下:

Rule 1a:假定u，v都是支配点，节点v满足下列任意条件可以标记为非支配点:

Rule 2a:假定支配点u和w是支配点v的邻居节点，节点v满足下列任意条件可以标记为非支配点:

算法的执行步骤如下:

(1)假设初始所有节点为支配节点，所有节点首先发送hello消息给周围邻居节点，收集到邻居节点信息后形成N(v)，并将N(v)广播给邻居节点。

(2)接收到邻居节点发送的N(v)消息后，开始运行Rule 1a，如果满足Rule 1a则变为非支配点，否则保持支配点不变。并将节点的最新状态信息广播给周围邻居节点。

(3)当节点接收到所有邻居节点发送的最新状态信息后，开始运行Rule 2a，如果满足Rule 2a则变为非支配点，否则保持支配点不变。

(4)算法结束。

定理1 运行IWL算法后形成的支配点集是该网络的连通支配集。

证明:算法假定初始所有节点都是支配点，Rule 1a是指当支配点v所支配的节点也同时被支配点u支配的话，那么节点v可以变为非支配点，这样可以使得节点v周围的所有节点还能被节点u所支配，同时与节点v相连的支配点可以与支配点u连通。Rule 2a是指当且仅当支配点v的所有邻居节点能被支配点u或w同时支配的话，那么节点v可以变为非支配点，这样可以使得节点v周围的所有的非支配节点还能被支配，同时与节点v相连的支配点可以与支配点u或w相连，因此运行完该算法之后剩余的支配点集是该网络的连通支配集。

定理2 IWL分簇算法中，整个网络的广播消息量复杂度为O(n)。

证明:算法初始所有节点发送信息，消息量为n;任意节点v将N(v)广播给邻居节点，消息量为n;节点宣布为非支配点发送消息m个，其中m为非支配点的个数。IWL分簇算法整个广播消息量为(2n+m)，所以，整个网络的广播消息量复杂度为O(n)。

定理3 IWL分簇算法中，整个网络的时间复杂度为 O(Δ2+nlgΔ)。

证明:IWL分簇算法中，网络的时间复杂度就是单个节点最坏情况下的时间复杂度之和，每一个节点都要与周围邻居节点比较，Δ为节点的最大度，单个节点比较花费O(lgΔ)。所有节点同时运行规则Rule 1a，花费O(Δ2)，剩余支配点运行规则Rule 2a，算法最坏情况是所有节点运行规则Rule 1a后都保持支配点，n个节点运行规则 Rule 2a，所以给出IWL分簇算法整个网络的时间复杂度为 O(Δ2+nlgΔ)。

1.5 IWL算法图例说明

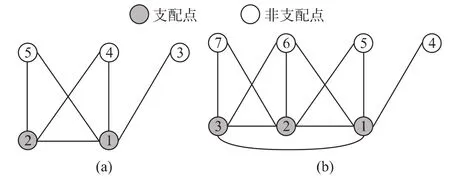
图2 算法中Rule 1a和Rule 2a的图示说明

为了说明算法有效性，通过图例说明IWL算法的执行过程。给定图2(a)所示，初始时节点都是支配点。N(1)={2，3，4，5}，N(2)={1，4，5}，N(3)={1}，N(4)={1，2}，N(5)={1，2}.N［2］⊂N［1］，N［3］⊂N［1］，N［4］⊂N［1］，N［5］⊂N［1］，通过Rule 1a(2)，节点2，3，4，5 都变为非支配点。

为了说明IWL算法较WL算法的优越性，我们也通过图例进行说明分析。给定图2(a)所示支配集，不难看出N［2］⊆N［1］，但是 id(2)＞id(1)，则不满足 WL的优化规则Rule 1，所以节点2不能标记为非支配点。由于N［2］⊂N［1］，N［1］⊄N［2］，满足本文给定的Rule 1a(2)，因此节点2可以标记为非支配点。同样给定图2(b)，N(2)⊆N(1)∪N(3)，但是 id(2)＞id(1)，则不满足WL的优化规则Rule 2，所以节点2不能标记为非支配点。由于N(2)⊆N(1)∪N(3)，N(3)⊆N(1)∪N(2)，但是 N(1)⊄N(2)∪N(3)，id(2)＜id(3)，满足本文给定的Rule2a(2)，因此节点2可以标记为非支配点。

类似于参考文献［14－17］中提出的改进算法，上述规则中节点id可以替换为节点的度数或节点能量级别。当规则中选择节点度数大的作为支配点，则可以减少支配集的大小;如果选择能量级别高的节点作为支配点，能够有效延长每个节点的平均寿命。

2 仿真及结果分析

为了评价算法IWL，我们以实例进行计算机仿真，并与 WL［11］算法和 WMCDS［16］进行比较，评估算法在生成较小连通支配集的性能。

测试所用的拓扑通过如下方法产生:在长度L=100 m，宽度W=100 m的区域内随机播撒数目为N的节点，假定每个传感器节点都有相同的通讯半径R，这样产生的图为简单无向图。然后设定节点的通讯半径R，如果两个节点的距离小于R，在这两个节点间将有一条连线。通过下面的步骤计算连通支配集:

(1)首先判断产生的该随机图是否连通。如果不是连通图则重新进行播撒，否则进行下一步。

(2)对随机图分别应用IWL算法、WMCDS算法和WL算法，计算产生的支配集所占的比例。

设计了两类实验:一类是通讯半径R固定为40 m时，不断按步长5个增加节点数从30个到80个;另一类是节点数目固定为40个，不断按步长为5 m增加通讯半径由30 m到80 m。对每一个节点/通讯半径的组合，随机生成50个拓扑，对于每个拓扑进行实验，运行本算法。我们得到图3和图4的模拟结果。分析实验曲线可以发现，随着拓扑节点数(或者单个节点发射距离)的增加，三个算法产生的连通支配集所占的比例都在减少，而IWL算法优于其他两个算法。在节点间连通性较强的情况下，IWL算法和WMCDS算法以及WL算法均可以得到很好的结果。因此IWL算法性能整体上是优于其他两个算法的。

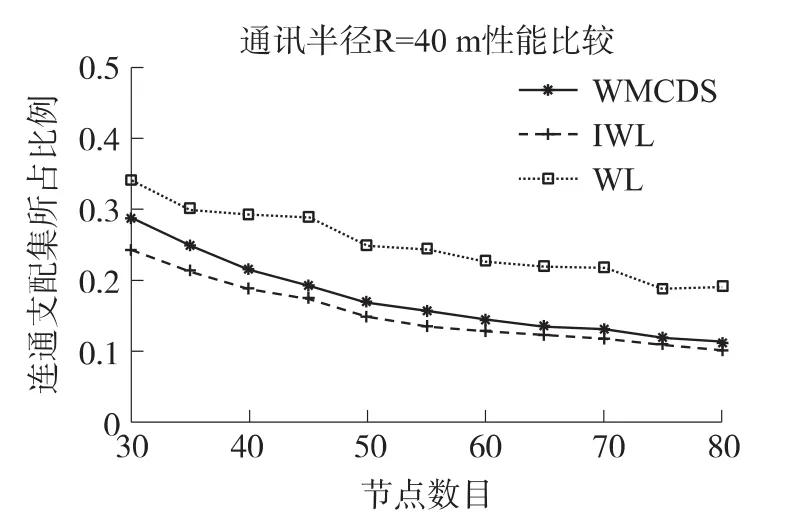
图3 通讯半径固定性能比较

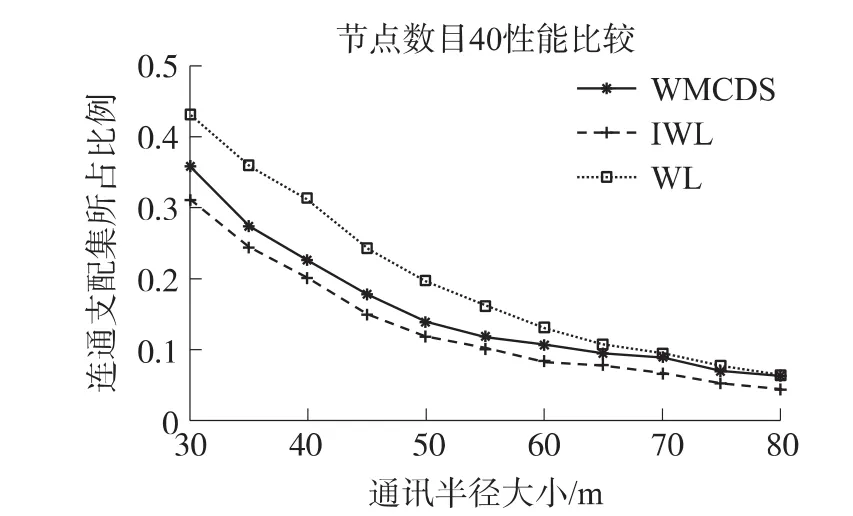
图4 节点数目固定性能比较

3 结论

本文根据WL算法，提出的一种简单有效的分布式算法IWL，解决了WL算法分步实施的缺点，使得求解连通支配集的算法得到简化。算法只要求网络节点具有局部的网络拓扑信息，克服了集中式算法需要搜集整个网络拓扑信息的缺点，因而算法的可伸缩性好。仿真结果表明，算法能有效地得到较小的网络连通支配集，其性能优于被比较的分布式算法。此算法可以在网络中自动形成一个虚拟骨干网，从而可为网络中的广播和路由操作提供一个有效的通信基础。

［1］ 任丰原，黄海宁，林闯.无线传感器网络［J］.软件学报，2003，14(7):1282－1291.

［2］ 孙雨耕，张静.无线自组传感器网络［J］.传感技术学报，2004，17(2):331－335，348.

［3］ 马祖长，孙怡宁，梅涛.无线传感器网络综述［J］.通信学报，2004，25(4):114－122.

［4］ Yi S，Heo J，Cho Y，et al.PEACH:Power-Efficient and Adaptive Clustering Hierarchy Protocol for Wireless Sensor Networks［J］.Computer Communications，2007(30):2842－2852.

［5］ 杨伟，刘润杰，申金媛.一种基于LEACH的高效节能协议［J］.传感技术学报，2010，23:1153－1157.

［6］ Stanislava S，Henizelman W B.Cluster Head Election Techniques for Coverage Preservation in Wireless Sensor Networks［J］.Ad Hoc Networks，2009，5(7):955－972.

［7］ Muhammad Tariq，Yong Pyo Kim，Jun Hwan Kim，et al.Energy Efficient and Reliable Routing Scheme for Wireless Sensor Networks［C］//2009 International Conference on Communication Software and Networks，2009:181－185.

［8］ Garey M L，Johnson D S.Computers and Intractability;A Guide to the Theory of NP-Comleteness［M］.San Francisico;W H Freeman，1979.

［9］ Chiang C，Wu H，Liu W，et al.Routing in Clustered Multihop Mobilewireless Networks with Fading Channel［C］//IEEE Singapore International Conference on Networks，1997，Singapore，1997:197－211.

［10］ Ravi Prakash.A Routing Algorithm for Wireless Ad Hoc Networks with Unidirectional Links［J］.Wireless Networks，2001，7:617－625.

［11］ Wu Jie，Li Hai-Lan.On Calculating Connected Dominating Set for Efficient Routing in Ad-Hoc Wireless Network［C］//Proc Third International Workshop on Discrete Algorithms and Methods for MobileComputing and Communications(DIAL M’99)，Seattle，1999

［12］彭伟，卢锡成.一个新的分布式最小连通支配集近似算法［J］.计算机学报，2001，24(3):254－258.

［13］张静，孙雨耕，房朝晖.能量有效的最小连通支配集近似算法［J］.传感技术学报，2004，17(4):603－606，610.

［14］阎新芳，孙雨耕，胡华东.基于极大权的最小连通支配集启发式算法［J］.电子学报，2004，32(11):1774－1777.

［15］张静，贾春福.基于自适应拓扑变化的无线传感器网络路由协议［J］.天津大学学报，2007，40(9):1054－1059.

［16］ Zhang Jing，Jia Chun-Fu.Minimum Connected Dominating Set Algorithm with Weight in Wireless Sensor Networks［C］//The 4th International Conference on Wireless Communications，Networking and Mobile Computing.2008.1－4.

［17］ Wu Jie，Gao Ming.Stojmenovic on Calculating Power-Aware Connected Dominating Sets for Efficient Routing in Ad Hoc Wireless Networks［C］//Proceedings of the IEEE International Conference on Parallel.Valencia:IEEE Computer Society Publisher，2001.346－353.