一种新的保险投资组合优化模型

2012-06-11张月曲坤王丽媛

大连交通大学学报 2012年1期

张月，曲坤，王丽媛

(1.大连理工大学应用数学系，辽宁大连116024;2.大连交通大学理学院，辽宁大连 116028)

0 引言

在保险市场中，保险公司通常把所有的风险项目看做一个整体，根据不同的风险项目在整个投资组合中所占的比例对被保险人收取合理的保费，根据收取保费的大小以达到安全运营的目的.然而在保险和金融市场中，风险无处不在，保费的制定自然离不开对风险的合理度量，风险表示损失的不确定性及其发生的概率.目前关于风险度量的方法有很多种，如:方差原理［1］、破产概率［1］、VAR 方法［2］、一致性风险度量方法［3］等.不同的度量方法取决于对风险的不同认识，结果往往也不同.常见的方差原理［1］中，方差依赖于随机变量取值的大小，它表示收益的各种可能值与期望收益的偏离程度，因此只能计算出关于损失变量的二阶矩，并且方差作为不确定性的度量只适用于损失分布是正态分布(即对称分布)的情况，对于其他的偏斜分布(尖峰、厚尾等)，方差无法正确反映出风险的大小，因此在实际应用中这种度量方法存在着不足.而熵代表不确定性程度的度量，它根据随机变量可能取到的概率进行计算，不依赖于随机变量本身取值的大小，它表示的是概率密度偏离均匀分布的程度，是把风险系统看做一个整体进行度量.在保险研究中，人们最关心的是极端事件发生时风险的大小，即文献［1］中所讲的破产概率，这时损失的概率分布是非对称的，仅用方差来度量的风险大小显然不够，还应包括损失的高阶矩信息，而熵代表高阶矩，因此可以用熵作为方差度量风险的一个有效补偿.文献［1］通过将破产概率中的安全系数转化为方差，用方差度量风险.基于以上对方差和熵的对比分析，本文用熵来作为方差度量保险投资组合中风险的补充，提出一种度量风险的新模型:均值－方差－熵模型，以便使风险的度量更加有效.

1 预备知识

在信息论中，熵代表无知程度的度量，它的值越大，意味着我们对所解决的问题知道的信息越少.金融和保险市场的信息是不完全的，也就是存在一定的不确定性即风险，随着不确定性的减小也就是熵的减小，我们才能更加有效地将风险控制住，本文基于熵作为风险的度量，以文献［1］中的聚合风险模型为基本假设，将保险投资组合中各风险项目所占的比例(即损失变量的概率分布)转变成对风险项目所收取的保费的表达式，得到了关于保费的优化模型，在给出具体的优化模型之前，我们先来介绍一下该模型的理论依据:

1.1 最大熵原理及其数学表达［4］

所谓的最大熵原理就是在根据部分信息进行推理时，我们应使用的概率分布，必须是在服从所有已知观测数据的前提下使熵函数取最大值的那个概率分布.熵最大，表明我们除了具有统计矩的信息外，对待求的概率分布一无所知.这是我们能做出的仅有的无偏分配，因此最大熵原理可表达为下述数学规划问题:

其中，p=(p1，p2，…，pn)为待估的概率分布，gj(j=1，2，…，m)表示各阶统计矩函数，E(·)是由实验观测得到的各阶统计矩的期望值.

1.2 聚合风险模型基本假设［1］

2 均值－方差－熵优化模型

保险业的存在是由于人们愿意支付高于他们的期望索赔额的保费以寻求保险保障，而保险公司的收益等于他们收取的保费减去其索赔额(其中不考虑其他运营成本).因此如何定价一个合理的保费才是保险公司决定一个有效的保险投资组合的关键.

假设保险市场有k个不同的风险项目ψ1，ψ2，…，ψk，每个风险项目 ψj包含 Nj种不同风险索赔Sj，其中Sj服从泊松参数为λj的复合泊松分布.对于ψj中的任一风险，保费为xj=λjE［X］+lj，其中xj代表保费;lj代表风险负载.

假设风险项目ψj在保险投资组合中所占的比例为nj，其大小取决于所收取的保费 xj，且，因此保险投资组合的收益为:

为保费 x=(x1，x2，…，xk)的函数.

式(2)的矩母函数为［1］

则累积矩母函数为

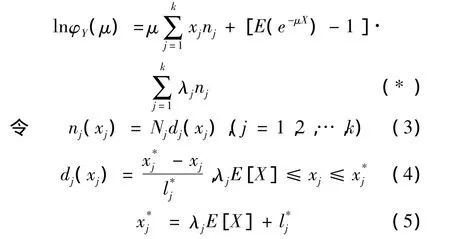
因此均值－方差－熵优化模型为:

由式(*)可得保险投资组合的期望收益和方差分别为累积矩母函数的一、二阶矩在μ=0处的值，即

由于E［X2］的大小与优化问题并没有太大的关系，因此为方便起见令E［X2］=1.

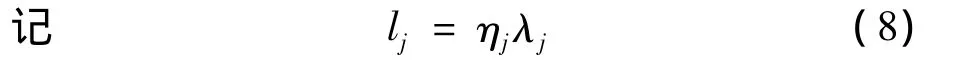
ηj代表风险厌恶指数.

将(4)，(5)，(7)代入(3)得

将式(9)，(10)，(11)代入上面优化模型整理得:

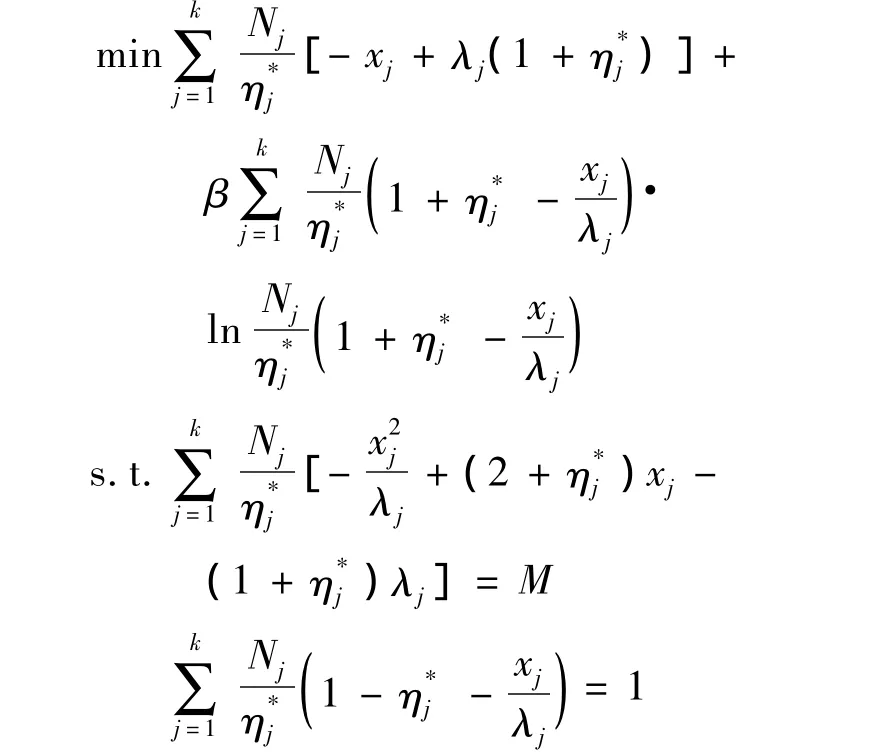
可见该模型将投资比例nj转化为了关于保费xj的表达式，它不同于一般的均值－方差优化模型，其约束条件是关于保费xj的二次函数，其中包含一次项并且不包含混合项，通过调节加权系数β的大小可以求解该凸规划问题.该问题为凸规划问题，一定有唯一最优解，即我们可以计算出保费xj.当β很小时，求得的保费xj结果主要是方差起作用而熵函数不起作用，而随着β的增加，熵函数起的作用逐渐增加，这样求得的保费xj主要是熵函数在起作用.