无人机在运动舰船上着舰视觉导引技术研究
2012-06-10王广彪李华伟丁文锐李红光
王广彪,李华伟,丁文锐,李红光
(1.北京航空航天大学,北京 100191;2.中国电子科技集团第54 研究所,石家庄 050081)
0 引 言
舰载无人机的高性能、低成本和能在恶劣条件下执行任务等特点,使得舰载无人机的发展成为一种趋势。然而在航母的整个作战链条中,舰载无人机的降落是事故率最高的环节。这主要是因为海上恶劣的作战环境导致的,所以研究一种能在恶劣环境下正常工作的辅助导航着舰系统迫在眉睫。现有的导航方法有:全球定位系统(GPS)[1]、惯性导航系统(INS)[2]、视觉导航系统[3]及各种方式组成的组合导航系统[4]。其中GPS 受国外限制,当被关闭或干扰时,着舰系统的安全性和可靠性受到很大影响;惯性导航存在误差随时间无限增加的问题。相比之下,视觉导航技术是利用传感器获得图像,通过图像处理得到无人机导航定位姿态参数,视觉传感器具有轻便、低功耗和体积小等优点;此外,视觉导航系统的工作波段远离当前电磁对抗的频率范围,具有精度适中,成本低等优点,采用它独立完成或辅助完成无人机的自主着陆、着舰任务已成为国际上的一种发展趋势[5]。然而,以往的研究中均没考虑舰船在海面上做六自由度的运动对视觉导航算法的可靠性和精度的影响[6、7],还有海上可见度低等恶劣环境使得着舰过程变得更为危险。在这种背景下,提出了一种适用于海上恶劣环境下的无人机视觉导航着舰方法。
1 概 述
舰载无人机视觉着舰存在两个问题:一是海上可见度低;二是舰船在海面上做六自由度的运动,对视觉导航算法的可靠性和精度产生了很大影响。针对第一个问题,根据大气窗口及透射率特点,结合目标检测相关知识,设计了一个由五个分立的、有一定布置特点的红外圆组成的合作目标,根据理论知识并考虑一定的余度,设计了合作目标的位置、大小。针对第二个问题,分析了舰船运动简化模型,并根据简化模型提出了基于卡尔曼滤波提高导航精度的新方法。为验证上述两种解决方案的可行性,设计了一套基于上述两种解决方案的机舰相对位姿解算验证系统,总体框架图如图1 所示。
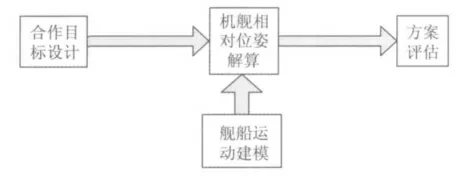
图1 总体框架图
框架主要分为四部分:合作目标设计、舰船运动建模、机舰相对位姿解算和方案评估。涉及四大关键技术:合作目标设计、合作目标识别定位、舰船运动建模和卡尔曼滤波进行精度补偿。
2 关键技术
2.1 合作目标设计
合作目标的设计包括合作目标辐射波段选取、合作目标形状设计、尺寸设计和目标位置布置。如图2 所示。
2.1.1 合作目标辐射波段

图2 合作目标设计
为适应全天候的舰载无人机着舰的需求,根据文献[7]中研究,选用红外辐射作为合作目标辐射的对应波段,波段选取8 ~12 μm 波段。辐射功率设计要求5 km 可以探测合作目标。在8 ~12 μm波段,设计合作目标2 kW,5 km 处探测接受功率为0.5 W,满足红外相机探测要求[8]。故设计合作目标辐射功率2 kW。
2.1.2 目标形状设计
圆形目标因其具有的各向同性特性,在处理轮廓模糊的红外图像中具有无可比拟的优势,同时用重心表征一个点的位置,增加了算法的鲁棒性和精度。同时,采用N 点算法作为解算机舰相对位姿的方法,根据文献[9]的分析,为保证实时性需求,选用四个点进行解算。但为了保证合作目标快速可靠的识别,采用五个独立的圆形作为合作目标并以特定方式布置在舰船上。解算过程中仅用边缘的四点进行解算,中间点作为辅助识别定位点。分布图如图3 所示。

图3 合作目标布置图
2.1.3 合作目标尺寸设计
根据文献[10]研究,为了实现机舰距离1 km时合作目标的可靠识别,并增加尺度余度,设计圆直径为5 m。
2.1.4 合作目标位置布置
如图3 所示:P3布置在第一根拦阻索和第二根拦阻索中间位置,且在航母横摇中心轴上。P2、P4与P3共线且平行于拦阻索。P1、P5在P2、P4、P3三点形成的线段的中垂线上。
设目标的探测距离为S(km),合作目标最小间距为D(m),为满足图像合作目标能够分辨开,根据瑞利判据,合作目标最小间距D 满足

式中,φ 为红外探测仪最小分辨角,φ =8.79 ×10-3度,当探测距离为1 km 时,D =1.11 ~1.67 m。选取D=15 m,满足分辨条件。即P2、P4、P5、P1相距P3分别为15 m、15 m、25 m 和35 m。
2.2 合作目标识别定位
合作目标识别定位分为两步:一是根据红外图像获得图像中各合作目标的像点位置;二是根据像点位置进行物像点匹配。
2.2.1 解算合作目标像点位置
针对海上环境背景单一,提出了一种快速的目标检测识别算法,如图4 所示。
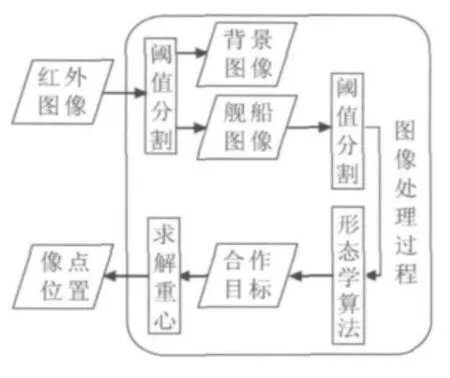
图4 合作目标识别定位
首先,对获得的图像进行第一次阈值分割,分离出舰船目标和背景图像;然后对舰船目标进行第二次阈值分割,并采用腐蚀、膨胀形态学方法分离出合作目标;最后求解每个红外圆的重心,用来表征红外圆的位置。本算法计算量小,解算实时性好,合作目标检测可靠性高。
2.2.2 物像点匹配
所谓物像点匹配,就是把图像中的点和舰船上的合作目标进行一一匹配。合作目标之间的距离比例关系具有仿射变换不变特性,适用于检测经平移、缩放、旋转后的合作目标。具体算法如下。
(1)选定在同一直线上的三个点,确定中间点为P3;
(2)分别计算两端点到中间点的距离,并进行比较;
(3)若距离相等,则证明此两点为P2、P4;若为此情况,选择另外在同一直线上的三个点进行步骤2;
(4)若不等,则距离大的为P5,小的为P1,从P1向P5看去,左边的为P2,右边的为P4。
经过上述判断即可确定物像点的对应关系。
2.3 N 点算法解算机舰相对位姿
N 点算法最先由德国数学家Grunert 进行了详细阐述[11],随后用于图像测量学[12]和计算机视觉等领域。用N 点算法解算飞机位姿的具体过程在文献[9、13]中,本文不再赘述。
2.4 舰船运动建模
航空母舰在海浪中由于受到风浪等因素的影响,会产生各种不规则的运动。若把航母视为一个刚体,当它在海面上航行时可产生六个自由度的运动,如图5 所示。其中以横摇、升降和纵摇对航母的影响最为显著[14]。

图5 航母在海上的六自由度运动
根据文献[15]中的研究,对这三个方向上的运动进行简化建模,如图6 所示,图6 中实直线表示航母质心所在的且平行于航母上表面的平面。
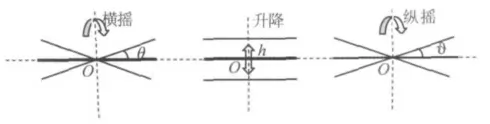
图6 舰船运动简化模型
简化模型下,舰船在平衡位置作微幅的简谐摇荡运动,航母的横摇角θ、升降高度h 和纵摇角ϑ 满足式(2)
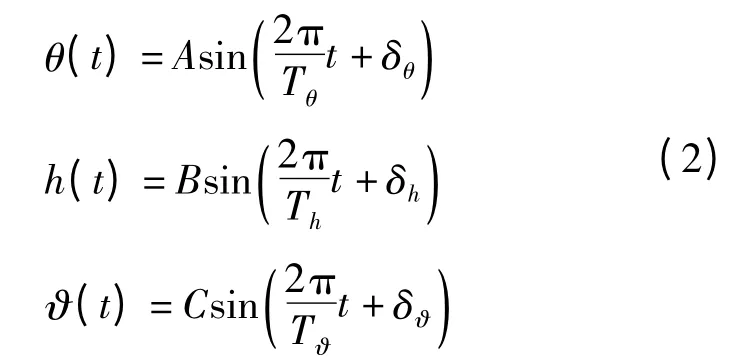
式中,A、B、C 为横摇角、升降幅度和纵摇角度的最大值;Tθ、Th、Tϑ为横摇、升降和纵摇周期;δθ、δh、δϑ为随机相位。
对上述两式离散化采样,得
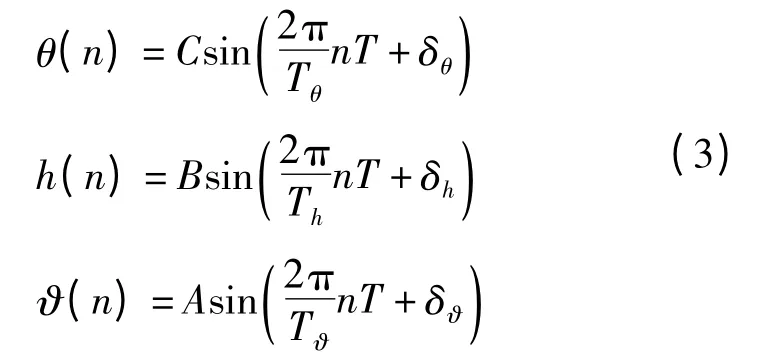
则其数学期望值[16]为
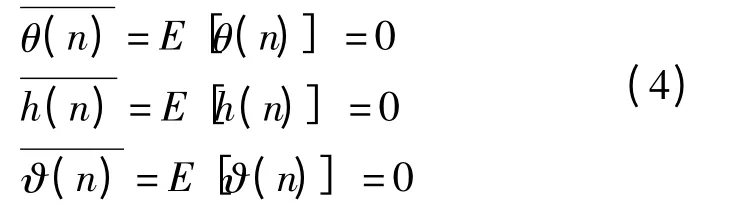
由式(4)可知横摇、升降和纵摇三个方向上的运动的随机抽样的均值为零,如图5 中的粗直线状态即为均值状态。这为下文提到的采用无人机飞行参数进行精度补偿提供了理论根据。
2.5 卡尔曼滤波进行精度补偿
海上环境恶劣,加之舰船的运动,使得导引精度误差很大,提高精度是非常有必要的。根据上文提出的简化模型,本文提出了一种利用卡尔曼滤波提高精度的方法。产生精度误差原因分为两部分,一是在图像处理时间Δt 内产生的相对位姿量;二是因舰船横摇、升降和纵摇造成的位姿偏差量。第一部分采用实时运算延时时间内飞机位移量来补偿;第二部分采用卡尔曼算法,具体运算表达式如式(5)。

式中,Pi为由第i 次图像处理得出的机舰相对位姿;Pi′为经过卡尔曼滤波后的相对位姿;qi为经过延时补偿后的舰船相对飞机的位姿(补偿在图像处理时间Δt 内产生的相对位姿量);(vx,vy,vz)T为飞机相对舰船的速度矢量;Δt 一般较小,位移与速度近似成线性;Δ SΔT(i-1)·i为在从采集第i-1 帧到采集第i帧的时间间隔内机舰相对位移矢量变化量;ΔT 为相邻两帧采集图像的时间间隔。
3 实验及结果
3.1 方案设定
实验采用5 个合作目标作为特征点进行解算机舰相对位姿。无人机从距离航母1 km 处以-4°的下滑角着舰,速度为70 m/s,航母以12 m/s 速度向正北方向行驶[17]。法国“克里蒙梭”号航母为保证舰载机在5 ~6 级海况下进行作业的适航标准为:横摇最大角度为3°,纵摇最大角度为1.4°,垂直位移最大为2.2 m[18]。选取升降最大幅度为1 m,周期为5 s;最大纵摇角度为0.5°周期为5 s;最大横摇角为2°,周期为5 s。图像采集帧率为10 Hz。实验中机舰位姿解算方案设计如图7 所示。

图7 机舰相对位姿解算
其中,图像处理过程具体流程如图4 所示,延迟时间包括图像处理、物像点匹配和数据处理所用时间;帧间时间为0.1 s。
经图像处理之后,可以得到合作目标重心在图像坐标系中的位置。然后根据位置关系判定图像中的各点对应的真实合作目标点。然后用N 点算法进行解算机舰相对位姿。
3.2 仿真实验
在Vega Prime 4.1 中进行仿真验证,实验设计的基于合作目标导航的无人机着舰视觉导引系统如图8 所示。机舰相距不同距离时无人机上摄像头拍摄的视景图像如图9 所示。经阈值分割后的图像如图10 所示。经过腐蚀、膨胀形态学算法处理后的合作目标图像如图11 所示。合作目标的重心分布图(图中白点位置)如图12 所示。




3.3 结果及分析
基于上述仿真条件,采用偏差量作为衡量方案可行性的标准。仿真结果与真实位姿的偏差量如图13 所示。
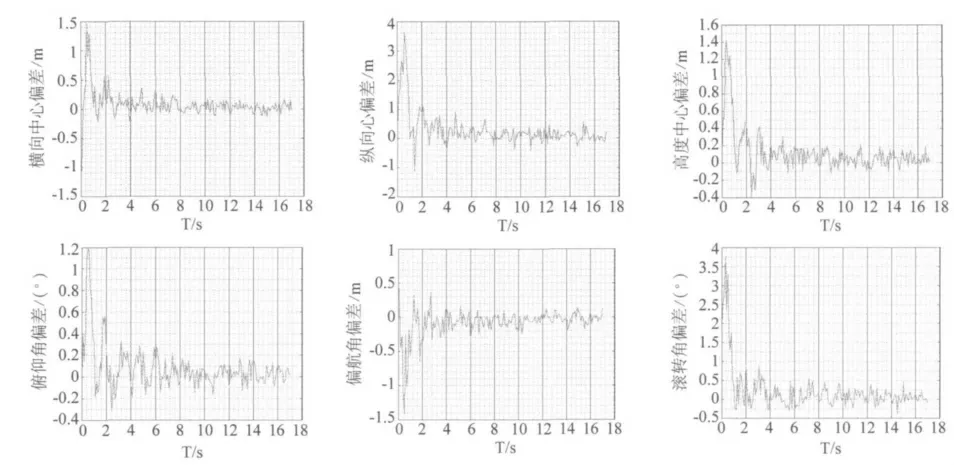
图13 位姿偏差量
由图13 可知,横向、纵向和高度三个方向位置偏差量均能在2 s 内降低至1 m 以内;滚转角偏差在3.6 s 内降低至0.5°以内;偏航角偏差在2 s 内降低至0.5°以内,并在4 s 后基本保证在0.2°以内;俯仰角偏差在1 s 以内降至0.5°以内,并在6 s 以后降低至0.2°以内;而且随着机舰相对距离的减小,六自由度方向上的偏差量逐渐减小,精度能够很快逼向精确值。实验结果表明本文所涉及方案能够满足无人机着舰要求。
4 结 语
视觉导航系统越来越广泛应用于独立完成或辅助完成无人机的自主着陆、着舰任务中。分析了低可见度和舰船运动对视觉引导方法的影响,并提出了解决方案,最后在Vega Prime 中对该方案进行了仿真验证,结果表明提出的无人机着舰视觉引导方法适用于低可见度、运动舰船上的无人机着舰。
[1]王惠南. GPS 导航原理及应用[M]. 北京:科学出版社,2003.
[2]秦永元. 惯性导航[M].北京:科学出版社,2005.
[3]CORY S S,SHAKERNIA O,SHANKAR S.A Vision System for Landing an Unmanned Aerial Vehicle[C]//Proceedings of 2001 IEEE,International Conference of Robotics and Automation,2001:21-26.
[4]艾伦,金玲,黄晓瑞. GPS/INS 组合导航技术的综述与展望[J]. 数字通信世界,2011(02):60-63.
[5]嵇盛育. 基于计算机视觉的无人机自主着舰导引技术研究[D]. 南京:南京航空航天大学,2008.
[6]SINOPOLI B,MICHELI M,DONATO G,et al.Vision Based Navigation for an Unmanned Air Vehicle[C]//IEEE Conference on Robotics and Automation,2001:1757-1765.
[7]嵇盛育,等. 基于红外视觉的无人机自主着舰合作目标的研究[J].红外技术,2007,29(10):593-597.
[8]张建奇,方小平. 红外物理[M]. 西安:西安电子科技大学出版社,2004 .
[9]李飞,等. 无人机视觉辅助着陆中的姿态和位置估算[J].电光与控制,2012,19(1):69-73.
[10]倪立学,等. 一种地面合作目标的研究与设计[J]. 光电工程,2007,34(7):8-13.
[11]GRUNERT J A.Das Pothenotische Problem in Erweiterter Gestalt Nebst Bber Seine Anwendungen in Der Geodäsie[J]. Grunerts Archiv für Mathematik und Physik,Band 1,1841:238-248.
[12]CHURCH E. Theory of Photogrammetry[M]. NY:Syracuse University Press,Bulletin 19,1948.
[13]QUAN LONG,LAN ZHONGDAN.Linear N-Point Camera Pose Determination [J]. IEEE Transactions On Pattern Analysis And Machine Intelligence,1999,21(8):774-780.
[14]李辉青,韩维. 航母横摇对舰载机着舰的影响研究[C]//湖南省第二届研究生创新论坛——航空宇航与控制科学分论坛论文集,2009,1(11):175-179.
[15]刘应中,缪国平. 船舶在波浪上的运动理论[M]. 上海:上海交通大学出版社,1986.
[16]周荫清.随机过程理论[M].北京:电子工业出版社,2006.
[17]许东松,刘星宇,王立新.航母运动对舰载飞机着舰安全性的影响[J].北京航空航天大学学报,2011,37(3):289-294.
[18]高奇峰.舰载机起降指导系统仿真研究[D]. 哈尔滨:哈尔滨工程大学,2006.
