基于SATAⅡ协议的CRC32并行算法的研究

朱佳齐，尹 蕾，许 晏，陈泉根

（中国工程物理研究院 电子工程研究所，四川 绵阳 621900）

随着通信和存储技术的发展，数据传输速率在急剧提高。然而由于通道传输特性不理想及可能受到干扰或噪声的影响，数据传输过程中难免会发生错误。如何保证可靠性是正确设计一个通信系统或数据存储系统的关键问题所在。

信道编码是提高可靠性的必要手段，实现检错功能的差错控制方法很多，包括奇偶校验、重复码校验、校验和检测、行列冗余码校验、恒比码校验、CRC校验等。其中CRC循环冗余校验是一种高效率的差错控制方案，其特点是编码和解码的方法简单、检错纠错能力强，因而应用于许多领域尤其是串行通信中以实现差错控制。

CRC循环校验算法占用的系统资源少，其实现方法分为软件实现和硬件实现。文中在研究CRC32算法的基础上，结合SATAⅡ协议的具体要求，实现了基于FPGA的CRC32并行算法。

1 CRC校验原理

CRC校验算法是利用线性编码理论，发送方根据一定的规则，生成要传送的n位信息码的r位校验码（CRC码），并将校验码附在信息码后面，最后发送（n+r）位二进制系列。而接收方利用信息码和校验码之间所遵循的同样规则对接受到的二进制系列进行校验，以判断传送中是否出错[1]。为了便于描述，n位信息码用多项式k（x）表示：

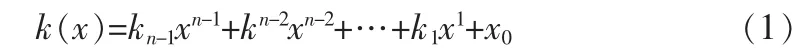
式中ki的系数取0或1。同样，用G（x）表示r+1位生成多项式，先在式（1）两端同时乘以 xr，则：

xrk（x）模 2 除以 G（x），得到的余数多项式为 R（x），商多项式为 Q（x），则：

由于求CRC校验码采用模2加减运算法则，即不带进位和借位的按位加减，这种加减运算实际上就是逻辑上的异或运算，加法和减法在逻辑上是等价的。在模2多项式代数运算中定义的规则有[2]:

由式（3）、式（4）和式（5）可得：

式中 R（x）即为要求的 CRC 校验码，xrk（x）+R（x）为发送端向接收端所发送的加入了CRC校验码的信息码，由式（6）可知 xrk（x）+R（x）能够被生成多项式 G（x）所整除。 故接收端对接受到的信息以同样的生成多项式G（x）生成其CRC校验码，如果为0，则表示数据传送过程中未出错，否则出错，应做出相应的处理。

2 CRC32算法介绍

CRC32规范中其生成多项式G（x）如下：

常用的CRC校验码生成算法包括串行比特型算法、查表型算法和并行算法[3-4]。串行比特型算法主要由一个32比特移位寄存器和异或单元组成。每输入一位串行数据，都会与移位寄存器中相应的位进行异或，异或结果保存在相应的位中，并循环移位一位，直到32位串行数据输入完毕，再进行32次循环移位将每一位寄存器中的数据依次输出，输出的32位数据即为CRC32校验值。其硬件实现框图如图l所示。

图1 比特型算法硬件框图Fig.1 Hardware diagram of bit calculation

串行比特型算法可以很容易通过带反馈的移位寄存器的硬件实现，其吞吐率可以达到200 Mbps，但是远远不能达到高速通信系统的要求。

对于查表法生成CRC校验码，要预先计算好所要的有效信息位，并存放信息位表中，然后按信息位的顺序计算好所有校验位，并存放于表中，待要使用时通过查表输出对于的CRC校验值。但这种方法需要较大的存储空间存储长度较大的CRC余数表，并且随着并行位数的增加，余数表的长度按指数增加，对于CRC32规范也不具有现实性[5]。

因此，SATA协议中需采用并行CRC32算法以达到3 Gbps的吞吐率。

3 CRC32并行算法推导

CRC32并行算法可由串行比特型算法推导而出。

令需进行校验的32位数据以Q0表示，32位移位寄存器初始值用M0表示即：

自反馈的移位运算可以采用状态转移矩阵表示，i+1次移位后寄存器的状态Qi+1与i次移位后寄存器的状态Qi之间的关系可通过状态矩阵A表示为：Qi+1=AQi，进一步又可得到第i次的状态Qi可通过初始状态Q0表示为：

式中状态转移矩阵A可由式（7）和CRC32串行实现框图推导得到[6]。首先32位数据串行输入，与移位寄存器相关位中的初始值进行模2加减运算，32次移位后数据输入完毕，即：

然后再进行32次移位，移位寄存器中的内容即为所求的CRC校验值，则：

综合式（11）和式（12）得：

由式（13）可知：CRC校验值只与CRC校验初始值M0和需校验数据Q0有关，其中A64和A32可以由MATLAB计算得出。通过计算，可以得出CRC校验最高位为：

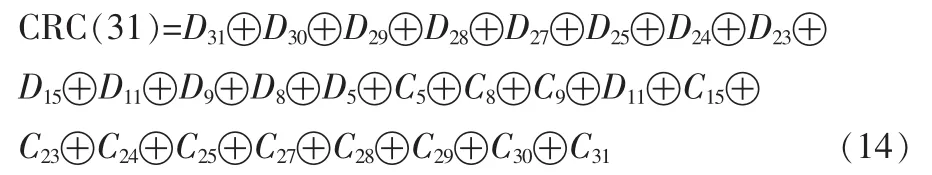
CRC32其他校验位都可以类推由式（13）得出。

4 SATA协议中CRC32算法实现

SATA总线主要由应用层、传输层、链路层和物理层组成，其中传输层主要用于传输数据命令，链路层则是对数据进行编码和解码以保证数据在链路中正确传输。SATA总线链路中的信息包含两种结构：原语（Primitive）和帧（Frame），两者都以双字为最小的单位，其结构如图2所示。

图2 SATA链路数据结构图Fig.2 Structure chart of the SATA link data

帧结构由多个双字组成，包括帧头（SOF）、帧数据、帧尾（EOF）和用于控制码流的控制原语HOLD原语和HOLDA原语。SATA协议中CRC校验模块需自动识别出数据流中的原语，并不计算这些原语的CRC值。在发送信息时，需要由帧数据生成CRC码，即所有非原语数据都要进行CRC编码，并且将生成的CRC值插入到帧尾（EOF）之前进行传输。在接受到数据时，需要对帧数据进行CRC校验，从而判断数据在链路中传输是否出错。在SATA协议中规定CRC校验初始值0x52325032，并且在帧头和帧尾中的数据不能超过2 046个双字。

SATA协议中CRC生成校验模块采用有限状态机来识别传输数据流中的原语，从而完成CRC值的生成与校验。其状态机结构图如图3所示。

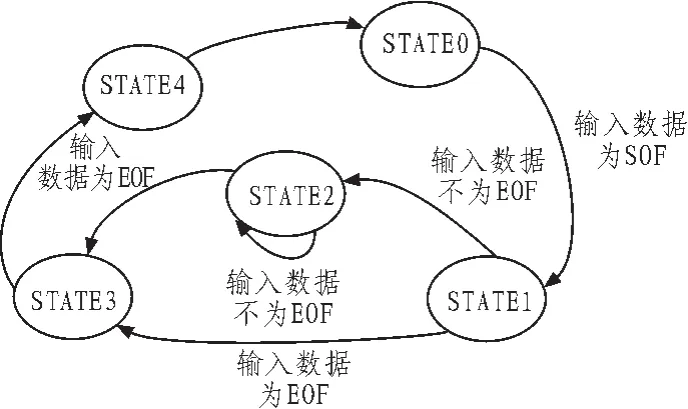
图3 CRC生成模块状态转换图Fig.3 State transition diagram of CRC generation module

其中状态STATE0检测帧头并装入STATE1状态；在STATE1中，当输入数据为帧尾时，则转入STATE3状态，否则转入STATE2状态，在STATE1状态下输出帧头，并设置CRC初始值为0x52325032h；在STATE2中，当输入为帧尾时，则转入STATE3状态，否则转入STATE2状态，对非原语数据进行CRC值生成，并保存到寄存器中，输出为数据或保持原语；在STATE3中输出最终的CRC值，并转入STATE4状态；在STATE4中输出帧尾，并转入STATE0状态等待下一次数据的输入。

输入一帧数据，并由式（14）进行计算，得出输入数据对应的CRC计算值如表1所示。

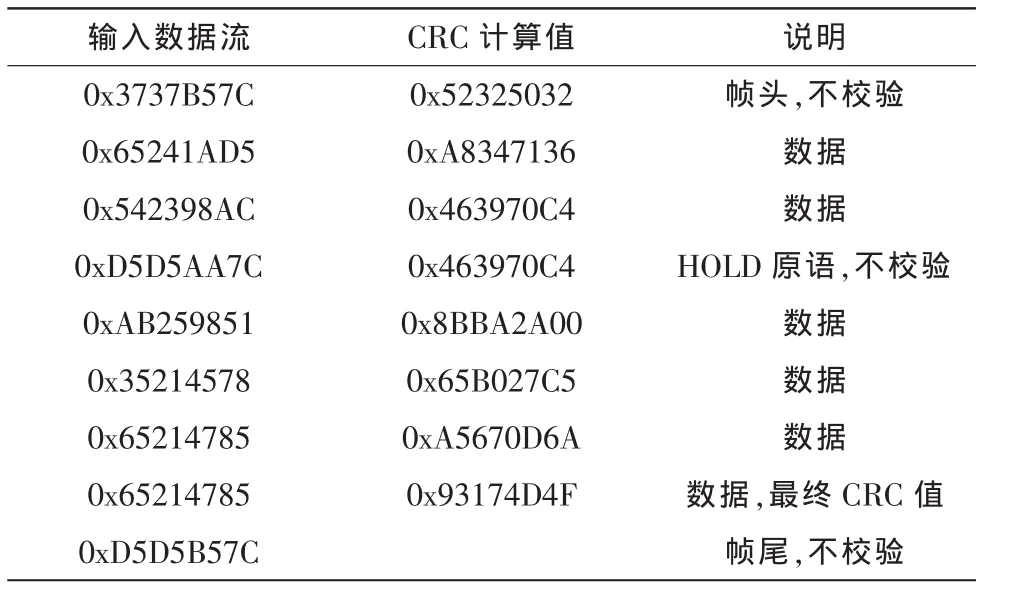
表1 输入数据流实例Tab.1 The examp le of input data flow

其对应的系统仿真结果如图4所示。

图4 系统仿真结果图Fig.4 Result of system simulation

仿真结果显示，CRC数据校验与表1中的理论值一致，CRC生成模块能够自动识别数据流中的原语和数据，并能有数据生成正确的CRC校验值。其中每双字数据生成CRC值仅需一个时钟周期，系统输出延时仅为一个时钟周期，相对于串行CRC生成算法，CRC32并行算法更能满足SATA协议对时钟频率的要求。

5 结束语

文中介绍了CRC校验原理和常用CRC32实现算法，并根据比特型算法推导出一种CRC32并行算法的实现方案，该方案实现简单，实现的并行算法相对于串行算法具有速度快，运算简单，并且易于硬件实现等优点。本文还将将CRC32并行算法与SATA协议相结合，实现了满足SATA协议规范的CRC生成和校验模块，并成功应用于SATAⅡ主控制器的设计中。

[1]黄维超，刘桥，黄初华.基于FPGA的循环冗余校验并行实现[J].信息技术，2009（6）:181-183.HUANG Wei-chao，LIU Qiao，HUANG Chu-hua.Inplementation of parallel CRC based on FPGA[J].Information Technology，2009（6）:181-183.

[2]叶懋，刘宇红，刘桥.CRC码的FPGA实现[J].重庆工学院学报：自然科学版，2007，21（3）:85-87.YE Mao，LIU Yu-hong，LIU Qiao.Implementation of CRC based on FPGA[J].Journal of Chongqing Institute of Technology：Natural Science Edition，2007，21（3）:85-87.

[3]范红旗，王胜，祝依龙.CRC编解码器及其FPGA实现[J].数据采集与处理，2006（21）:97-100.FAN Hong-qi，WANG Sheng，ZHU Yi--long.CRC coderencoder algorithm and its FPGA implemenation[J].Journal of Data Acquisition ＆ Processing，2006（21）:97-100.

[4]常天海，胡鉴.基于FPGA的CRC并行算法研究与实现[J].微处理机，2010（2）:45-48.CHANG Tian-hai，HU Jian.Applicating research of CRC parallel algorithm based on FPGA[J].Microprocessors，2010（2）:45-48.

[5]张树刚，张遂南，黄士坦.CRC校验码并行计算的FPGA实现[J].计算机技术与发展，2007，17（2）:56-58.ZHANG Shu-gang，ZHANG Sui-nan，HUANG Shi-tan.CRC parallel computation implementation on FPGA[J].Computer Technology and Development，2007，17（2）:56-58.

[6]郭熙业，苏绍璟，王跃科.并行CRC-32校验码生成算法研究及其实现[J].电子技术应用，2007（5）:121-123.GUO Xi-ye，SU Shao-jing，WANG Yue-ke.Applicating research of CRC-32 parallel generation algorithm[J].Application of Electronic Technique，2007（5）:121-123.

[7]张伟，陈锋，马军强.轨/姿控发动机脉冲后效冲量快速算法的研究及应用[J].火箭推进，2012（1）:51-56.ZHANG Wei，CHEN Feng，MA Jun-qiang.Research and application of fast algorithm for pulse residual impulse of divert and attitude control engine[J].Journal of Rocket Propulsion，2012（1）:51-56.