基于dq变换和S变换的电能质量扰动识别

王 鑫， 王 卓， 郑 璐

（哈尔滨理工大学 黑龙江 哈尔滨 150080）

随着电能质量敏感设备应用的急速增加，电能质量问题越来越受到电力部门与用户的关注。为了改善和提高电能质量，需要对电能质量扰动进行识别。实现电能质量扰动的正确分类，将有助于分析扰动产生的原因，找出合理的应对措施。

目前，不少学者已经提出了一系列有效的电能质量扰动识别方法，如用Hilbert-Huang变换对电力系统暂态信号进行分析[1]，用小波变换和二叉树结构对电能质量扰动进行分类[2]，用贝叶斯分类器对扰动信号进行分析[3]，用数学形态学的方法进行扰动检测与定位[4]，用分形方法对扰动信号进行检测[5]，用人工神经网络[6]、支持向量机[7]对扰动进行分类和识别等。上述方法有的算法复杂计算量大，有的需要大量的样本进行训练，较难用于实际检测中。S变换是连续小波变换和短时傅立叶变换的继承和发展，同时具有很好的抗噪性，因此成为近几年的一个研究热点。

文中利用dq变换电压有效值波形特征，对测量信号采用单相延迟60°构造三相，进行dq变换，实现对第一类扰动的识别；通过S变换后的S矩阵，提取信号的特征量，对第二类扰动进行识别。本方法可作为研究配电系统电能质量监测网络的基础，以实现电能质量扰动的实时监测与自动识别。

1 扰动识别原理

1.1 dq变换

文献[8]阐述了单相延时60°构造三相的dq变换法，并得到dq变换结果为：ud=Ua（Ua为a相电压的有效值），uq=0。

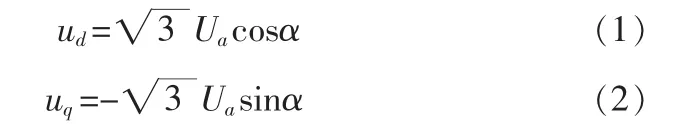
式中α为相位移。将dq变换结果进行处理，可得电压有效值为：

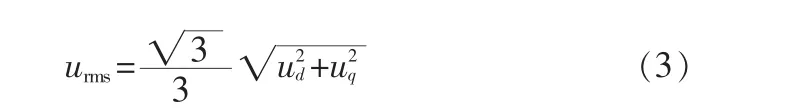
对无扰动纯正弦电压urms=Ua，因此采用该方法可瞬时求取电压的有效值。

1.2 S变换

S变换是一种时频可逆的分析方法，它引入了宽度和频率成反比变换的高斯窗，并具有与频率相关的分辨率。因此，S变换既有小波变换多分辨率分析的特点，又有短时傅里叶变换的单频率独立分析的能力，同时又避免了短时傅里叶变换窗函数选择的问题。

给定一连续的时间信号x（t），其S变换为：

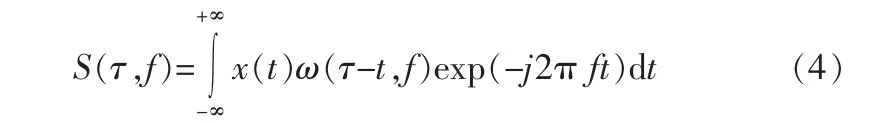
式中 ω（τ－t，f）为高斯窗函数，τ为控制高斯窗口在 t轴位置的参数，1/|f|为尺度因子。 信号 x（t）可以由其 S变换 S（τ，f）很好地重构，其S逆变换为：

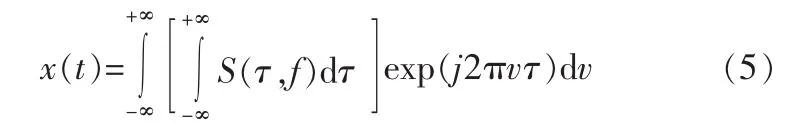
由于信号x（t）的S变换与其傅里叶变换X（f）之间存在如下关系：

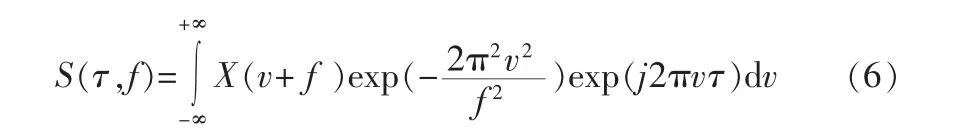
令f=n/NT，τ=kT，其中T为采样时间，N为总采样点数。由式（6）可以得到S变换的离散表示形式：

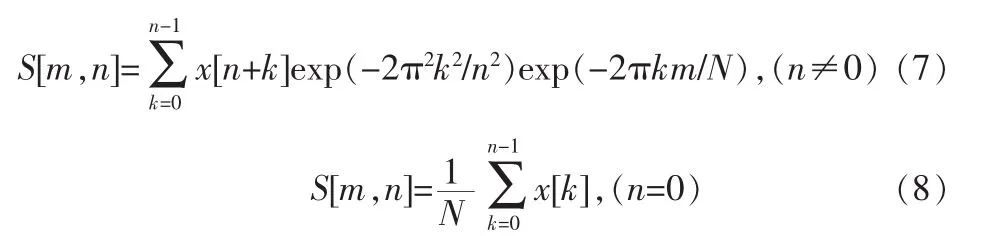
S变换的结果为一个复时频二维矩阵，记为S矩阵。将S矩阵各元素求模记为S模矩阵，某一时间和频率处S变换的模值就是S矩阵中相应元素的幅值。其行向量为信号某一频率的幅值随时间变化的分布，列向量为信号某一采样时刻的幅值随频率变化的分布。

2 扰动识别方法

该文提出一种将dq变换和S变换相结合的电能质量扰动分层识别方法，识别流程如图1所示。

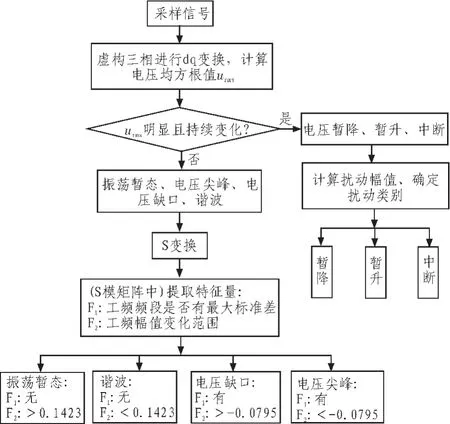
图1 扰动识别流程图Fig.1 Flow diagram of disturbance identification

首先，根据扰动信号电压有效值变化特征，初步将扰动信号分为两类。即电压暂降、暂升和中断为第一类；振荡暂态、电压尖峰、电压缺口和谐波为第二类；第二，对采样信号进行基于虚构三相的dq变换，计算信号的电压均方根值urms，如果urms有明显且持续的变化，则为第一类扰动信号，并进一步计算扰动的幅值，确定扰动类别是电压暂降、暂升还是中断；第三，对第二类扰动进行S变换，通过从变换后得到的S模矩阵中提取特征量来识别第二类扰动类别。用统计分析的方法提取扰动信号S变换结果的时频信息，提取的特征量为F1：工频频段是否有最大标准差，F2：工频幅值变化范围。

3 MATLAB仿真及结果

利用文献[9]提供的扰动信号模型产生扰动信号样本。设信号的频率为工频50 Hz，采样频率为1 600 Hz，采样点数为320点，那么每周期采样的点数为1600/50=32个点，共采样320/32=10个周期。

对第一类扰动信号进行dq变换，如图2所示。从图2中发现电压暂降、暂升、中断dq变换得到的urms的幅值均有明显变化，且变化后持续一段时间，然后通过有效值的大小区分三者（电压暂降：0.1～0.9 p.u.；暂升：1.1～1.8 p.u.；中断：小于 0.1 p.u.）。

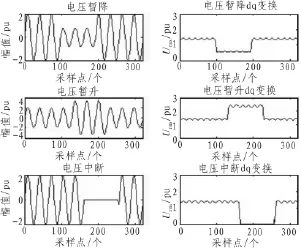
图2 第一类扰动的dq变换仿真图Fig.2 Simulation diagram of dq conversion of first type

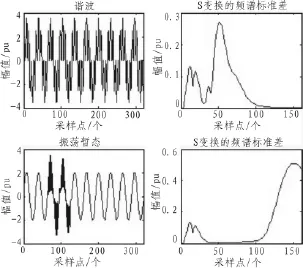
图3 谐波和振荡暂态的S变换仿真图Fig.3 Simulation diagram of S transform of harmonic and oscillation transient

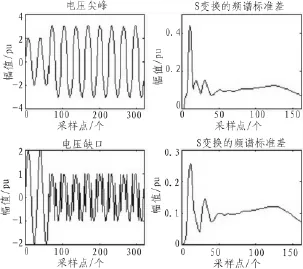
图4 电压尖峰和电压缺口的S变换仿真图Fig.4 Simulation diagram of S transform of voltage spike and gap

对第二类扰动信号进行S变换，如图3，4所示。从图3，4中发现第二类扰动信号经S变换后，得到的频谱标准差曲线中，谐波和振荡暂态的S矩阵的最大标准差不在工频频段；而电压尖峰和电压缺口的却在工频频段。同时，再通过各自S矩阵的工频幅值变化范围，就可将第二类扰动一一区分开来。

通过改变扰动的持续时间、幅值和起始相位角，同时均添加20 dB的噪声，对各种扰动信号均产生50个样本，共350个样本，应用本文提出的方法进行识别分类，结果见表1。

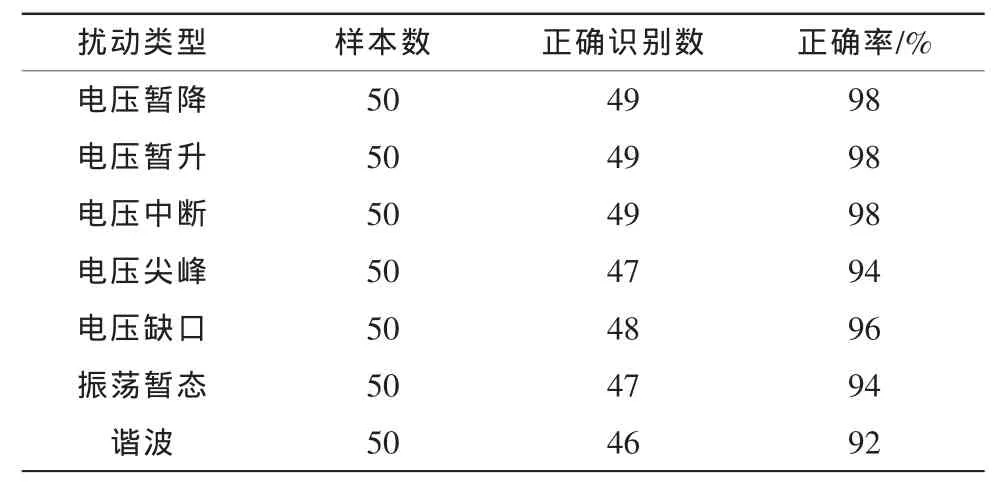
表1 扰动识别结果Tab.1 Result of disturbance identification

由表1可知，文中的方法具有较高的分类辨识率，取得了良好的效果。

4 结 论

文中针对电能质量检测和识别的要求，提出了一种基于dq变换和S变换的电能质量扰动识别的方法。仿真计算结果表明，该方法能够对7种电能质量扰动信号进行有效的分类辨识，准确度高、响应速度快、结构简单且抗噪声能力强。

[1]聂永辉，高磊，唐威.Hilbert-Huang变换在电力系统暂态信号分析中的应用[J].电力系统及其自动化学报，2009，21（4）:63-69.NIE Yong-hui， GAO Lei， TANG Wei.Application of Hilbert-Huang transform on analysis of transient signal in electric power system[J].Proceedings of the CSU-EPSA，2009，21（4）:63-69.

[2]冯浩，谢刚文，郑贺伟，等.基于小波变换和二叉树结构的电能质量扰动分类[J].低压电器，2011（5）:35-38.FENG Hao， XIE Gang-wen， ZHENG He-wei， et al.Power quality disturbances classification based on wavelet transform and binary tree architecture[J].Low Voltage Apparatus，2011（5）:35-38.

[3]舒泓.电能质量扰动检测和分类问题的研究[D].北京:北京交通大学，2008.

[4]王丽霞，何正友，赵静.基于数学形态学的电能质量扰动检测和定位[J].电网技术，2008，32（10）:63-68.WANG Li-xia， HE Zheng-you， ZHAO Jing.Detection and location of power quality disturbance based on mathematical morphology[J].Power System Technology，2008，32 （10）:63-68.

[5]王晶，束洪春，陈学允.动态电能质量的分形指数小波分析方法[J].中国电机工程学报，2004，24（5）:40-45.WANG Jing， SHU Hong-chun， CHEN Xue-yun.Fractal exponent wavelet analysis of dynamic power quality[J].Proceedings of the CSEE，2004，24（5）:40-45.

[6]谷湘文，高培生，吴为麟.基于S变换和神经网络的电能质量多扰动分类识别[J].机电工程，2007，24（9）:46-49.GU Xiang-wen， GAO Pei-sheng， WU Wei-lin.Classification and recognition of power quality multi-disturbance based on S-transform and neural networks [J]. Mechaical &Electrical Engineeringmagazine，2007，24（9）:46-49.

[7]黄南天，徐殿国，刘晓胜.基于S变换与SVM的电能质量复合扰动识别[J].电工技术学报，2011，26（10）:23-30.HUANG Nan-tian， XU Dian-guo， LIU Xiao-sheng.Identification of power quality complex disturbances based on S-transform and SVM [J].Transactions of China Electrotechnical Society，2011，26（10）:23-30.

[8]徐永海，肖湘宁，杨以涵，等.基于dq变换和ANN的电能质量扰动辨识[J].电力系统自动化，2001（14）:24-27.XU Yong-hai， XIAO Xiang-ning， YANG Yi-han， et al.Power quality disturbance identification using dq conversion based neural classifier[J].Automation of Electric Power Systems，2001，（14）:24-27.

[9]Youssef A M，Abdel-Galil T K，El-Saadany E F，et al.Disturbance classification utilizing dynamic time warping classifier[C]//IEEE Transactions on Power Delivery，2004:272-278.