一种新的自适应数字水印算法
2012-06-09王景中张哲铭
王景中,张哲铭
(北方工业大学 信息工程学院,北京 100144)
计算机和网络技术迅猛发展,信息媒体的数字化使得信息的使用和传播更加便利和快捷,但是另一方面数字产品的不安全性也变得越来越严重,如:非法复制,篡改等。所以利用数字水印来保护多媒体产品已经成为信息安全保护技术的一个重要的分支。此项技术的研究的目的是在原创作者的作品中添加不可见的标记,用来对作品所有者的所有权益进行保护。
根据嵌入域不同,水印算法大体分为空域和变换域两种,变换域水印算法嵌入的水印信息较空间域大,并且具有良好的鲁棒性,因此成为水印算法研究的主流方向。近些年来,有关奇异值分解SVD(singular value decomposition)的数字水印的方案引起了人们的关注。
在国内Liu和Tan最早提出基于奇异值分解的数字水印的方案,之后又有许多专家和学者在这些理论的基础上改进了SVD奇异值分解算法,比如:DCT-SVD域、DFTSVD域等。大部分文献中提出了保留了与水印相关的矩阵U和V,但是左右矩阵与提取的水印之间存在很大的相关性,即使能提出来水印,也存在相当大的虚警率,文献[1]提出了利用SVD在小波分解中的应用,基于分块自适应技术实现数字水印嵌入和提取,有比较好的鲁棒性,文献[2]提出了利用载体图像SVD正交分解的U矩阵和嵌入图像的U矩阵的相似性作为判断条件。文献[3]还提出一种结合人类视觉技术计算嵌入强度,实现水印信息嵌入。有些算法没有对数字水印做预处理,同时也没考虑到HVS,所以存在缺陷[4],在文献[5]中着重研究了水印信息预处理过程,提出了一种图像分块后像素值方差和像素点与4邻域灰度差值相结合的最佳置乱度计算方法,实验证明置乱程度与主观视觉效果一直,文献[6]创新的提出了对原始载体图像分块做DCT变换处理,将每个分块的AC(直流分量)将组成一个新的矩阵SVD分解后,将水印信息嵌入其中。
1 数字图像水印相关理论
1.1 Arnold置乱方法
考虑到水印图像各像素点之间存在紧密的相关性,为了避免图像线性密码攻击,将图像按照一定规律将图像进行置乱。
本文首先对水印进行置乱预处理来增加水印的安全性,这里采用了著名的数学家Arnold在研究遍历理论是提出的Arnold变换。
Arnold变换如下方法:
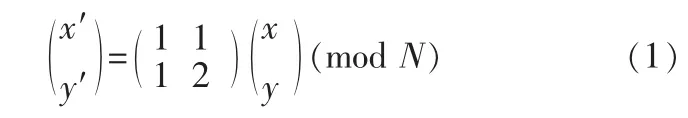
实现图像中任意给定位置(x y)1≤x,y≤N,这里的N指的是图像的高或者宽,该变换表达式满足,其目的是加密后的图像通过变换后可恢复出原图像。其中(x y)和(x′y′)满足:

选取合适的参数是为了提高图像置乱加密的安全性,可以避免线性密码攻击。
1.2 SVD奇异值分解理论
假设C=M*N矩阵,U是M*M矩阵,其中U的列为CCT的正交特征向量,V为N*N的矩阵,其中V是CCT的特征向量,再假设r为C矩阵的秩,则存在奇异值分解:

其中CCT和CTC的特征值相同,为λ1…λr
其余的元素为0,如图1所示:
图1 SVD奇异值公式分解Fig.1 SVD singular value formula decomposition
式中,U∈RM*M,V∈RN*N是正交阵,S是 ∈RM*N是非对角线上的元素都为 0 的矩阵,S=diag(l1,l2,l3,…lr),其元素满足l1>l2>l3>,…lr。
从数学的角度分析:CCT和CTC的特征值相同,说明特征值在矩阵变换过程保持稳定。
从图像的角度分析:奇异值具有较强的稳定性,图像奇异值体现图像信息的内蕴特性,图像发生较小变化时,图像奇异值不会发生较大变化而且图像的视觉效果依然很好,旋转、缩放、平移等几何攻击不会使图像的奇异值有太大的影响。这样利用图像的奇异值分解嵌入水印信息可以减少图像失真和提高图像的不可见性和鲁棒性。
1.3 JPEG图像压缩特性
JPEG对图像压缩的核心算法是DCT变换编码,为了适应用于单色图像或者彩色图像,JPEG对每一个图像分量单独编码。对于JPEG压缩前和压缩后的图像的比值,我们称之为JPEG压缩比,利用JPEG压缩比可以对图像一小块图形进行分析和处理。JPEG提供了4种工作模式:
1)顺序编码。每一个图像分量按从左到右,从上到下扫描,一次扫描完成编码。
2)累进编码。图像编码需多次扫描完成,图像有粗糙到清晰。
3)无失真编码。保证解码后完全精确地恢复源图像的采样值。
4)分层采样。图像在多个空间分辨率进行编码。
因此不同的工作模式,不同的压缩比也不一样,针对不同的压缩比,在数字水印嵌入过程中采用不同的嵌入调节因子,使嵌入水印后的图像产生良好的视觉效果。
2 基于奇异值分解的数字水印算法
2.1 图像水印嵌入强度的分析
首先对图像进行预处理,将图像区域划分为L*L个互不重叠的子块,然后通过JPEG压缩比计算嵌入强度。
由于JPEG对图像的压缩有很大的伸缩性,图像质量与比特率的关系如下:
1)1.5~ 2.0 比特/像素:
与原始图像基本无区别,仿真调节因子为1.3
2)0.75 ~ 1.5比特/像素:
图像质量很好,仿真调节因子为1.2
3)0.5 ~ 0.75比特/像素:
图像质量比较好,仿真调节因子为1.0
4)0.25~0.5比特/像素:
图像质量一般,仿真调节因子为0.8
2.2 嵌入算法
1)将水印图像置乱,经过两次小波分解后获取二阶低频分量,并将其进行cdma编码调制。
2)将原始载体图像,分解成互不重叠的8×8的图像块,并对图像块进行DCT变换,然后在做SVD奇异值分解,选取分解的S矩阵,同时通过JPEG压缩特性计算分块的调节因子。
3)将水印调制后的 CDMA 序列按照公式(5)、公式(6)加入到载体图像的每个分块的分解后的S矩阵中去。
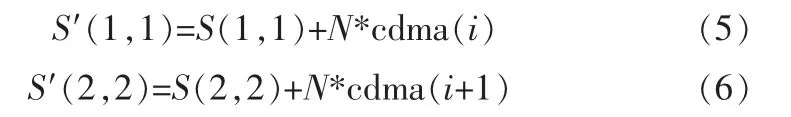
S′为嵌入水印后图像的S矩阵,S为原始图像的S矩阵,cdma为水印信息cdma调制的信息。
2.3 提取算法
1)将嵌入水印后的图像分块提取,每个8*8的图像块做DCT变换、SVD分解选取S_em矩阵 。
2)S_em与原始图像DCT变换,SVD分解的S矩阵按照公式(7)、公式(8),提取 cdma 序列。
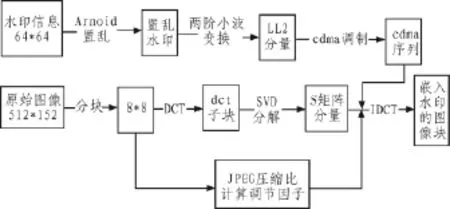
图2 水印嵌入算法流程图Fig.2 Watermark embedding algorithm flow diagram
3)将cdma序列还原成比特流序列,然后反DWT重构提取的水印图像。

按照水印置乱的计算出水印图像W’。用归一化相关系数NC检查水印的相似度
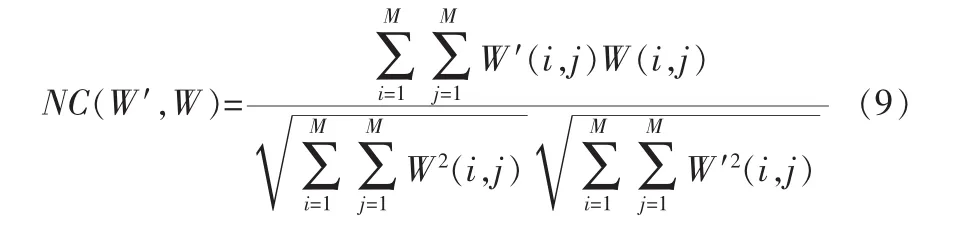

图3 水印提取算法流程图Fig.3 Watermark extraction algorithm flow diagram
3 仿真结果分析
为了检验本算法的可行性,采用在Matlab 2011a版本平台上做仿真实验。本算法使用的图片是512*512的lena.bmp灰度图像(如图4所示)和64*64的水印图像(如图5所示)。

图4 载体图像Fig.4 Carrier image

图5 嵌入水印后图像Fig.5 Watermarked image

图6 水印图像Fig.6 Watermarking images

图7 原始图像提取Fig.7 Extracted watermark

图8 放缩30%攻击Fig.8 Scaling attack(30%)

图9 旋转90度Fig.9 Rotation(90°)
嵌入水印后图像的PSNR=35.03 dB。在为受到攻击的情况下,能够完全正确的提取水印的NC=0.937 7。
为了检测算法的鲁棒性,本算法使用StirMarkBenchnark对嵌入水印的后的图像分别进行了JPEG压缩、PSNR加噪、Rescale放缩、Rotation旋转、中值滤波等。采用峰值性噪比(PSNR)来衡量提取水印图像和原始水印的相关性。用归一化互相关系数(NC)来衡量提取水印和原始水印的相关性。

图10 JPEG压缩Fig.10 JPEG compression

图11 中值滤波攻击Fig.11 Median filtering attack

图12 剪切75%Fig.12 Cutting(75%)

图13 加噪90%Fig.13 Add Noising(90%)

图14 旋转剪切Fig.14 Rotating cutting
实验结果见表1.

图15 PSNR攻击Fig.15 PSNR attack

表1 图像水印的相关攻击测试结果Tab.1 image watermark attack test results
对嵌入水印的图像加各种攻击:PSNR (如图15所示)、JPEG压缩(如图 10)、添加噪声(如图 13所示)、滤波(如图11所示)、缩放(如图 8所示),旋转(如图 9所示),剪切(如图12所示),旋转剪切(如图14所示)等,从表1可以看出本算法对JPEG压缩、添加噪声、滤波、放缩、旋转等具有较高的鲁棒性。尽管在攻击下提取水印信息有一定的干扰,但是人眼还能较好的分辨出水印信息,从而说明本算法保持水印信息具有较好的鲁棒性。
4 结 论
本文算法借鉴了以往论文利用图像奇异值分解特征值强稳定性在图像经过离散小波变换后的图像中完成了水印的嵌入和提取过程。本算法的优点是在水印图像二阶小波分解基础上,将低频子带区域信息嵌入到原始载体图像经过奇异值分解后的S矩阵中,同时根据图像的源图像的压缩比等图像的相关特性选择最佳的调节因子,对水印图像小波变换的低频分量进行cdma编码调制,提取水印时采用cdma解调解码使之增加图像的鲁棒性和安全性,此外,本算法属于非盲提取。
[1]赵敏,王慧琴,卢麟.基于分块SVD自适应数字水印算法[J].计算机工程与设计,2011,32(4):84-86.ZHAO Xia,WANG Hui-qin,LU Ling.Adaptive digital watermarking algorithm based on block and SVD[J].Computer Engineering and Design,2011,32(4):84-86.
[2]钱华明,于鸿越.基于SVD-DWT域数字图像水印算法[J].计算机仿真,2009,26(8):457-459.QIAN Hua-ming,YU Hong-ji.Digital image watermarking algorithm based on the SVD-DCT[J].Computer simulation,2009,26(8):457-459.
[3]徐慕容,樊锁海.一种新的基于奇异值分解的图像数字水印算法[J].计算机仿真,2011,28(5):291-341.XU Mu-rong,FAN Suo-hai.A new image watermarking algorithm based on[J].Computer simulation,2011,28 (5):457-459
[4]肖俊,王颖.基于块奇异值分解的水印算法研究[J].中国科学院研究生院学报,2006,23(3):207-209.XIAO Jun,WANG Yin. Block-based SVD of the watermarking algorithm[J].Graduate School Journal of the Chinese Academy of Sciences,2006,23(3):207-209.
[5]黄永良.二值图像Arnold变换的最佳置乱[J].计算机应用,2009,40(2):66-69.HUANG Yong-liang.The best image scrambling degree of binary on Arnold transform.Journal of Computer Application,2006,23(3):207-209.
[6]王奔.基于DWT-DCT-SVD的图像数字水印算法 [D].北京:北京邮电大学,2010:203-205.
