BM模式匹配算法的研究和改进
2012-06-09揣锦华
揣锦华,郑 景,关 锐
(长安大学 信息工程学院,陕西 西安 710064)
串的模式匹配是串的一种很重要的运算,它一直都是计算机科学领域研究的焦点问题之一。串的模式匹配在众多领域被广泛的应用,如:拼写检查、搜索引擎、计算机病毒特征码匹配、入侵检测、数据压缩以及DNA序列匹配等,都离不开模式匹配算法。
所谓模式匹配就是在大量的文本串中查找模式串(一个给定的字符串)的一个或者多个匹配的过程。对于文本串为T=T0T1…Tn-1,长度为 n;模式串 P=P0P1…Pm-1,长度为 m。 如果在T中找到P的出现则表示匹配成功,否则匹配失败。
关于模式匹配的算法有很多,比较著名的有2个:KMP算法和Boyer-Moore算法[1](简称BM算法)。其中 KMP算法实现较为复杂,且效率有限。相比之下,Boyer-Moore算法实现更为简单,且在英文文本及模式较长的情况下,其效率一般是KMP算法的3~5倍,因此其应用更为广泛。
目前对于BM算法的改进算法有很多,但大体上改进都很有限,且稳定性并不尽如人意。下面将会对经典BM算法,以及目前比较流行的两种改进的BM算法进行简单的介绍,然后提出2点改进意见。旨在提升其效率的同时极大的提高其稳定性,最后通过具体的实验进行比较、验证。
1 现有的BM系列算法简介
1.1 经典BM算法
经典 BM(Boyer-Moore)算法[1]的基本思想是:开始时,将文本串T(长度为n)与模式串P(长度为m)左对齐,然后从模式串的最后一个字符Pm-1开始,从右至左依此与文本串的相应字符 Tm-1Tm-2…T0进行比较;当某次比较 Ti与 Pi不匹配时,模式串向右滑动一段距离后 k,开始执行由 Pm-1与 Ti+k-1起,从右至左的匹配检查,依此类推直到找到一个完整匹配或者全文搜索完毕为止。
经典BM算法在每次的比较匹配失败后会采用两种启发式规则来决定下一次匹配的位置 (即向右移动的距离),即:坏字符规则(BadChar)和好后缀规则(GoodSuffix):
1)好后缀规则(GoodSuffix)
在BM算法从右向左扫描的过程中,若发现某个字符不匹配的同时,已有部分字符匹配成功,则按如下2种情况讨论:
①如果在P中位置t1处已匹配部分P′在P中未匹配部分的某位置t2也出现,且位置t2的前一个字符与位置t1的前一个字符不相同,则将P右移,使t2对应t1方才所在的位置。
②如果在P中任何位置已匹配部分P′都没有再出现,则找到与P′的后缀P″相同的P的最长前缀x,向右移动P,使x对应方才P″后缀所在的位置。
即:P中的已匹配部分或已匹配部分的后缀子串Ps+1…Pm与P中尚未进行比较部分中的某一子串Pj-s+1…Pm-s相同,则P右移s位。如公式(1)所示。其中Shift(j)为P右移的距离,m为模式串P的长度,j为当前所匹配的字符位置,s为t1与t的距离(以上情况1)或者x与P″的距离(以上情况2)。

2)坏字符规则(BadChar)
在BM算法从右向左扫描的过程中,若发现某个字符x不匹配,则按如下两种情况讨论:
①如果字符x在模式P中没有出现,那么从字符x开始的m个文本显然不可能与P匹配成功,直接跳过该区域即可。
②如果x在模式P中出现,则以该字符进行对齐。
设 dest(x)为 P右移的距离,m为模式串 P的长度,max(x)为字符x在P中最右位置,数学公式表示公式(2)所示。

BM算法使用上述坏字符规则和好后缀规则计算得到的移动值中的大者来向右移动模式P到新的比较位置。实践证明在大字母表(相对于模式长度)情况下,BM算法效率非常高。
1.2 BMH算法
在实际应用中,BM算法的BadChar应用次数远远超过GoodSuffix,BadChar在匹配过程中起到移动指针的主导作用。因此在实际应用中,只使用BadChar也非常有效。为此,1980年Hompool提出了BM算法的简化改进算法,即BMH算法[2]。
BMH算法的基本思想是:将匹配失败与计算右移量独立。计算右移量时不关心文本中哪个字符匹配失败,而是直接使用与模式串最右端的字符对齐的那个文本字符Ti+m-1在模式串P中出现的位置来决定右移量。此时其移动距离可由上述公式1求得,只不过此时公式中的x变成了Ti+m-1而已。即移动距离为dest(Ti+m-1)。所以当Tm+i-1不在模式串中出现时,模式串获得最大移动距离m。
1.3 BMHS算法
1990年,Sunday在BMH算法的基础上又提出了一种改进的算法—BMHS算法[3],其主要的改进思想是:在一次匹配失败时,考虑下一个字符Tm+j的情况。即利用与模式串P对齐的文本字串的下一个字符Tm+j来决定右移量的大小。如果Tm+j不在模式串中出现时。则直接跳过该字符,即将模式串P可以达到最大的移动距离m+1。如果Tm+j出现在模式串中,则将该字符在模式串P中最右侧出现的位置与文本中的字符Tm+j对齐,然后进入下一次匹配。即移动距离skip=m-last(Tm+j)。 当 last(Tm+j)=-1,即 Tm+j不在模式串中出现时,模式串获得最大移动距离m+1。
试验表明,一般情况下BMH以及BMHS算法比BM算法有更好的性能[4-5]。
2 改进的IBMH(Im proved BMH)算法
2.1 IBMH算法的思想
从上述算法可以看出,BMH只考虑了文本串T一次匹配的最后一个字符Ti+m-1在模式串P中出现的情况,而BMHS算法则只考虑了文本串的一次匹配的下一个字符Ti+m在模式串P中出现的情况。二者都有一个共同的缺点,就是如果文本串的比较字符在模式串P中多次出现时,二者没有太大的差别,且效率也没有太大的提高。
根据对以上算法的分析,结合BM、BMH算法和BMHS算法的优点,在考虑失配位置字符产生的最大移动距离dest1的同时,考虑字符串最后一个字符及其下一字符的组合特性所产生的最大移动距离dest2。最终移动距离为二者中的最大者。
当发生失配时,若模式失配位置为i,文本串失配位置为j,失配字符为c。则由失配字符引导的最大移动距离dest1如下所示:

dest2由BMH以及BMHS的组合决定,即通过Ti+m-1Ti+m在模式串P中是否出现以及出现的位置决定。为此我们可以定义函数dest2(c1c2),用于计算有字符串Ti+m-1Ti+m所确定移动距离。其定义如下所示。
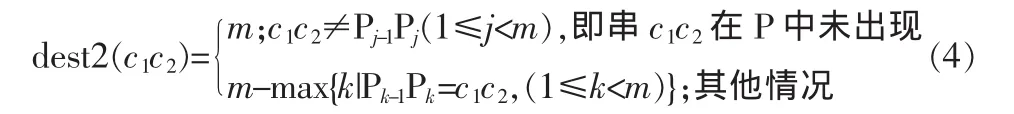
最终移动距离skip=max{dest1,dest2}。一种拿空间换时间的做法能够更有效地提高改算法的效率,即对于给定的模式串P,在开始匹配之前将字母表中的所有c的dest1的值都计算出来并放在一张表中,在使用时就可以直接从表里面取,这样就省去了很多的计算操作。
2.2 BM算法的复杂度分析
由上文所述可知,BM、BMH、BMHS、IBMH算法的最大移动量分别是m、m、m+1、m+1。影响模式匹配算法效率的除了最大移动量外还有产生最大移动量的概率和窗口比较次数等。对于BM、BMH及BMHS算法,它们的最大移动量均发生在一次匹配的末位字符或者其下一个字符在模式串中未出现的情况下。而对于IBMH算法,其最大移动量发生在这两个字符的组合串在模式串中未出现的情况下。显然,两个字符的组合串在模式串中出现的概率要比一个字符在模式串中出现的概率低很多。因此IBMH算法获得最大移动距离的概率要比其他几种算法的概率大很多。
尽管在最坏情况下,BM算法的时间复杂度均为O (nm+|Σ|)。但是BM算法是平均时间复杂度可以达到O(m+n+|Σ|)[6]。可见,在最好情况下,BM算法的时间复杂度将是低于线性的。在实际应用中,BM算法往往能够跳过很大一部分文本。此外,由于IBMH算法在进行失配跳跃时不仅考虑了还未进行比较的字符出现的情况,还将已经完成的匹配结果考虑了进去,因此其稳定性方面较其他几种算法也有很大提高。
3 实验测试及结果比较
实验环境为Windows XP Professional操作系统,系统的配置为Intel P4 CPU 2.8 GHz,内存 512M,编译器采用Microsoft Visual C++6.0。4种算法均用C语言编写,实验采取5.05 MB的英文文本内容作为正文串。
试验主要对上述4种算法在进行匹配时的模式串移动次数、字符的比较次数以及同样进行10 000次匹配所花费的时间进行了采集,采集后的比较结果分别如图1~3所示:(其中横轴为模式串字符个数,图1纵轴为模式串移动次数,图2纵轴为字符比较次数,图3纵轴为完成1万次匹配所耗费时间,单位为ms)

图1 模式串移动次数Fig.1 Number of pattern string moves

图2 字符比较次数Fig.2 Number of character comparisons
从上述实验结果可以看出,在同等条件下,4种算法在模式串移动次数、字符比较次数、以及完成1万次匹配所用运行时间上,IBMH算法在大多数情况下其性能明显要比其他3种算法要好很多,尤其是在稳定性方面,IBMH算法要比其他算法更加稳定。
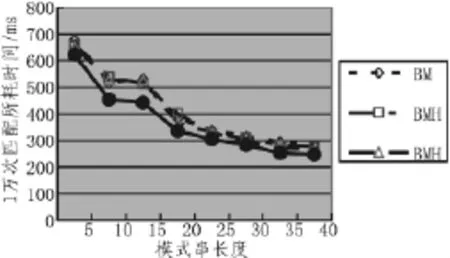
图3 10000次匹配所用运行时间Fig.3 Time-consuming of 10000 times match
4 结束语
目前对于BM算的改进算法有很多,且各有特点。在对不同文本模式进行匹配时也有各自的优势。文中在对已有的3种BM算法的研究的基础上提出了两点改进意见,并通过实验验证表明:该改进算法在性能及稳定性上确实有一定的提高。因此,在模式匹配算法的应用领域中,该算法也必将能带来更好的性能。
[1]Boyer R S,Moore J S.A fast string searching algorithm[J].Communications of the ACM,1977,20(10):762.
[2]Nigel H R.Practical fast searching in strings[J].Software-Practice and Experience,1980,10(6):501-506.
[3]Daniel M S.A very fast substring search algorithm[J].Communications of the ACM,1990,33(8):132-142.
[4]杨薇薇,廖翔.一种改进的BM模式匹配算法[J].计算机应用,2006,26(2):318-319.YANG Wei-wei,LIA0 Xiang.Improved pattern matching algorithm of BM[J].Computer Applications,2006,26(2):318-319.
[5]袁静波,郑吉森,丁顺利.一种BM模式匹配算法的改进[J].计算机工程与应用,2009,45(17):105-107.YUAN Jing-bo,ZHENG Ji-sen,DING Shun-li.Improvement of BM pattern matching algorithm[J].Computer Engineering and Applications,2009,45(17):105-107.
[6]古德里奇,塔玛西亚.算法分析与设计[M].霍红卫,译.人民邮电出版社,2006.
