基于改进网格聚类的动态雷达信号分选算法
2012-06-08陈维高张国毅
陈维高,张国毅
(空军航空大学,长春 130022)
0 引言
雷达信号分选是指从侦察接收机输出的随机交叠脉冲流中分离出各部雷达信号的过程,也就是脉冲信号去交错的过程。它是现代电子侦察系统的关键技术,同时也是电子情报侦察系统(ELINT)和电子支援系统(ESM)的重要组成部分。然而,随着雷达数目的急剧增加和信号形式的日趋复杂,使得现代雷达信号分选任务面临巨大的挑战。目前,应用到雷达信号分选的主要方法有模板匹配法[1]、直方图分选法(CDIF、SDIF)[2-3]和平面变换技术[4]等。在现代高密度复杂信号环境下,这些算法存在着运算量巨大、无法满足实时性需要的问题。因此,亟需一种运算量小、实时性好的分选算法来稀释高密度脉冲流,完成对侦察信号的初步分类,减少后续分选任务的负担。
近年来聚类分析技术广泛应用于雷达信号分选中,并取得了较好的效果。其中,由于网格聚类算法[5]实时性好,可以在无先验知识的条件下充分利用数据集自身的密度连通性完成聚类,且该算法的处理时间独立于数据对象的数目,因此非常适合处理数据量巨大且对实时性要求高的雷达信号分选任务。然而,传统网格聚类算法存在密度阈值设置不够合理、对边缘数据处理不完善、聚类精度较低的问题[6]。针对以上问题,本文提出了一种基于改进网格聚类的动态雷达信号分选算法。该方法首先将CluStream 聚类算法中的双层框架引入雷达信号分选系统,增强了分选系统的实时性,然后通过双密度阈值策略和边缘稀疏网格优化处理,改进了传统网格聚类算法。仿真结果表明,该方法具备较高的抗干扰能力和聚类精度,取得了较好的分选效果。
1 动态信号分选框架
数据流聚类是针对连续数据流的聚类分析方法,如果把接收机不断输出的雷达侦察数据看作数据流,则雷达信号分选就可以转化为数据流聚类的问题。本文将经典数据流聚类算法CluStream[7]的双层框架引入雷达信号分选,并结合文献[8]提出的动态信号分选框架来设计信号分选系统。如图1所示,动态信号分选框架主要分为两个部分:一是在线层不断将侦察数据转化为概要数据结构信息,并定时存储;二是离线层直接访问暂存数据库,利用概要信息完成信号分选。
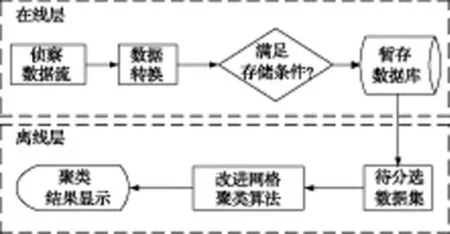
图1 动态信号分选框架图
1.1 在线层
侦察接收机侦收到的数据不断涌入,形成侦察数据流,此时数据流中包含大量的数据信息,需要对其进行数据转换以获得离线部分所需的概要数据结构信息。在满足一定的存储时间条件下,将数据转换后形成的概要数据结构信息存储到暂存数据库中,以供离线层调用。
1.2 离线层
根据具体的分选需求从暂存数据库中调取相应的概要数据信息,然后利用改进网格聚类算法完成信号的分选任务,并显示出聚类结果。
将分选系统设置成双层框架结构,可以在接收机输出侦察数据的同时将数据转化为概要数据结构信息,不用直接处理接收机输出的海量数据,相比传统的静态分选方法,节省了整个分选过程所用的时间,增加了分选系统的实时性[9]。
2 网格聚类算法
2.1 网格单元
将参数空间D=(D1,D2,…,Dd)的每一维划分为K个区间。这些区间按照该维参数值的大小顺序排列,则整个参数空间被分成有限个不相交的矩形(或超矩形)单元。这种划分后的单元称为网格单元,使得数据集中所有数据信息都能投影于这些网格单元中去。
2.2 相邻网格单元
当d 维参数空间中的两个网格单元U1、U2存在公共顶点或者公共边界时,称这两个网格单元为相邻网格单元。
2.3 网格密度
通过网格划分将参数空间划分为体积相等的各个网格单元,将每一个网格单元中包含的数据个数作为该网格单元的密度ρ。
2.4 数据压缩比
每一维划分的网格单元个数K 就代表着数据压缩的程度,本文通过定义数据压缩比η来设置参数K:
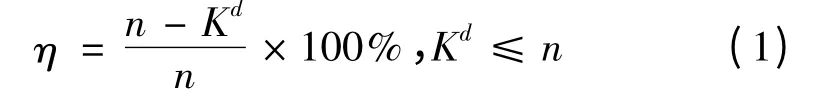
式中,n为待分选脉冲个数,d为特征参数的维数。
K 值越大,对应的数据压缩比越小,划分的网格数越接近数据个数,此时会产生许多空网格耗费存储空间,并且计算代价也将增大;当K 值过小时,会将大量噪声和不同类数据划分到同一网格中去,给聚类精度带来很大的影响。综合两方面的因素,经过大量仿真验证,当数据压缩比取70%时,既可保证分选实时性又能获取较高的聚类精度。
2.5 传统网格聚类算法局限性分析
传统网格聚类中只设定一个密度阈值ε',当网格密度ρ >ε'时,该网格为密集网格,然后将相邻密集网格联通的最大集合作为一类数据;若ρ<ε'时,该网格判为非密集网格,予以舍弃。这种密度阈值的设置是不合理的,会使密度没有达到该阈值的一些真实数据被当作噪声舍弃。通过图2 可以更加清楚地说明这个问题。
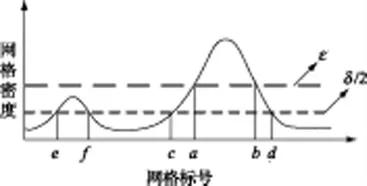
图2 网格聚类密度示意图
图2中c~d 段代表某一类真实数据网格,e~f 段代表噪声分布较密集的网格。假设一个较大的密度阈值ε,则只有a~b 段的网格可以被聚类,而c~a、b~d段以及两段边缘的密度小于ε的网格将被舍弃,这将使一部分数据丢失从而降低聚类精度;假设一个较小的密度阈值δ/2,则某些噪声较为密集的网格(如e~f段)也会被认为是某一类而聚类,产生“增批”现象,并且对于c~d 段两侧边缘的网格依然不能被聚类。针对以上问题,本文设计了双密度阈值策略和边缘稀疏网格优化方法。
3 改进网格聚类算法
3.1 双密度阈值策略
如图2所示,ε 是第一层密度阈值,设置为空间中网格单元的平均密度加上标准差的一半;δ/2 是第二层密度阈值,设置为统计学中判断离散度的标准差的一半。计算过程如下:
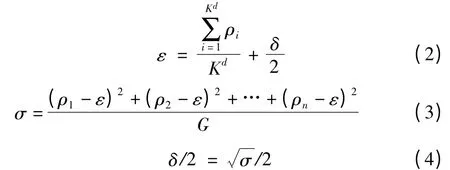
式中,ρi为第i个网格单元的密度,K为每一维划分的区间个数,d 代表参数空间的维数,G为参数空间中非空网格的个数,σ为方差代表数据离散程度。
根据双密度将网格划分为3 种状态:当ρi≥ε时,该网格为密集网格,如图2中a~b 段的网格;当ε >ρi≥δ/2时,该网格为过渡网格,如图2中c~a、b~d、e~f 段的网格;当ρi<δ/2时,该网格为稀疏网格,如图2中除去e~f、c~d 段之外的网格。
在每一次进行聚类时,首先选取未被聚类且密度最大的网格U0,判断该网格是否为密集网格,只有当网格U0是密集网格时,才以网格U0为聚类起始点开始聚类。依据广度优先搜索原则[10]依次访问网格U0的相邻网格单元,并将其中未被聚类的过渡网格和密集网格Ui(i=1,2,3,…,i)都归属到该类,然后再顺序访问所有与网格Ui(i=1,2,3,…,i)相邻的未聚类网格单元,重复上述过程并进行归类,直到所有未聚类的相邻网格单元都是稀疏网格,此时对不为空的边缘稀疏网格进行优化处理。优化处理后,对剩余数据按照上述方法进行下一次聚类,直到选取的U0不是密集网格时该批数据完成聚类。
将聚类起始网格规定为密集网格,可以避免一些噪声分布较为密集的网格被聚类,如图2所示。只能选择a~b 段的密度最大的网格作为聚类起始网格,而不会选择e~f 段的网格作为起始网格,从而避免将一些噪声网格聚类造成“增批”现象,提高了算法的抗干扰能力。
3.2 边缘稀疏网格优化方法
在对某一类数据进行聚类的过程中,当所有未聚类的相邻网格单元都是稀疏网格时,对不为空的边缘稀疏网格进行优化处理。如图3所示,c2、c4 网格为密集网格,c1为过渡网格,其他都为稀疏网格。以稀疏网格b3中的数据点p 进行优化处理举例:首先,计算与网格b3 相邻的非空网格中数据点到点p的欧氏距离;其次,记录每个相邻网格中欧氏距离di≤r(i=1,2,3,…,i,r为归属度门限值,选取为网格边长的最大值)的个数,将该个数作为数据点p 对应该网格的归属度,记为Sn(n=1,2,3,…,n,n为相邻网格标号),图中点p对于邻近非空网格b2,c2,c3,c4,b4,a4,a3的归属度依次为1,1,2,5,1,0,1;最后,比较点p的归属度,选取归属度最大的网格将数据点p 归属到该网格所属的类中去,图中点p 将归属到网格c4所属的类1中去。需要指出的是:当数据点对几个网格的归属度相等时,将同一类的网格归属度累加,计算数据点对类的归属度,然后再比较数据点对不同类的归属度,从而判断该点的归属问题。
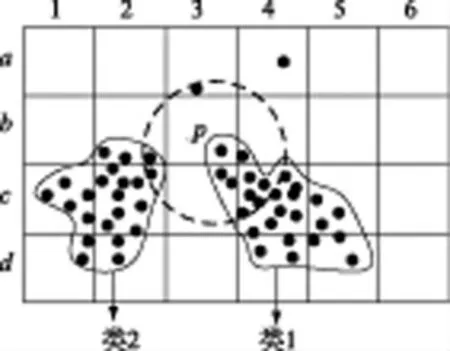
图3 边缘优化示意图
如果应用传统网格聚类算法,只将密集网格c2、c4聚类,将会丢失大量有用数据,严重影响聚类精度。然而,本文提出的边缘优化方法在双阈值策略的基础上对边缘稀疏网格里的数据点依据“类内聚集度”(对比数据点到各个类别的归属度)进行判别归属,可以很好地解决分布在网格边缘数据的归属问题,从而提高聚类精度。
3.3 算法流程
下面结合图4 介绍改进网格密度聚类算法的具体步骤:
(1)对待分选数据集中存储的参数数据进行归一化处理;
(2)依据设定的数据压缩比η来确定K 值的大小,对整个空间进行划分,并将归一化后的数据投影到网格空间中。计算每个网格的密度,对所有非空网格设置状态标签label。在聚类过程中该标签随对应网格状态的变化而变化,label=0 表示该网格未聚类,label=1 表示该网格已聚类;
(3)由每个网格的密度及非空网格的个数依据式(2)、(3)、(4)来计算两个密度阈值;
(4)选取网格中密度最大的网格作为聚类起始点,依据3.1 小节提出的自适应双密度阈值策略进行聚类;
(5)对边缘稀疏网格依据3.2 小节提出的边缘优化方法进行优化处理,优化处理后,标志该类数据聚类完成;
(6)选取剩余未聚类网格中密度最大的,如果该网格是密集网格,则跳至步骤(3),表示还有新的类别;如果不是密集网格,表示该批数据全部完成聚类。
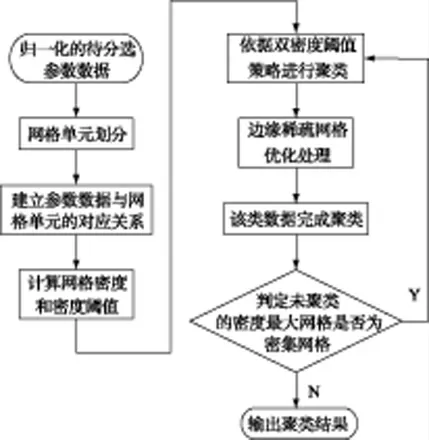
图4 改进网格密度聚类算法流程图
4 仿真实现及结果分析
实验采用的仿真平台为Intel CPU Q8200,3GB 内存,操作系统为Windows XP,仿真软件为Matlab R2010a。利用计算机形成脉冲描述字序列(PDW)来模拟接收机输出的侦察数据流,针对PDW中各个参数的特点和分选要求,实验选择其中最稳定的3个参数PW、RF、DOA 作为特征参数进行聚类。
为了验证改进网格聚类算法应用于雷达信号分选的有效性和对噪声脉冲的识别能力,在脉冲数据中加入了15%的噪声脉冲。实验选用的雷达类型、数目、脉冲个数以及特征参数信息如表1所示,原始信号参数的归一化二维分布如图5所示。
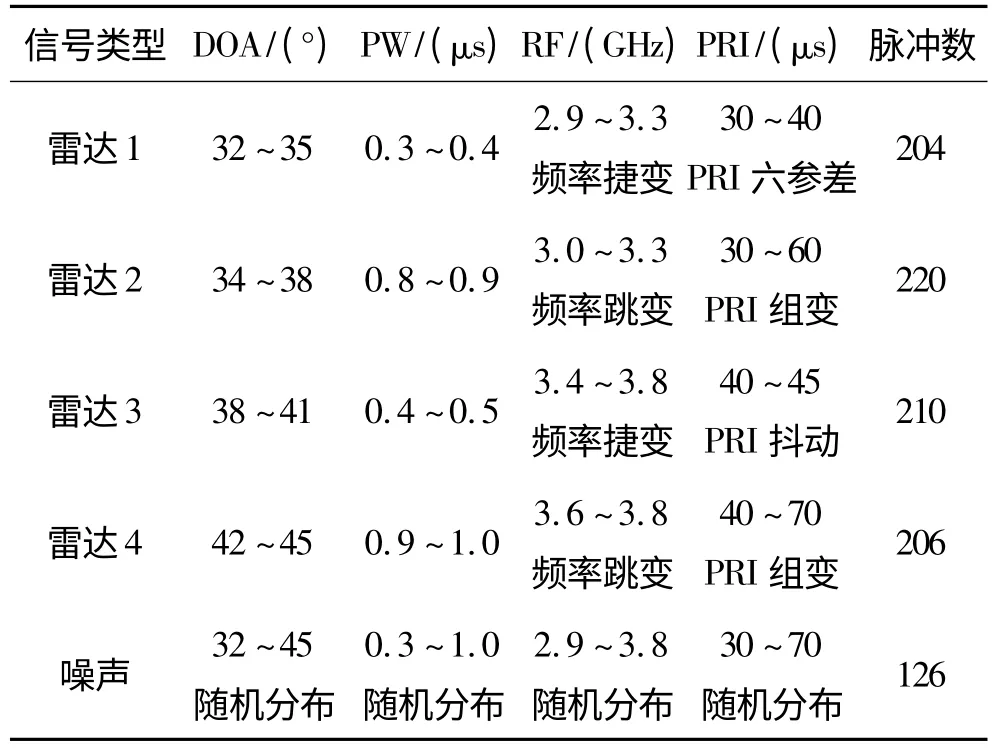
表1 侦察数据信息表
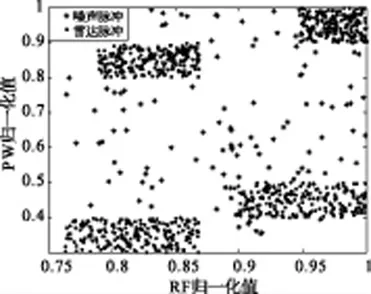
图5 原始信号参数归一化分布图
分别利用传统网格聚类算法和改进网格聚类算法对原始数据进行处理,数据压缩比η=70%,仿真结果如图6所示。
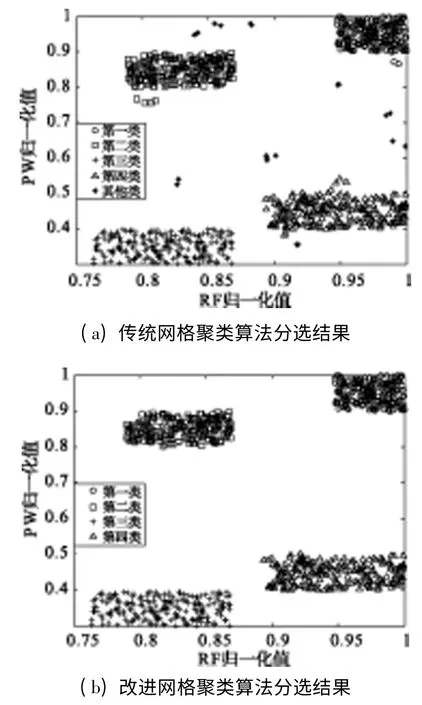
图6 分选结果对比图
由图6(a)可以看出,传统网格聚类算法由于阈值设置为空间中网格单元的平均密度,一些密度累积较大的噪声脉冲将会被当作真实类别而聚类。所以,传统算法受噪声脉冲影响巨大,不仅在真实聚类结果中存在大量的噪声脉冲,而且将噪声脉冲当作真实类别进行聚类,出现了严重的“增批”现象(如图中的符号*代表噪声被算法聚成许多的类)。而图6(b)中改进网格聚类算法使用了双阈值策略,将初始聚类网格的阈值依据数据的离散度进行提高,防止一些密度较大的噪声脉冲被当作真实脉冲而聚类。同时,由于真实类别的网格密度(数据最密集处)要远大于改进后的第一层密度阈值(只要大于第一层密度阈值就可以进行聚类),所以避免了目标丢失的现象。由图可以看出,改进后的算法能够正确地将数据聚成4类,并且受噪声影响较小,去除了大量散落在真实脉冲参数值之外的噪声脉冲,取得了良好的分选效果。具体分选结果如表2、表3所示,其中分选准确率为准确分选的脉冲总数与实际脉冲总数之比。
从表2、表3的统计结果可以看出,传统网格聚类算法虽然用时较少,但误分选和漏分选脉冲数目较多,并且聚类结果中存在9个由噪声组成的类,即出现“增批”现象,对分选结果产生巨大影响。而改进网格聚类算法虽然运算总时间略大于传统算法,但其受噪声脉冲影响较小,不产生“增批”现象,并且聚类精度较传统算法有较大提高。整体而言,改进网格聚类算法对先验知识要求较低,受噪声脉冲的影响较小,分选准确率高,并且具备较高的运算速率,能够有效地完成雷达信号的分选任务。
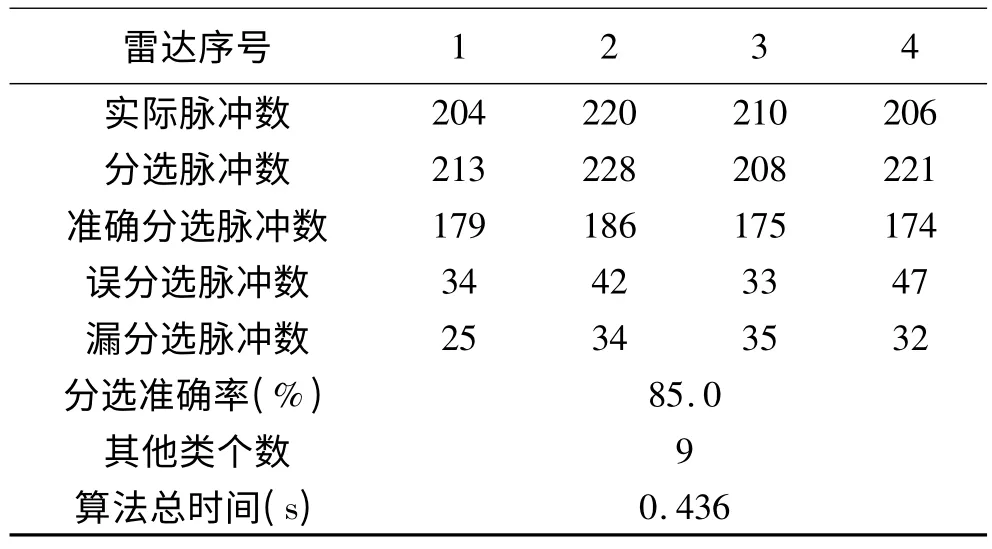
表2 传统网格聚类算法分选结果
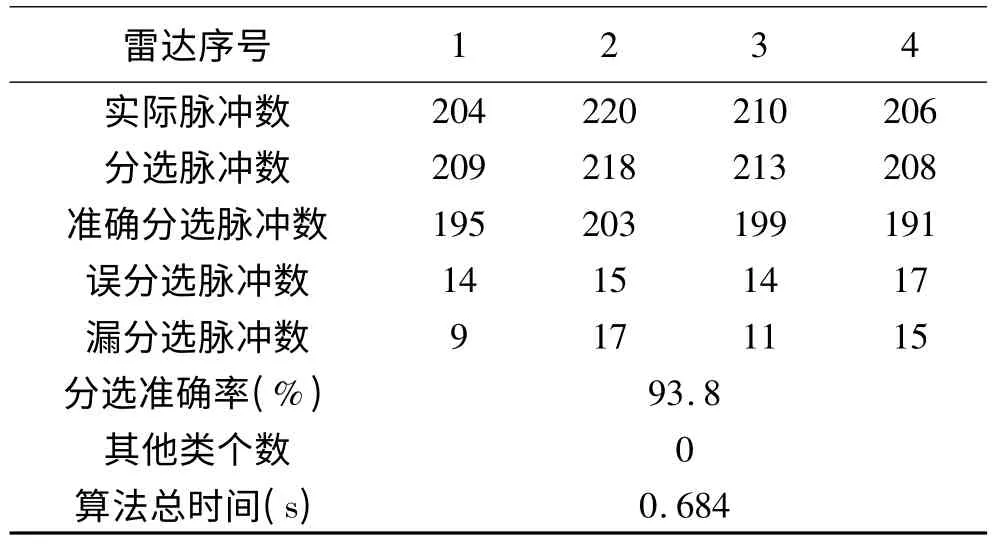
表3 改进网格聚类算法分选结果
5 结束语
本文提出了一种基于改进网格聚类的动态雷达信号动态分选算法,算法将CluStream 数据流聚类经典双层框架引入雷达信号分选中,增加了整个分选系统的实时性。改进了传统网格聚类算法,通过双密度阈值策略使聚类密度阈值更加合理化,增强了抗干扰能力,并且利用边缘稀疏网格优化方法进一步提高了聚类精度。通过仿真验证,证实了该算法较传统算法具备较高的聚类精度和抗干扰能力,适用于现代雷达信号分选系统。
文中提出的方法虽然提高了聚类精度和抗干扰能力,但在噪声信号密集情况下有时仍会出现“增批”现象,如何避免“增批”现象并且进一步提高算法的效率还需要更加深入研究。
[1]Davies C L,Holland P.Automatic Processing for ESM[J].IEE Proc F Commun Radar & Signal Process,1982,4(8):52-56.
[2]Mardia H K.Adaptive Clustering for ESM[J].IEE Colloquium on Signal Processing for ESM systems,1988,62(5):149-154.
[3]Milojevic D J,Popovic B M.Improved Algorithm for the Deinterleaving Radar Pulses[J].IEE Proceedings,Part F:Radar and Signal Processing,1992,139(1):98-104.
[4]胡来招.平面变换用于复杂环境的信号处理[M].电子工业部29 研究所科技成果汇编,1995.
[5]Anant Ram,Ashish Sharma,Anand S Jalall.An Enhanced Density Based Spatial Clustering of Applications with Noise[J].IEEE International Ad-vance Computing Conference,2009 (3 ):1475-1478.
[6]Shan Shimin.Research on data stream clustering based on grid and density[D].Dalian University of Technology,2006.
[7]Aggarwal C C,Han J,Wang J,et al.A Framework Clustering Evolving Data Streams[C]// Proc.of the 29th VLDB Conference,2003:81-92.
[8]张国毅,王晓峰,张旭洲.基于数据流聚类的动态信号分选框架[J].电讯技术,2011,51(9):65-68.
[9]AGGARWAL C C,HAN J,WANG J,et al.A frame work for projected clustering of high dimensional data streams[C]//Proc.of the 30th VLDB Conf,2004:852-863.
[10]张忠平,王爱杰,陈丽萍.一种基于广度优先搜索的K-Means 初始化算法[J].计算机工程与应用,2008,44(27):159-161.
