幂函数荷载作用下图乘法的一种新方法

杨立军, 陆守明, 孙 晋

(1. 湖南文理学院 土木建筑工程学院, 湖南 常德, 415000; 2. 广西大学 土木建筑工程学院, 广西 南宁, 530004)

幂函数荷载作用下图乘法的一种新方法

杨立军1, 2, 陆守明1, 孙 晋1

(1. 湖南文理学院 土木建筑工程学院, 湖南 常德, 415000; 2. 广西大学 土木建筑工程学院, 广西 南宁, 530004)

给出了幂函数荷载作用下求解结构位移的图乘法的一种新方法. 首先介绍了结构在复杂荷载作用下的弯矩图的叠加原理, 然后研究了幂函数分布荷载作用下的弯矩图的面积及形心位置. 求出弯矩图的面积及形心位置后根据叠加原理可以由此求解结构在幂函数荷载作用下的位移. 该方法可以避免采用结构力学传统方法对非标准抛物线图形求解时常见错误, 是对结构力学图乘法的一种有益尝试与探索.

幂函数; 图乘法; 抛物线; 位移计算

在计算梁和刚架的位移和力法方程的自由项和系数时, 常常要计算形如的积分式和MP分别为单位荷载和荷载作用下结构的弯矩图). 为了避免求积分的麻烦, 常常采用图乘法计算该积分式. 一般的结构力学教材给出了几种常见图形的面积公式和形心位置, 以便于图乘法计算. 但存在的问题是, 一是只给出常见的图形, 在有些情况下不能查表计算; 二是教材中在给出抛物线图形时, 有不准确的论述, 在涉及到抛物线图乘时, 极易产生错误[1]. 关于图乘法很多学者做了许多有意义的研究, 为图乘法的发展作出了有益的探索. 如任凤鸣对图乘法简化计算进行了研究[2], 张俊友剖析了图乘法计算结构位移的应用[3],游猛讨论了图乘法和重积分法求纯弯曲梁挠曲线的问题[4], 宋祖民、胡景龙等提出了结构计算位移的新方法： 系数法和牛顿-柯特斯方法[5-6]. 本文则对幂函数荷载作用下的图乘法进行了研究, 给出了幂函数荷载作用下求解结构位移的图乘法的一种新方法.

1 复杂荷载作用下的弯矩图的叠加原理

图1 复杂荷载作用下的弯矩图的叠加

2 幂函数荷载作用下的弯矩图的面积及形心位置

幂函数级数荷载q(x)可以表示为：

由叠加法, 结构在式(1)所示的分布荷载q(x)作用下的弯矩等于结构分别在荷载单独作用下的弯矩MiP的叠加. 同理,和MP的图乘结果就等于和分别图乘, 然后再对之进行代数求和的结果. 现在讨论简支梁在单个幂函数荷载作用下的弯矩图面积及形心位置. 如图2(a)所示的跨度为l的简支梁AB, EI为常数, 承受幂函数荷载. 设梁AB左端支座反力FA, 由右端支座弯矩MB=0, 有：

梁AB任意截面x的弯矩M(x)为：

弯矩图如图2(b)所示. 求出弯矩M(x)的表达式后, 可以求出最大弯矩Mmax的数值及与左端的距离x0.由, 有：

求解式(4), 即可求出Mmax与左端的距离x0为：

图2 幂函数分布荷载作用下的弯矩图的面积及形心位置

将式(5)代入式(4), 求出最大弯矩Mmax为：

如图2(b)所示的弯矩图的面积A为：

由式(3)和式(7), 弯矩图形心到A端的距离x1, 到B端的距离x2为：

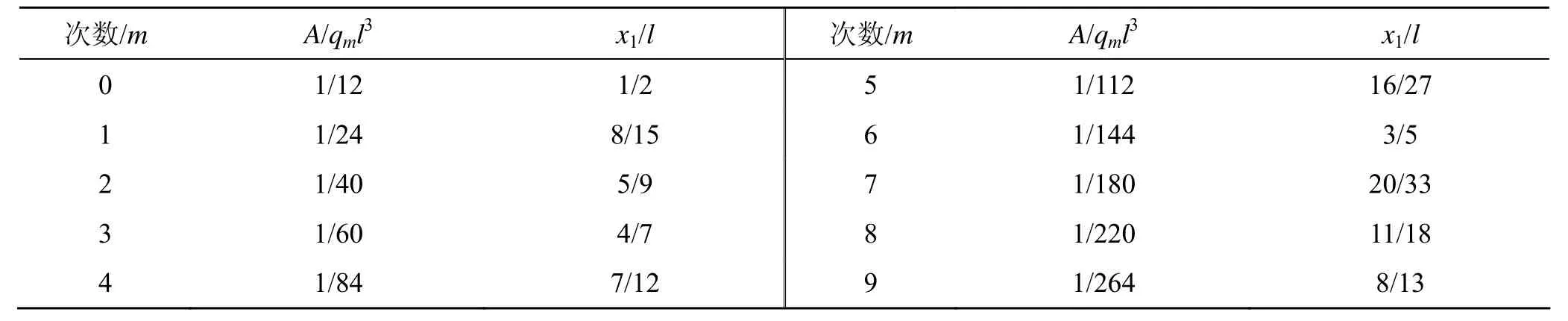
表1 m次幂函数荷载作用下的简支梁AB弯矩图的面积和形心位置

3 算例

算例1如图3(a)所示跨度为l的悬臂梁AB, EI为常数, 全跨承受均布荷载q, B端受有集中力ql, 求B点的竖向位移.

弯矩图如图3(b)所示. 采用本文方法, 将MP图分解为一个三角形和一个抛物线图形, 有：

采用结构力学所给常见图形的面积和形心位置来求解, 有：

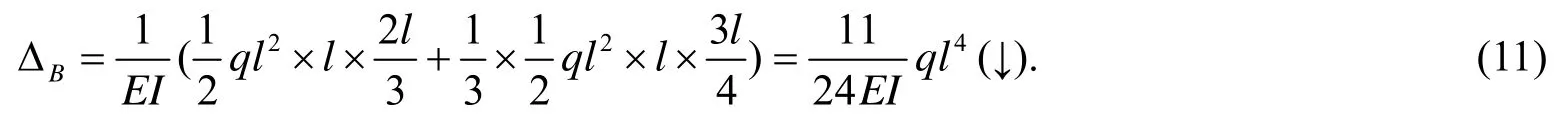
两种方法计算的结果是相同的, 验证了本文方法的正确性.

算例2如图4(a)所示跨度为l的悬臂梁AB, EI为常数, 全跨承受如图所示三角形荷载, 荷载最大值为q0, 求B点的竖向位移.

弯矩图如图4(b)所示. 弯矩图B点处切线与基线平行, 且是顶点, 按《结构力学》教材, 如文献[7], 该图形为三次标准抛物线图形, 则可按《结构力学》教材上三次标准抛物线图形的面积和形心位置来求解, 有：

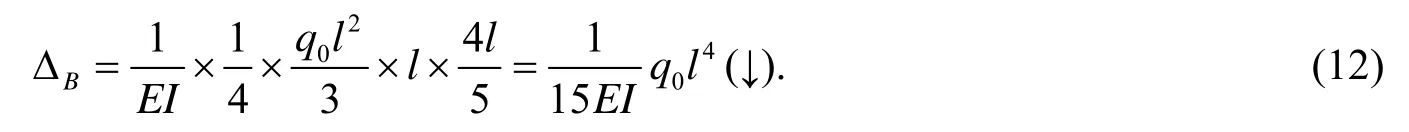
但式(12)计算是错误的. 实际上, 图4(b)所示弯矩图不是标准抛物线图形, 建立如图4(a)所示坐标系, B点为坐标原点, 梁的纵轴线为x轴, 则荷载可以表示为, 梁AB任意截面x的弯矩M(x)为：

M(x)不是齐次的, 故而图4(b)所示弯矩图不是标准抛物线图形. 采用《结构力学》教材所给标准抛物线图形的面积和形心位置, 很容易发生这样的问题.

采用本文所给方法计算, 将MP图分解为一个三角形和一个抛物线图形, 有：

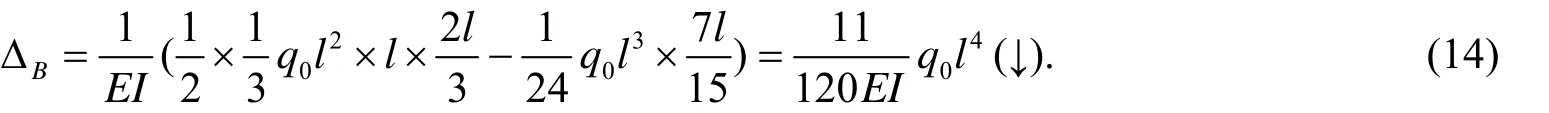
图3 均布荷载和集中荷载作用下的悬臂梁和弯矩

图4 三角形荷载作用下的悬臂梁和弯矩

算例3 如图5所示跨度为l的简支梁AB, EI为常数, 全跨承受如图所示荷载, 求简支梁A端转角.

算例4 如图6(a)所示跨度为l的简支梁AB, EI为常数, 全跨承受如图所示三角形荷载, 荷载最大值为q0, 求梁AB中点C的竖向位移.

MP弯矩图如图6(b)所示. 为求梁AB中点C的竖向位移, 将MP图分成AC和CB两段, 分别与对应的图乘, 然后求和. 将AC和CB两段MP图还原为简支梁的情况, 即： AC段分解为一个三角形(底为0.5l, 高为MP图C点弯矩MC)和三角形荷载(底为0.5l, 高为0.5q0)作用下的三次抛物线, CB段分解为一个三角形(底为0.5l, 高为MP图C点弯矩MC)、均布荷载(0.5q0)及三角形荷载(底为0.5l, 高为0.5q0)作用下的二次、三次抛物线. MP图C点弯矩MC由式(3)求得, 由本文方法, 有：

本题还有简便的方法. 由对称性, 如图6(a)所示中点C的竖向位移和如图7(c)所示中点C的竖向位移相同的. 由叠加法, 如图7(a)所示均布荷载q0作用下的简支梁可以分解为图7(b)和图7(c)的所示简支梁情况的叠加, 即如图6(a)所示三角形荷载作用下的简支梁中点C的竖向位移等于如图7(a)所示均布荷载q0作用下的简支梁中点C的竖向位移的一半, 用本文方法和传统方法均可以求得.

图5 幂函数级数荷载作用下的简支梁

图6 三角形荷载作用下的简支梁和弯矩

图7 三角形荷载作用下的简支梁中点位移等于均布荷载作用下的简支梁中点位移的一半

[1] 陈敏. 图乘法求位移中关于标准抛物线的一种误解[J]. 力学与实践, 1994, 16(1): 63.

[2] 任凤鸣, 汪新, 郭仁俊. 改进力法计算的研究[J]. 力学与实践, 2010, 32(4): 83-86.

[3] 张俊友, 李晓飞, 温艳霞, 等. 图乘法计算结构位移的应用剖析[J]. 内蒙古农业大学学报: 自然科学版, 2008, 29(1): 220-222.

[4] 游猛. 用图乘法和重积分法求纯弯曲梁挠曲线问题的讨论[J]. 力学与实践, 2009, 31(2): 82-83.

[5] 宋祖民, 周利清. 结构计算位移的一种简便方法——系数法[J]. 固体力学学报, 2008, 29(S1): 204-209.

[6] 胡景龙, 李青宁, 阎艳伟. 结构位移计算的牛顿——柯特斯方法[J]. 力学与实践, 2008, 30(2): 93-95.

[7] 李廉锟. 结构力学(上册)[M]. 4版. 北京: 高等教育出版社, 2004: 104.

(责任编校： 刘刚毅)

A new method of diagram multiplication under power function load

YANG Li-jun1, 2, LU Shou-ming1, SUN Jin1
(1. College of Civil and Architecture Engineering, Hunan University of Arts and Science, Changde 415000, China; 2. College of Civil and Architecture Engineering, Guangxi University, Nanning 530004, China)

A new method of diagram multiplication was given that was used for solving structural displacement under power function load. Firstly the superposition principle in bending moment diagram was introduced of structure under complicated load. Then the parameters of bending moment diagram such as area and shape center position, have been calculated when structure under power function load. According to the area and shape center position of bending moment diagram, the structural displacement could be solved by the application of superposition principle under power function load. The method can avoid common errors as non standard parabola with traditional method, and it is a kind of beneficial attempt and exploration in graph multiplication of structural mechanics.

power function; diagram multiplication; parabola; displacement calculation

TU 311

1672-6146(2012)02-0056-04

10.3969/j.issn.1672-6146.2012.02.014

2012-05-28

湖南省“十二五”重点建设学科(机械设计及理论); 湖南省科技计划项目(2010SK3051); 湖南省教育厅科研项目(10C1007)和常德市科技计划项目(2010ZX18)资助.

杨立军(1976-), 男, 副教授, 博士生, 研究方向： 建筑结构振动理论. E-mail： yanglj9601@163.com.