Taub定理的完整证明

杨锦波

(广州大学 物理与电子工程学院, 广东 广州, 510006)

Taub定理的完整证明

杨锦波

(广州大学 物理与电子工程学院, 广东 广州, 510006)

采用Hawking和Ellis证明Birkhoff定理的方法, 完整地证明了Taub定理, 即Einstein方程的平面对称真空解必然为Taub时空.

平面对称真空解; Taub时空; Taub定理

Taub定理由Taub在1951年提出[1-2], 这是一条与广义相对论中著名的Birkhoff定理相类似的定理. Birkhoff定理说: Einstein方程的真空球对称解必为Schwarzchild时空. 而Taub定理则指出: Einstein方程的真空平面对称解必为Taub时空.

最初对Birkhoff定理的证明遗漏了另一种可能性[1-2], 后来Hawking和Ellis在《The Large Scale Structure of Space-Time》一书的附录中给出了包含全部可能性的Birkhoff定理的完整证明[3]. 有趣的是, Taub定理也存在相似的情况: 最初对Taub定理的证明也遗漏了另一种可能性, 因此是一种不全面的或不完整证明. 在本文中, 我们参照文献[3]提出的关于Birkhoff定理证明过程, 给出了Taub定理的一个完整证明. 为了简捷, 本文采用自然单位制, 即c = G = 1.

1 平面对称真空Einstein方程

平面对称时空是这样的一个时空, 其等度规群含有与 2维欧氏群同构的子群, 子群的所有轨道都是2维平面. 平面对称条件把度规形式限制成如下形式:

根据克氏符计算出里奇张量, 并代入Einstein真空场方程, 得:

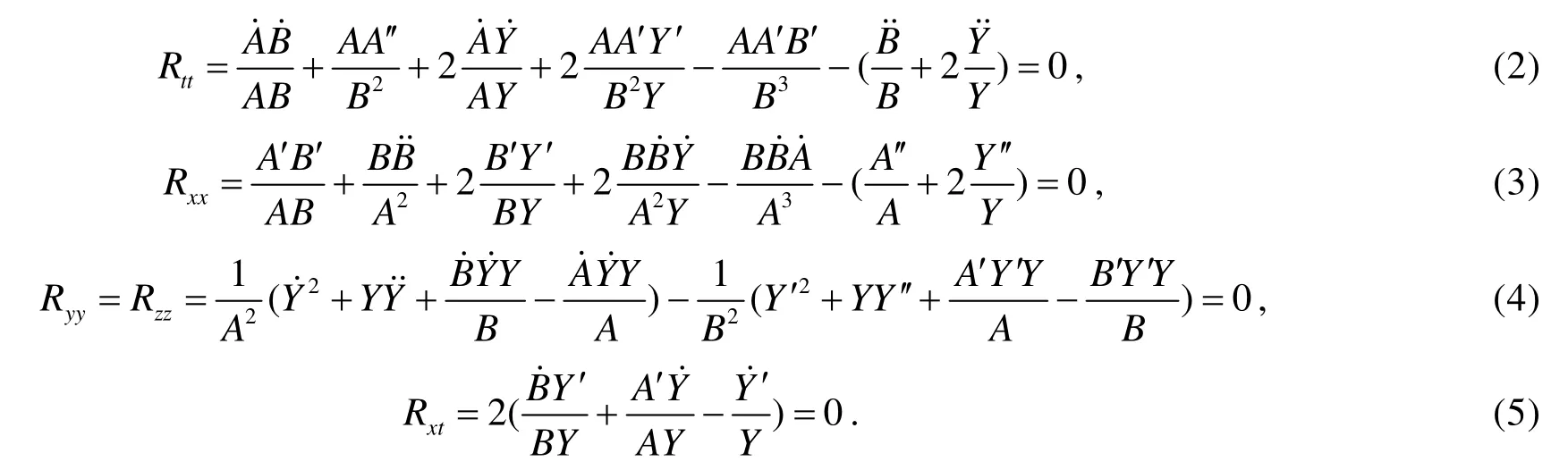
由于广义相对论要求物理规律具有广义坐标变换下的协变性, 这4个方程并不足以确定度规分量的具体的函数形式, 因此本文还将使用谐和坐标条件[2], 即:

仿照Hawking和Ellis在《the large scale structure of Space-Time》的附录B中对Birkhoff定理的证明, 下面将进行分类讨论[3].

2 Taub定理的证明

2.1 Y为常数

当Y为常数时, 我们重新定义y、z, 把系数Y吸收掉, 将线元写为如下形式:

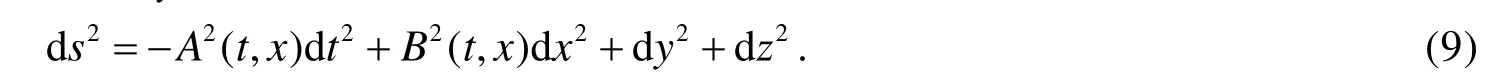
那么Einstein场方程为:

(10)式与(11)式实际上是同一个微分方程:

亦即只有一个独立的方程, 不足以确定度规分量A、B的具体表达式, 这时可以用谐和坐标条件给出的方程(7)和方程(8). 此时, 该两式变为:

由于:

式中γ1和γ2是2个带量纲的常数, 由(14)-(17)式可得:

k是一个待定的常数. 两边取指数, 得:

这意味着可以适当调整k值, 就有A = B, 使度规变成如下形式:

将A = B代入(13)式得:

式中λ为常数. 再对(22)式的两个等式分别积分得:

再积分一次, 得:

最后, 得:

线元的表达式为:

得出的线元表达式看似复杂, 其实正是Minkowski时空, 这只需要通过几步坐标变换就能看出.

做坐标变换w=t-x, v=t+x, 则线元的表达式变为:

则线元就变为:

这意味着, 若Y取常数, 则Einstein真空场方程的解必为Minkowski 时空.

2.2 Y为变量

如果(1)式中的Y是t和x的函数, 那么可以另选坐标系, 使Y是其中的一个坐标:

由(34)、(35)式可得:

用X, Y, y, z作为新坐标, 线元的表达式(1)变为:

则线元可以进一步写为:

也就是可以选取Y作为空间坐标.

则线元可写成:

也就是可以选取Y作为时间坐标.

4) 如果(1)式中的Y仅为t (或x)的函数, 可以由t=t( Y)(或x=x( Y))给出, 线元可写为:

综上所述, 当Y为变量时, 总可以取为时间或是空间坐标.

2.3 取Y = x

取Y = x, 线元变为:

Einstein场方程剩下两个独立的方程：

对(52)式积分得:

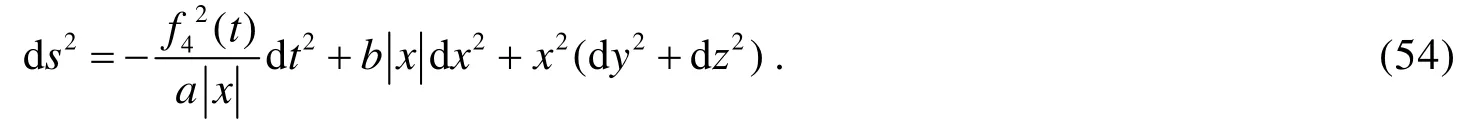
这里不使用谐和坐标条件. 因为在本坐标之下, 谐和坐标条件给出的方程

将给出矛盾的结果, 因此不应该再使用谐和坐标条件.

(58)式与(60)式有相同的形式, 所以只需要讨论(58)式.

重新定义各个坐标量, 把多余的常数吸收掉之后有:

2.4 取Y = t

取Y = t, 线元变为:

场方程变为:

对(64)式直接积分得:

其中a是正实数(与2.3节无关, 下同). 用分离变量法解(65)式, 令, 有:

将A的表达式代入(63)式得:

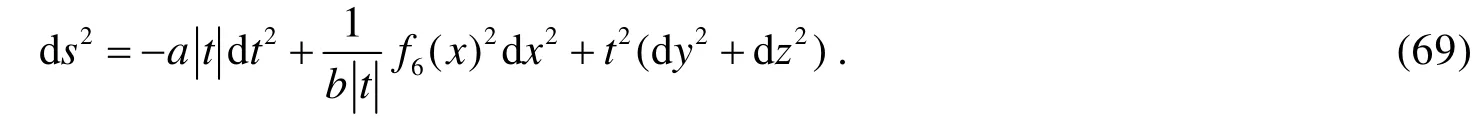
而谐和坐标条件给出:

(71)式与(64)、(65)式矛盾, 与2.3节一样, 应该放弃谐和坐标条件.

当t＜0时,

类似于2.3节, 只需要研究(73)式.

重新定义坐标把不必要的常数吸收掉, 可得:

3 结论

综上所述, 在平面对称的条件下, 真空Einstein场方程的解是:

Taub得到的结果与上述表达式是不一样的, 其结果为:

遗漏的情况是[2]:

文献[2]指出, (81)、(82)式中的k会让人误以为是任意常数, 但是在 k≠0的时候, (81)式经过合适的坐标变换会变成如下形式:

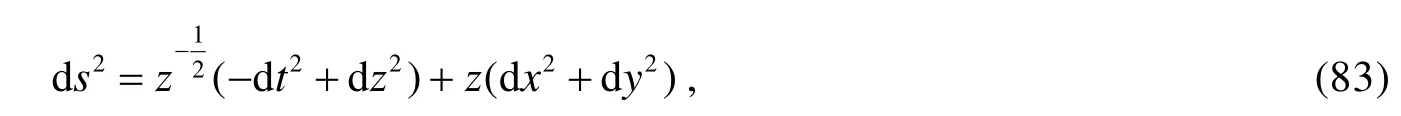
而(82)式会变成[2]:

显然 k=0时, (81)、(83)式都是常用的Minkowski时空线元. 把t, x, y, z的次序交换后就可以把(83)、(84)式变成(79)、(80)式, 可见(78)-(80)式确实是Taub时空所用的线元.

致谢:在本文的撰写过程中, 科普作家张轩中提供了一些相关资料, 并做了一些有益的讨论, 广州大学天体物理中心张靖仪教授提出了一些具体的修改意见, 在此向他们一并致以诚挚的谢意!

[1] Taub A H. Empty Space-time admitting a three parameter group of motion [J]. Ann Math., 1951, 53(3): 472-490.

[2] 梁灿彬. 微分几何及广义相对论(上册)[M]. 2版. 北京: 科学出版社, 2006: 267-270.

[3] Hawking S W, Ellis G F R. The Large Scale Structure of Space-Time[M]. Cambridge, UK: Cambridge University Press, 1973: 369-372.

(责任编校： 江 河)

A complete proof of the Taub's theorem

YANG Jin-bo
(School of Physics and Electronic Engineering, Guangzhou University, Guangzhou 510006, China)

By the same method as Hawking and Ellis proving the Birkhoof's theorem, a complete proof of the Taub's theorem is given. According to the Taub’s theorem, a plane-symmetric vacuum solution of the Einstein equations must be a Taub space-time.

plane-symmetry vacuum solution; Taub space-time; Taub's theorem

O 412.1

1672-6146(2012)02-0021-07

10.3969/j.issn.1672-6146.2012.02.006

2012-3-27

杨锦波(1991-), 男, 本科. 主要研究方向为黑洞物理. E-mail: base.city@163.com