基于时间序列的南昌房地产价格指数模型研究
2012-06-07殷霄雯
殷霄雯
(华东交通大学 国际学院, 江西 南昌, 330013)
基于时间序列的南昌房地产价格指数模型研究
殷霄雯
(华东交通大学 国际学院, 江西 南昌, 330013)
鉴于房地产全国价格指数与实际城市房地产价格相差较大, 本文基于自回归积分移动平均模型理论, 构造了南昌市1998~2011年共55个季度房地产价格指数数据的理论模型ARIMA(3,2,0), 经Box-Pierce检验表明该模型具有95%的概率合理性, 为预测南昌市未来房地产价格指数提供参考.
房地产价格指数; ARIMA模型; Box-Pierce检验
房地产是国民经济重要支柱, 同时住房也是关系百姓的民生大事, 其价格出现变动往往引起社会其他领域深层次的影响. 我国对房地产价格的监控是从1998年实行住房商品化后建立的, 并以房地产价格指数REPI(Real Estate Price Indices的形式向外公布. 外资[1]、利率政策[2]、货币政策[3]、信贷规模[4]、地区差异[5]、收入分配差距[6]对 REPI变化都有贡献, 和其他各种未知社会因素一起引起房地产经济复杂的非线性变化.构造包含每种非线性影响因素的 REPI模型是不易实现的, 时间序列理论只构造指数之间的变化关系, 比较适合对REPI建模. 韦智芳[7]选取美国供应管理协会制造业指数和美国未决房屋销售月率数据, 基于时间序列理论建立了美国经济模型, 并进行了预测; 孙淑珍[8]基于1998年1季度至2008年4季度我国REPI指数, 建立了ARIMA(3,1,0)模型; 姜茜娅[9]建立我国REPI指数的时间序列模型, 通过向后预测与实际吻合较好. 由于REPI指数统计方法的缺陷, 造成理论模型的预测与实际城市房屋价格变动相差较大; 若对实际城市构造理论模型, 则误差大大减小.
本文基于南昌市1998~2011年REPI指数数据, 基于时间序列自回归积分移动平均模型基本理论编制MATLAB程序, 分析了南昌房地产销售价格化趋势, 建立了南昌REPI指数ARIMA(3, 2, 0)理论模型, 为同类型城市REPI指数分析提供参考.
1 自回归积分移动平均模型
如果一个非平稳时间序列{xt}经过 d次差分运算后, 可以生成一个平稳时间序列, 且可以建立如式(1)的模型, 则称{xt}为(p, d, q) 阶的自回归积分移动平均(Autoregressive Integrated Moving Average)序列

式中: φ(L)为平稳的自回归滞后算子多项式,θ(L)为可逆的移动平均滞后算子多项式, (1-L)d为d次差分算子.自回归积分移动平均模型ARIMA(p, d, q)可通过参数变换可以得到自回归移动平均模型ARMA(p,q)、自回归模型AR(p)、移动平均模型MA(q)和白噪声模型, 通过对其自相关函数ACF(Auto Correlation Function)、偏自相关函数(Partial Autocorrelation Function)分析和赤池信息准则进行定阶比较方便, 因而获得了广泛的应用.
2 南昌房地产价格指数模型的建立
2.1 二阶差分后零均值化和平稳性检验
选取南昌市1998年至2011年共55个季度房地产价格指数[11]进行分析. 由于我国房地产价格指数是以上期数据为基准的同比数据, 需转换为以1997年第4季度为基准的指数, 构造成时间序列{xt}图像如图1所示.

图1 南昌市历年房地产价格指数图
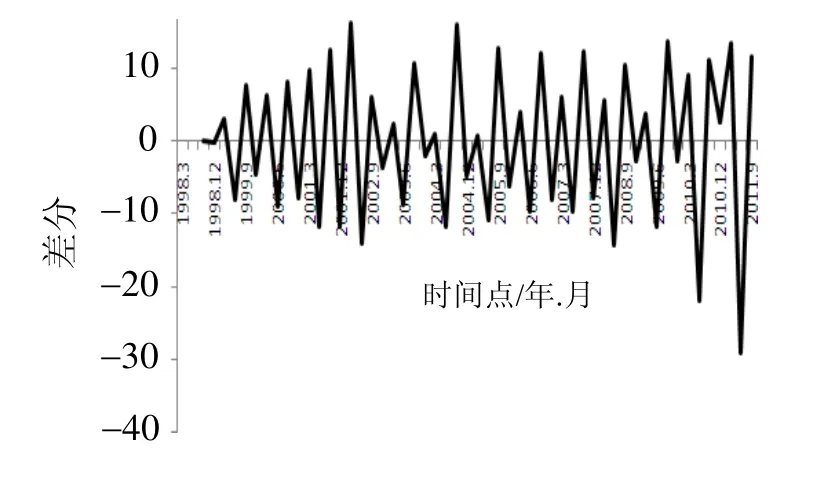
图2 南昌市历年REPI指数二阶差分图
由图 1可以看出南昌市房地产价格指数序列{xt}具有明显的趋势性, 不具备平稳性特点. 对其进行二阶差分后的时间序列如图 2所示, 样本均值为 0.019 9. 将其零均值化得到新的时间序列{yt}, 其均值为1.005 5×10-16, 满足零均值, 它是平稳时间序列的一个条件. 时间序列{yt}的逆序总数为:

式中: Ai为时间序列yi的逆序个数, T为时间序列{yt}的样本容量T=55. 那么有以下统计量关系成立.

式(4)表明时间序列{yt}无趋势成立, 与零均值条件一起表明{yt}是平稳时间序列.
2.2 模型识别与定阶
对{yt}进行自相关ACF与偏相关PACF运算, 其函数图像如图3-4所示.

图3 {yt}ACF函数图像

图4 {yt}PACF函数图像
由图3-4可以看出, {yt}的自相关函数ACF图像具有拖尾性质, 偏相关函数PACF图像具有截尾性质,可以判断该序列属于AR序列. 由图4可以看出, PACF图像当k>3时满足, 可判断模型阶数为3.
2.3 参数估计与模型检验
使用最小二乘法(Least-squares Method)和协方差法(Covariance Method)估计{yt}的参数, 得到了相同的结果.
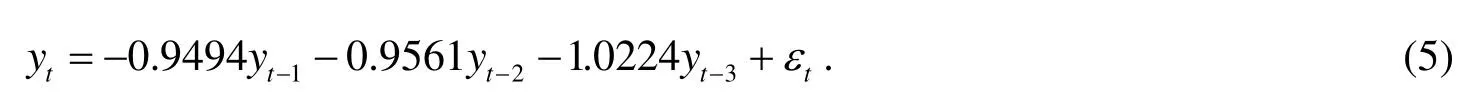
为检验模型与样本的残差是白噪声, 建立残差序列:

2.4 差分模型表达式
根据前述分析, 可以得知南昌市房地产价格指数满足ARIMA(3,2,0)模型型式的条件, 且可表示为:
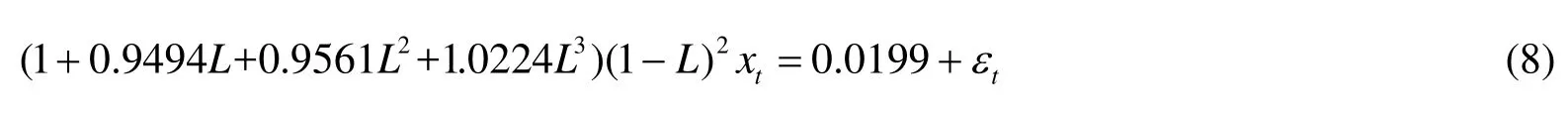
3 结论
本文基于时间序列理论, 分析了南昌市房地产价格指数时间序列模型, 将其表达为ARIMA(3, 2, 0)模型形式, 为预测未来南昌市房地产价格指数水平提供参考.
[1] 陈杰, 郑天. 我国房地产市场发展中的外资因素分析: 我国房地产价格波动与外资影响[J]. 价格理论与实践, 2009(3): 36-37.
[2] 郭娜, 翟光宇. 中国利率政策与房地产价格的互动关系研究[J]. 经济评论, 2011(3): 43-50.
[3] 胡军燕, 陈智辉. 货币政策对房地产价格的动态影响分析[J]. 商业时代, 2011(2): 56-57.
[4] 何静, 李村璞, 邱长溶. 信贷规模与房地产价格的非线性动态关系研究[J]. 经济评论, 2011(2): 21-28.
[5] 孙巍, 朱嫒玲, 王怡. 房地产价格地区差异影响因素的计量分析[J]. 税务与经济, 2011, 177(4): 1-7.
[6] 梁斌. 收入分配差距对房地产价格的影响研究:基于异质性DSGE模型的模拟分析[J]. 金融与经济, 2011, 6: 40-44.
[7] 韦智芳. 时间序列分析法在美国经济预测的应用研究[J]. 现代商业, 2010, 2: 192-194.
[8] 孙淑珍, 刘双. ARIMA模型在房屋销售价格指数预测中的应用及SAS实现[J]. 湖南文理学院学报: 自然科学版, 2010, 22(2): 1-4.
[9] 姜茜娅. 基于时间序列的中国房地产价格走势预测[J]. 知识经济, 2010, 6: 48-49.
[10] 张世英, 樊智. 协整理论与波动模型[M]. 北京: 清华大学出版社, 2009: 1-32.
[11] 中华人民共和国国家统计局. 七十个大中城市房地产价格指数. 中国经济景气月报[J]. 2011(11): 174-175.
[12] 孙荣恒. 应用数理统计[M]. 北京: 科学出版社, 2005: 245-246.
(责任编校: 刘刚毅)
Nanchang city REPI research based on ARIMA model theory
YIN Xiao-wen
(International School, East China Jiaotong University, Nanchang 330013, China)
Because of the error between whole country REPI (Real Estate Price Indices) theoretical model and actual city estate price, Nanchang City REPI theoretical model ARIMA(3,2,0) was established range from 2008 to 2011 REPI data based on ARIMA (Autoregressive Integrated Moving Average) model theory, it was proved to 95% probability acceptable by Box-Pierce test. It may be some referenced use to forecasting future Nanchang REPI.
Real Estate Price Indices; ARIMA model; Box-Pierce test
F 212.1
1672-6146(2012)02-0006-03
10.3969/j.issn.1672-6146.2012.02.003
2012-04-17
江西省教育厅科研基金(JJ1207); 华东交通大学校立科研基金(10QT03).
殷霄雯(1983-), 女, 硕士, 从事宏观及微观经济学的研究与教学. E-mail: yinxiaowen1102@gmail.com
