三体船兴波问题的数值计算
2012-06-07周利兰
周利兰 , 高 高 , 尹 巍
(武汉理工大学 a.交通学院;b.高速船舶工程教育部重点实验室,武汉430063)
1 引 言
近年来三体船的研究渐趋活跃。三体船的水下部分由主体和两个小侧体组成,通过连接桥将侧体与主体连接成一体,这种船型构造使三体船的兴波阻力小,两个侧体又能提供足够的稳性,连接桥具有提高总纵强度的功能,利于形成宽阔甲板面,该船型还具有优良的耐波性。三体船用作军船还有防护能力、破损稳性以及隐蔽性好等优点。尽管高速三体船与常规单体船相比也有制造工艺复杂、制造成本高的缺点,但性能方面的诸多优势使其应用前景广阔。
三体船除单个片体自身首尾波系之间的兴波干扰外,其主体和两个侧体之间的波系干扰导致复杂的兴波波形,因而其阻力特性比单体船的要复杂得多。Zafer Elcin[1]采三维Rankine源面元法系统地研究了侧体位置对三体船兴波阻力的影响。Yang[2]等分别采用包括新细长体理论在内的三种线性理论方法进行三体船侧体位置的优化分析。陈京普等[3]采用改进的Dowson方法,开发了可用于双体船、三体船兴波阻力的数值预报程序。近年发展的船舶兴波问题的基于NURBS的广义高阶面元法算法,对排水型单体船和双体船的计算都获得了成功[4],本文讨论将其应用于三体船兴波问题计算。
2 基本方程与边界条件
在势流假定下,扰动速度势φ满足Laplace方程:

物面边界条件:

自由表面运动学边界条件:

自由表面动力学边界条件:

无穷远条件:

再加上辐射条件即构成定解问题。实际计算中自由表面边界条件采用(3)式与(4)式的耦合条件:
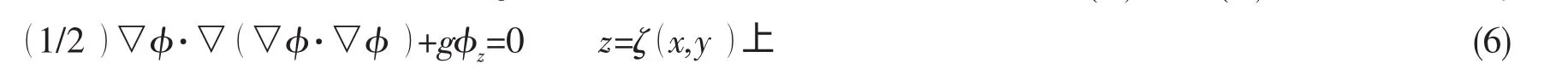
3 数值方法
以Rankine源为Green函数的势流解法由于其函数形式简单且因此易于推广应用于非线性计算问题,所以从它问世到现在的二十多年间一直都是船舶兴波势流计算的主流方法。船舶流体力学问题数值计算中基于NURBS高阶面元法的引入,起到了计算流体力学CFD与船舶工程CAD之间的桥梁作用。
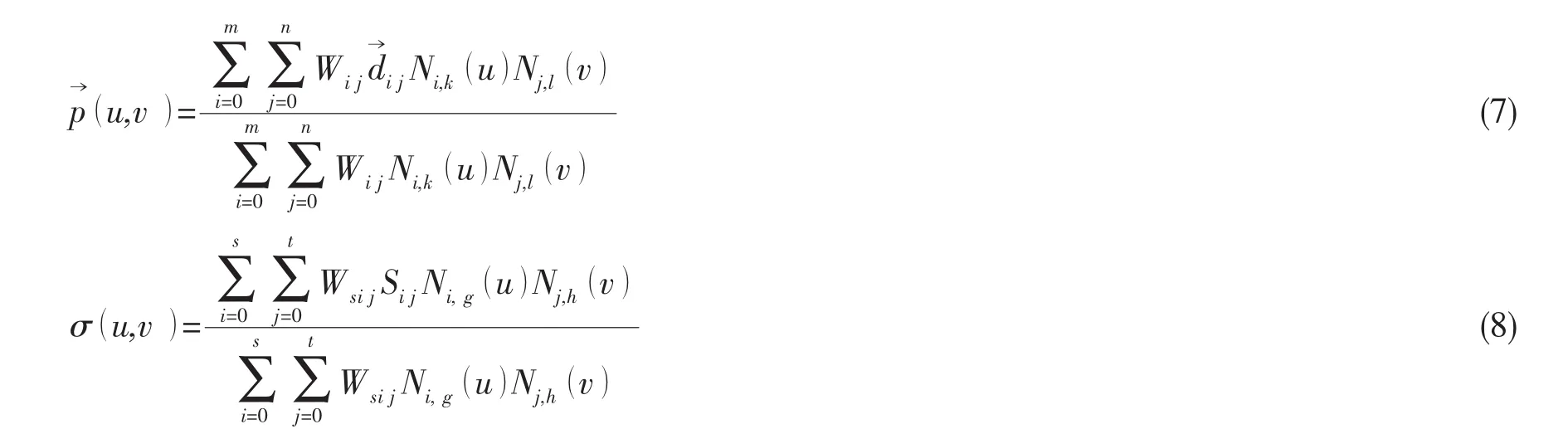

与通常边界元法不同的是,在以上述速度势表达式通过边界条件构造的求解方程组中,直接的变量不是源强密度而是源强分布曲面的控制顶点,在边界面上选取的配置点数目应与源强控制顶点数目相同。
辐射条件的满足是以Rankine源为奇点的面元方法的主要困难之一。本文采用自由面上置源,从而可方便地以配置点移动法数值上满足辐射条件。高高曾分析过有关数值误差,相应参数的取值可参见有关文献[5]。纵向采用均匀网格,配置点前移可由自由面上的源分布曲面后移来实现。最后,自由面上的源分布曲面表为:

式中的δx和zs分别代表自由面上的源分布面沿纵向及垂向的偏移量。此处δx取纵向网格间距,zs取纵向网格间距的1.5倍。
约定以上标F表示相应物理量为自由面上的,上标B表示物面上的,记源点的参数坐标为(u0,v0),则源分布对计算域内任一点(u,v)产生的诱导速度为:
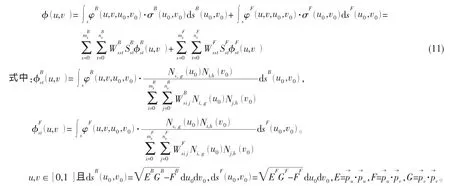
将以上速度势的表达式代入物面边界条件、自由表面边界条件后,即构成了以曲面控制顶点及为未知数的代数方程组,未知数的总数为由于NURBS曲面积分难以解析进行,文中采用分片高斯积分。解得及后,由(9)式决定速度势,进而求得波高及兴波阻力。
4 数值求解与结果
本文数值计算采用两种船型,一种是文献[6]所使用的数学船型;另一种采用文献[7]给出的方尾船型及布局,侧体的尺度比主体的小很多,主体、侧体主尺度要素见下表1。计算域取主体船前0.5水线长,主体船后1.5水线长,主体船侧1.0水线长,主体和侧体均取21×6个配置点,自由面取61×20个配置点。对于三体船,侧体流场的不对称性会对兴波计算带来不同程度的影响,对于船型一,注意到比较的参考文献[6]未计及此影响,本文亦在未计及该影响的条件下进行计算比较;而对于方尾船型二,由于本文在方尾处满足以下方尾边界条件[7]:

该条件等价于以下流动在方尾下缘切向光滑脱体的条件[8](从某种意义上类似于无界域问题中的Kutta条件):
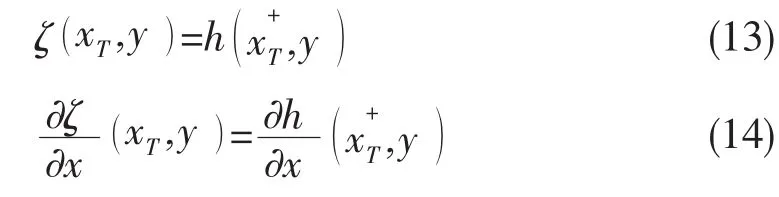
式中:ζ为波高;h为方尾边沿高度;xT,y为方尾处纵、横向坐标;x+T的上标“+”,表示从x的正向(自由面上)趋近于xT(在自由面上)。
为表达三体船侧体布置,记:主体船中至侧体船中的纵向间距为Xs(侧体在主体中前为正),主体船中至侧体船中的横向间距为Ys,如图1所示。
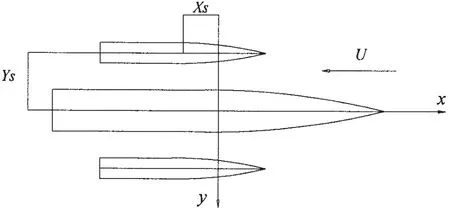
图1 三体船侧体与主体位置关系Fig.1 Configuration of trimaran
文献[6]主体和侧体均采用如下的数学船型:

文中主体船长、船宽及吃水均三倍于侧体。计算取Xs为-1/3L,Ys为0.2L,图2给出了兴波阻力系数随Fn数的变化曲线,图3给出了Xs=-1/3L,Ys=0.2L,Fn=0.5下的三维波形图。计算所得兴波阻力系数与试验结果符合较好,优于文献[6]的计算结果。

表1 三体船主体和侧体主要要素Tab.1 Main dimensions of trimaran
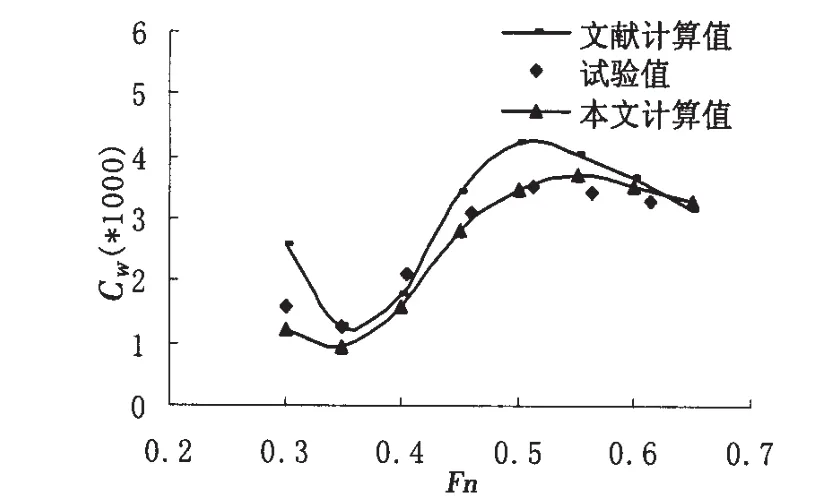
图 2 计算 Cw与文献 Cw之比较(Xs=-1/3L,Ys=0.2L)Fig.2 Calculated wave-making resistance coefficient Cwand referenced Cw(Xs=-1/3L,Ys=0.2L)
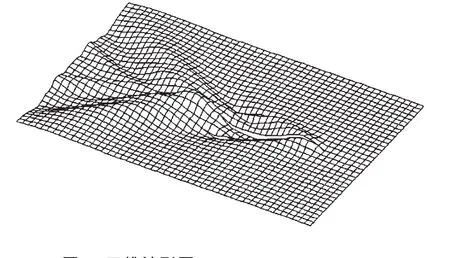
图 3 三维波形图(Xs=-1/3L,Ys=0.2L,Fn=0.5)Fig.3 Three dimensional wave pattern of trimaran(Xs=-1/3L,Ys=0.2L,Fn=0.5)
对于船型二,选取不同的侧体布置参数Xs、Ys,由Xs、Ys组合成不同的侧体布置方案,本文数值计算中分别取 Xs为-0.3L,-0.2L、0L 和-0.1L,Ys为 0.086 5L、0.092 3L、0.105 8L 和 0.111 7L。 图 4-9分别反映了Xs为-0.3L,-0.2L和-0.1L,Ys为0.092 3L和0.111 7L这6种情况下的兴波阻力系数随Fn数的变化,并与模型试验结果得到的剩余阻力系数进行了比较(此剩余阻力系数含有主体、侧体的粘性干扰影响)[9],图10、图11给出了不同横向偏距和纵向偏距共8种情况下兴波阻力预报曲线,图12给出了Xs=-0.3L、Ys=0.073 1的三体船阻力系数图,图13、图14分别Xs=-0.2L,Ys=9 m(0.086 5L),Fn=0.6的船舶兴波的三维波形图和波形等高线图。注意到模型试验结果得到的剩余阻力系数除含有粘压阻力、曲率对摩擦阻力的影响,主体、侧体的兴波干扰影响外,还包含主体、侧体的粘性干扰影响及本文兴波计算采用的是线性自由面边界条件等因素,与模型试验得到的剩余阻力系数相比,计算兴波阻力系数随Fn数的变化合理。计算结果表明:纵向偏距Xs对三体船Cw有显著影响,高速时横向偏距也对Cw有较大影响,这与其他学者对高速三体船侧体的横向偏距和纵向偏距对高速三体船兴波阻力影响规律的研究结果基本一致[10-11];图12中与文献[12]的兴波阻力系数计算结果及试验所得剩余阻力系数的比较,结果表明本文计算结果较优于文献[12]的计算结果。
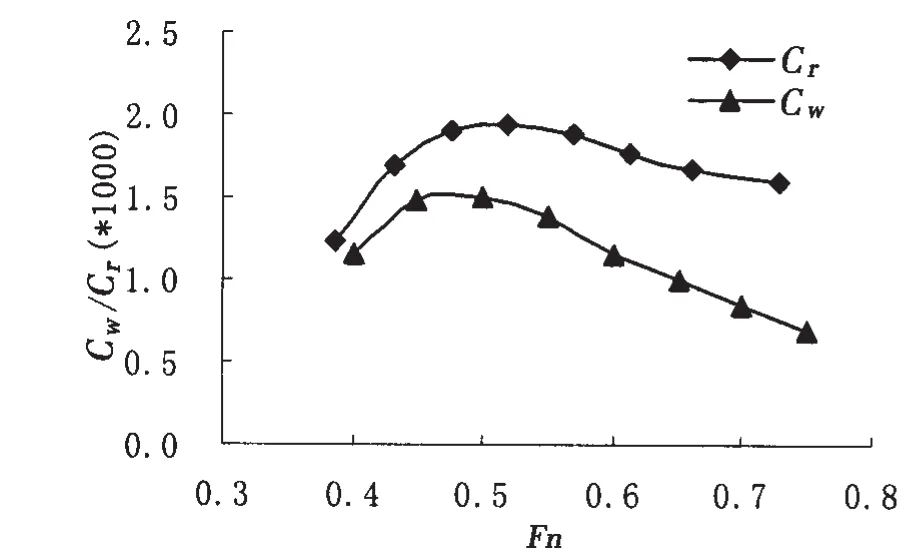
图4 计算的兴波阻力系数Cwp与实验Cr之比较(Xs=-0.1L,Ys=0.092 3L)Fig.4 Calculated wave-making resistance coefficient Cwp and experimental residual resistance coefficient Cr(Xs=-0.1L,Ys=0.092 3L)
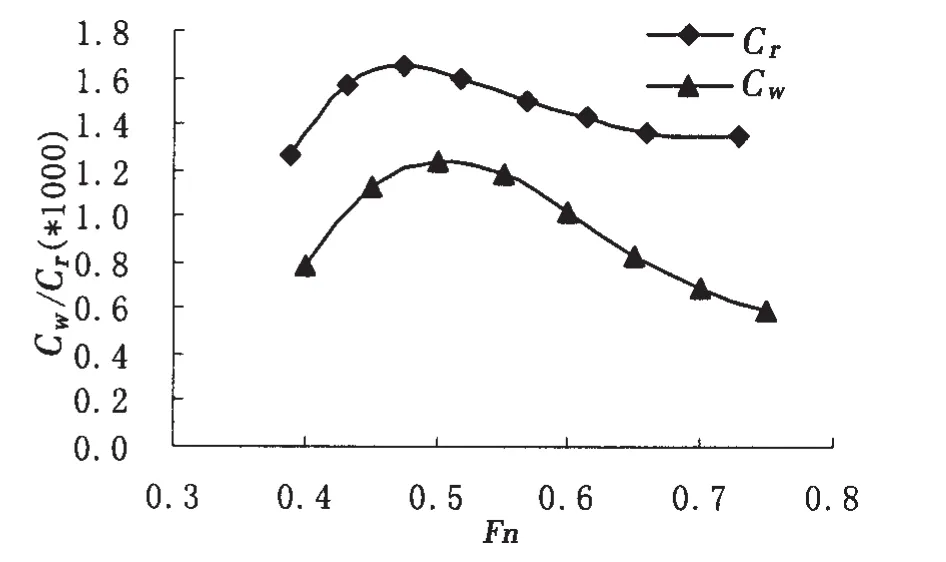
图5 计算的兴波阻力系数Cwp与实验Cr之比较(Xs=-0.2L,Ys=0.092 3L)Fig.5 Calculated wave-making resistance coefficient Cwp and experimental residual resistance coefficient Cr(Xs=-0.2L,Ys=0.092 3L)
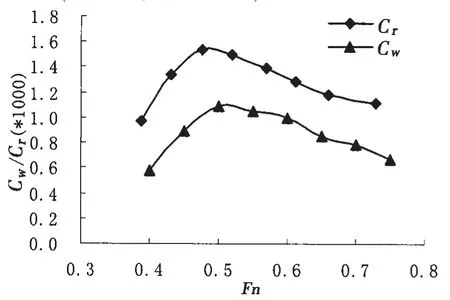
图6 计算的兴波阻力系数Cwp与实验Cr之比较(Xs=-0.3L,Ys=0.092 3L)Fig.6 Calculated wave-making resistance coefficient Cwp and experimental residual resistance coefficient Cr(Xs=-0.3L,Ys=0.092 3L)
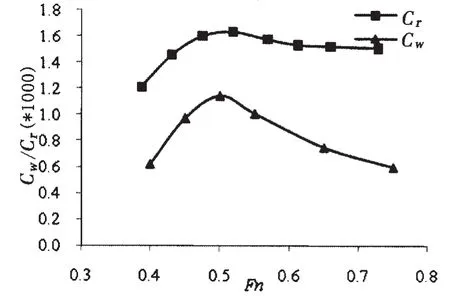
图8 计算的兴波阻力系数Cwp与实验Cr之比较(Xs=-0.2L,Ys=0.111 7L)Fig.8 Calculated wave-making resistance coefficient Cwp and experimental residual resistance coefficient Cr(Xs=-0.2L,Ys=0.111 7L)
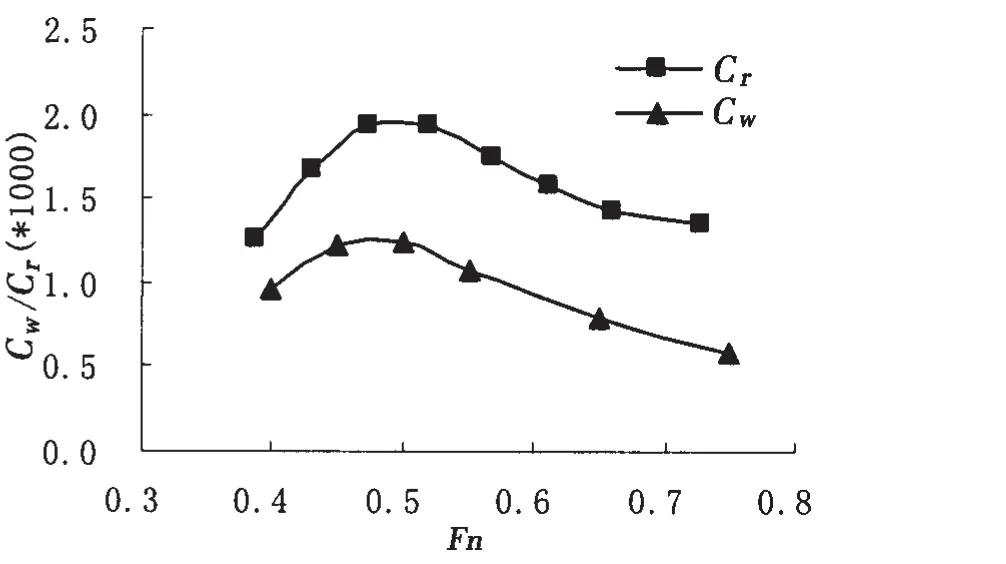
图7 计算的兴波阻力系数Cwp与实验Cr之比较(Xs=-0.1L,Ys=0.111 7L)Fig.7 Calculated wave-making resistance coefficient Cwp and experimental residual resistance coefficient Cr(Xs=-0.1L,Ys=0.111 7L)
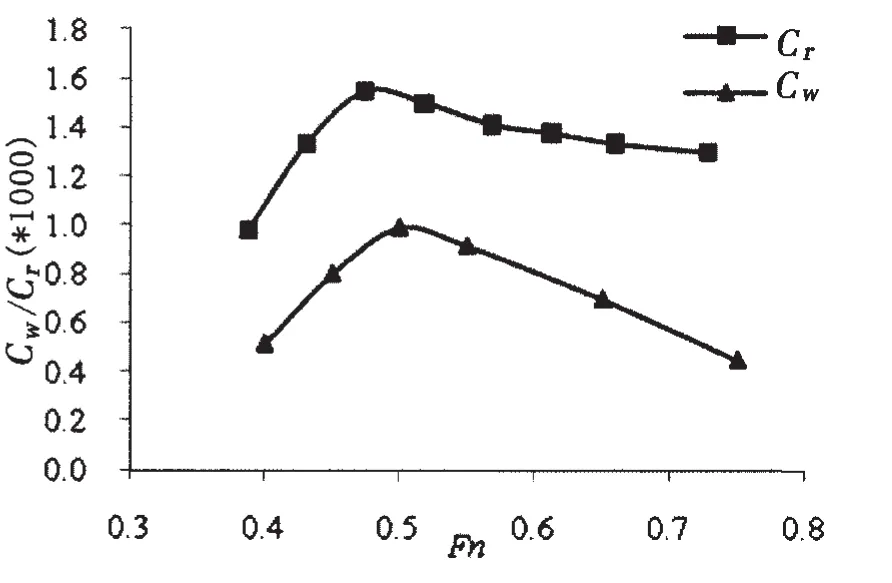
图9 计算的兴波阻力系数Cwp与实验Cr之比较(Xs=-0.3L,Ys=0.111 7L)Fig.9 Calculated wave-making resistance coefficient Cwp and experimental residual resistance coefficient Cr(Xs=-0.3L,Ys=0.111 7L)
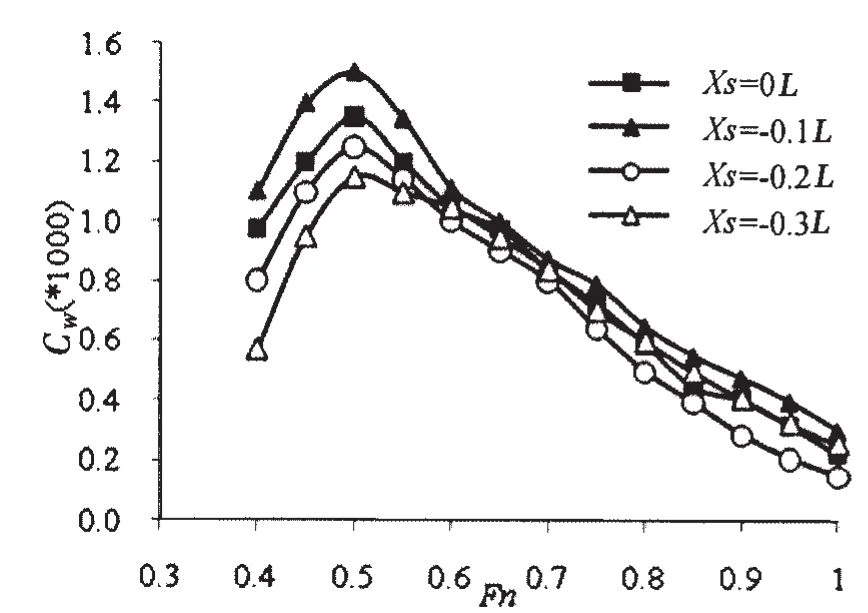
图10 Ys=9 m兴波阻力预报曲线Fig.10 Calculated wave-making resistance coefficient curves for Ys=9 m
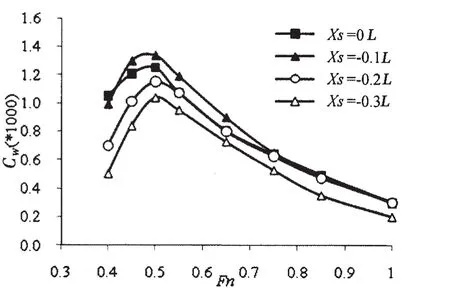
图11 Ys=11 m兴波阻力预报曲线Fig.11 Calculated wave-making resistance coefficient curves for Ys=11 m
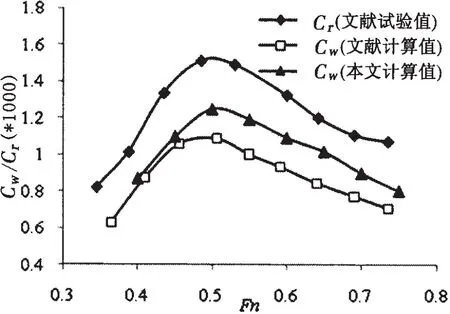
图12 三体船阻力系数比较(Xs=-0.3L,Ys=0.073 1L)Fig.12 Resistance coefficients of trimaran(Xs=-0.3L,Ys=0.073 1L)
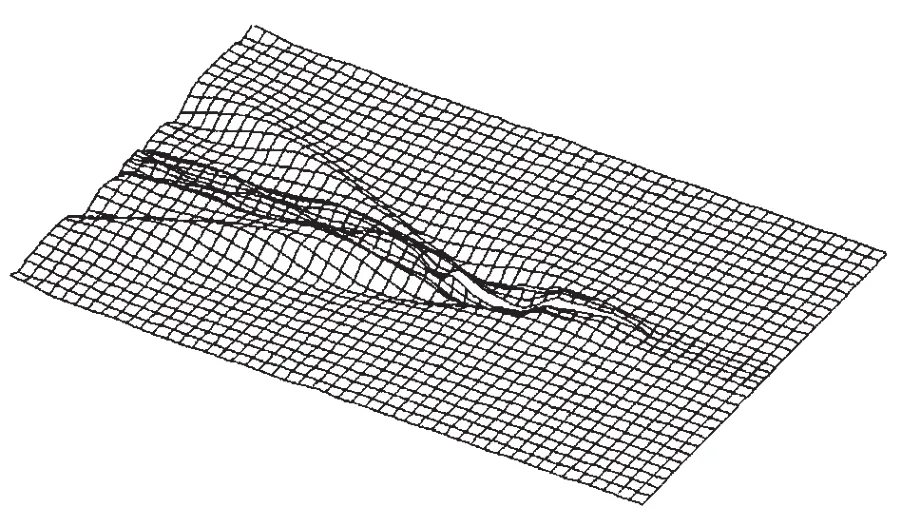
图13 三维波形图(Xs=-0.2L,Ys=9 m,Fn=0.6)Fig.13 Three dimensional wave pattern of triamaran(Xs=-0.2L,Ys=9 m,Fn=0.6)
5 结 语
本文所采用基于NURBS的广义高阶面元法对于三体船兴波波形与兴波阻力的数值计算可以反映三体船的兴波特性,得到较为合理且优于薄船理论的计算结果。对于高速方尾三体船侧体的横向偏距和纵向偏距对兴波阻力影响的初步计算结果与其他学者的研究结果基本一致。今后将对有关的非线性问题作进一步的研究探讨。
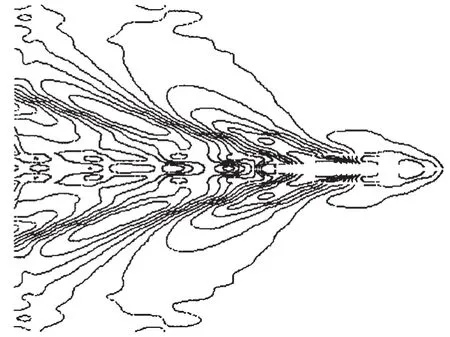
图14 三维波形等高线图(Xs=-0.2L,Ys=9 m,Fn=0.6)Fig.14 Contour map of three dimensional wave pattern for triamaran(Xs=-0.2L,Ys=9 m,Fn=0.6)
[1]Elcin Z.Wave Making Resistance Characteristics of Trimaran Hulls[D].Monterey,CA:Master’s Thesis,Naval Postgraduate School,2003.
[2]Yang C,Noblesse F,Lohner R.Practical hydrodynamic optimization of a trimaran[C]//SNAME Annual Meeting.Orlando,FL,2001:185-196.
[3]陈京普,朱德祥,何术龙.双体船/三体船兴波阻力数值预报方法研究[J].船舶力学,2006,10(2):23-29.
Chen Jingpu,Zhu Dexiang,He Shulong.Research on numerical prediction method for wavemaking resistance of catamaran/trimaran[J].Journal of Ship Mechanics,2006,10(2):23-29.
[4]高 高,马 岭,邹早建.排水型高速双体船兴波问题的数值计算[J].武汉理工大学学报,2003,25(6):586-596.
[5]高 高.船波问题的辐射条件、自由面条件的研究及面元法误差分析[D].武汉:武汉交通科技大学,1997.
[6]Suzuki K,Kai H.Numerical estimation of wave making characteristics of high-speed ships taking sinkage and trim effects into account[C]//International Conference on Fast Sea Transportation,FAST’2005,June 2005.St.Petersburg,Russia,2005.
[7]Gao Gao.Numerical implementation of transom conditions for high-speed displacement ships[J].Journal of Ship Mechanics,2006,10(3):1-9.
[8]Nakos D E,Sclavounos P D.Kelvin wake and wave resistance of cruiser-and transom-stern ships[J].Journal of Ship Research,1994,38(1):9-29.
[9]李培勇,裘泳铭,顾敏童,王文富.三体船阻力模型试验[J].中国造船,2002,43(4):6-12.
[10]Tuck E O,Lazauskas L.Optimum hull spacing of a family of multihulls[J].Applied Mathematics Publications,1998,45:180-195.
[11]郦 云,卢晓平.高速三体船阻力性能研究[J].船舶力学,2007,11(2):191-198.
Li Yun,Lu Xiaoping.An investigation on the resistance of high speed trimarans[J].Journal of Ship Mechanics,2007,11(2):191-198.
