半潜平台载荷不确定性及结构可靠性研究

杨 鹏，顾学康，吴东伟

（1中国船舶科学研究中心，江苏 无锡 214082；2中国舰船研究设计中心，武汉430064）

1 引 言

随着海洋油气资源开发向深海的不断迈进，现代半潜式海洋平台已经发展到了第六代，作业水深达到3 000m以上。半潜式海洋平台的制造成本和维护成本十分昂贵，而且一旦发生事故，不仅人员生命和经济的损失巨大，对环境的污染也是相当严重的。巴西平台倾翻和墨西哥湾漏油事件已经给人们以深刻教训，因此海洋平台的结构安全性评估显得尤为重要。半潜平台结构几何尺度、材料特性和制造工艺存在很多不确定性因素，外载荷的不确定性尤为显著。传统的确定性强度评估手段在平台结构的安全性设计校核中存在缺陷，必须进行基于概率方法的可靠性评估以提高海洋工程结构的安全性。

目前，波浪载荷的不确定性计算仍未得到很好的解决，主要原因是波浪载荷不确定性涉及到诸多不确定性因素，如海浪谱型的不确定性、波高的不确定性和载荷传递函数的不确定性等。如何合理地确定波浪载荷和结构承载能力的统计参数及其不确定性是本文要解决的主要问题，文中分析了海浪谱型、波高对波浪载荷的影响，运用模型试验和数值计算方法分析了波浪载荷传递函数的不确定性，提出了波浪载荷长期极值不确定性分析的新方法。接着使用蒙特卡洛模拟法和改进的Rosenbluth方法同时计算结构极限承载能力的统计参数及其不确定性。最后基于计算的统计参数使用验算点法计算了某半潜平台结构可靠性。

2 波浪载荷的不确定性分析

波浪载荷长期极值分析的不确定来源主要有：（1）海浪长期散布图的不确定性；（2）海浪谱型的不确定性；（3）有义波高与跨零周期的不确定性；（4）载荷传递函数的不确定性；（5）波浪载荷短期和长期预报模型的不确定性，等等。

海浪谱型、波高和载荷传递函数对波浪载荷短期预报和长期预报的影响可以归结为对波浪载荷均方响应的影响，即载荷响应谱的0阶矩，其可以表示为：

式中：S（ ωi,Hs,Tz）为海浪谱，H（ ωi,α）为浪向 α 度时的波浪载荷响应传递函数。

当综合谱型、传递函数以及波高不确定性因素的影响时，应建立起较完整的长期分布函数和长期超越概率函数形式，Soares[1]考虑这些不确定性后，给出如下超越概率方程：

式中：W （TZ）为权重函数，W（ TZ）=T0/TZ，TZ为特定短期海况的平均周期，T0为所有海况的平均周期：

R0为单位波高下的波浪载荷均方响应，fR（α, HS,TZ）为浪向、波高和周期的联合概率密度函数，p（ HS,TZ）为海况发生概率。φT为综合考虑了谱型、传递函数以及波高不确定性影响的各短期载荷相应0阶矩的总偏差系数，并且认为不同的不确定性影响因素之间是相互独立的。根据公式（1）得到载荷0阶矩总偏差系数的均值和COV为：

2.1 海浪谱型的不确定性分析

谱型不确定性可简单理解为对于一个短期海况 （Hs, Tz），如果采用不同海浪谱来描述，那么相应计算结果是不同的。由于计算中采用的海浪谱一般为理论的谱型公式，与实际海浪情况会存在差别，从而引入了一系列的不确定性因素。目前工程界推荐的海浪谱有P-M谱，JONSWAP谱，双峰谱等等。

平台波浪载荷均方响应（mean square response）即响应谱的0阶矩，可以表示为：

式中：H（ ωi,α）为浪向 α 度时的平台载荷响应传递函数，θi表示不同的谱型，εi为零均值正态分布的随机变量。

载荷均方响应R也是正态分布的随机变量，其均值和变异系数为：

Haver等[2]通过对船舶载荷响应计算和分析指出，当谱间隔为0.01Hz时，均方差σε的值可取为0.5～0.55。如果为了更好地描述波谱而选择较小的谱频率间隔，那么应该适当增大σε值。

以上是采用一个谱型来描述一个浪向下的载荷响应时产生的不确定性，给出了均方响应的均值E[ R （ θ）]和方差Var[ R （ θ）]的表达式。因谱型的不同而产生的不确定性可以用多个载荷响应谱的0阶矩加权来描述，每个谱型将对应一个条件概率，那么总的均值和方差为：

式中，θ表示不同谱型，fθ表示不同谱型出现概率，可见R的不确定性来自于谱型本身的不确定性和谱型之间的差别。采用标准谱型的载荷均方响应值可以用如下方法确定：

其中：S（ω）可选择ISSC双参数谱（即P-M谱），H（ω）取数值计算所得的传递函数。

于是，相对于标准谱方法的偏差系数（Bias）表示为：

这里φS与R分布形式相同，也是正态分布变量，该偏差系数均值和变异系数为：

本文选择P-M和JONSWAP谱来综合模拟实际海浪，分析波谱表达式对谱型不确定性的影响。根据Soares[1]的分析结果，北大西洋海况中PM谱的发生概率为：p （Hs）=0.86-0.06Hs，Hs≤14.33m；p （Hs）=0，Hs>14.33m。 σε值取0.525，JONSWAP谱的谱峰提升因子取3.3，将标准谱设定为P-M谱。列出某半潜平台生存工况下 （HS=13.7m，TZ=11.89s）六种主要总体载荷[3]不确定性分析结果，如表1和 2。

表1 谱型偏差系数的均值和变异系数（1）Tab.1 Mean value and COV for spectrum bias(1)

从表1和2可以发现生存工况下谱型偏差系数的均值在 0.91～1.01之间，COV在0.13～0.22之间。可见谱型偏差系数的均值接近于1，而COV较大，说明谱型不确定性主要引起较大的离散性。

表2 谱型偏差系数的均值和变异系数（2）Tab.2 Mean value and COV for spectrum bias(2)

2.2 波高的不确定性分析

Soares[1]在前人的观测数据和理论分析的基础上，经过细致总结，给出了北大西洋

真实有义波高值HS和观测值HV之间的回归方程：

式中：HV一般从海况资料中选取；ε为服从零均值正态分布的随机变量，其标准差为s。

那么波高偏差系数的均值和变异系数为：

根据公式（1）可知波浪载荷均方响应与波高的二次方成正比，那么由波高不确定性导致的波浪载荷均方响应的偏差系数均值为：

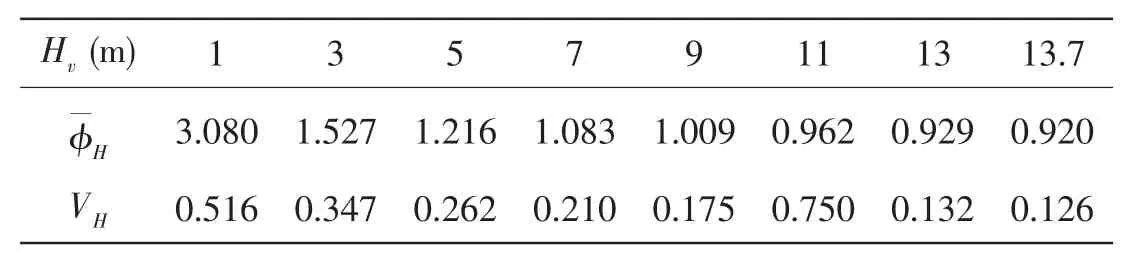
表3 Soares公式计算结果Tab.3 Result in Soares’s formula

根据公式（16）和（17）计算波高偏差系数的均值和COV，得到表3结果。

本文根据方钟圣等[4]统计的西北太平洋有义波高海况资料 （见表4和5）， 使用HS和 HV均值拟合出 Hs和 Hv之间的关系式：

表4 浮标测量结果（Hs）Tab.4 Measurement result of buoy

式中：ε为服从零均值正态分布的随机变量，其标准差为s待定。

由概率论可知HS和HV的方差关系为：

表5 船舶观测结果（Hv）Tab.5 Visual result of ship

由表4和表5中的HS和HV的标准差可以得到σε，见表6。

表 6 ε的标准差Tab.6 Mean variance of ε

从表3和表7的比较可以看出，本文总结的波高公式比Soares公式计算的COV小。可能原因在于本文计算公式回归的是西北太平洋的波高统计资料，而Soares回归统计的是北大西洋的海况资料，后者的海况偏于恶劣，统计离散性和各有义波高下标准差较大。

表7 西北太平洋计算结果Tab.7 Result in northwest Pacific

图1 水池模型试验Fig.1 Model trial in tower

2.3传递函数的不确定性分析

为了合理考察半潜平台波浪载荷传递函数的不确定性，需要开展半潜平台波浪载荷模型试验研究。某半潜平台的波浪载荷模型试验在中国船舶科学研究中心耐波性水池进行，模型缩尺比40，试验模型如图1。

90°浪向下横垂向弯矩和水平分离力传递函数的数值计算结果（SESAM）和模型试验结果比较如图2和3，可以发现，横垂向弯矩和水平分离力的试验结果和数值结果比较吻合，下面针对横垂向弯矩和水平分离力的传递函数进行不确定性分析。Sagli[5]通过敏感性分析指出，传递函数的首尾部分对长期极值的影响较小，因此只需分析传递函数峰频区域。对图2和3的峰频区域采用样条插值拟合如图4和5。以试验结果作为真实值，理论预报计算值作为理论值来估计偏差系数的均值和变异系数，结果如表8。由于在试验过程中，测量系统存在一定的系统误差和不确定性，同时横垂向弯矩引起的结构应力会远大于水平分离力引起的结构应力。这样水平分离力的测量信号会较小，其测量误差很可能是大于横垂向弯矩的，表8中水平分离力COV大于横垂向弯矩的COV证实了这一点。

图2 水平分离力Fig.2 Horizontal split force

图3 横垂向弯矩Fig.3 Transverse vertical moment

图4 水平分离力Fig.4 Horizontal split force

图5 横垂向弯矩Fig.5 Transverse vertical moment

以横垂向弯矩传递函数的偏差系数的均值和COV为参考，纵垂向弯矩、纵向剪力、横向扭矩及垂向剪力传递函数的偏差系数均值和COV取相同值，而水平分离力传递函数的偏差系数均值和COV分别取0.76和0.17，并将这些数据推广到各个浪向。同时根据公式（1）可知波浪载荷的均方响应与载荷传递函数的平方成正比。

2.4 长期预报的不确定性研究

Sagli[5]曾指出长期极值的不确定性可以由试验传递函数的峰值和理论预报的峰值之比来衡量，其实这仅简单地考虑了传递函数不确定性对长期极值的影响。利用公式（4）和（5）计算各短期响应偏差系数的均值和变异系数。表9和10给出了生存工况（Hs=13.7m，Tz=11.89s）下六种典型载荷的三个浪向计算结果。

从表9和10可以看出除了横向分离力，其他五种载荷偏差系数均值绝大多数在0.96～1.18之间，COV在0.37左右。横向分离力的偏差系数均值基本在0.47左右，COV在0.46左右。横向分离力和其他载荷的偏差系数的均值和COV之所以会有这么大的差别，主要在于横向分离力传递函数的偏差系数的均值和COV与其他载荷传递函数的有很大不同。

进行海浪谱型、波高和载荷传递函数的不确定性对载荷影响比重研究也是很有意义的，表11和表12分别给出了生存海况下这三个不确定因素对短期载荷偏差系数均值和COV的影响比重。

表8 载荷传递函数偏差系数的均值和变异系数Tab.8 Mean value and COV for uncertainty of load transfer function bias

表9 短期响应偏差系数的均值和变异系数（1）Tab.9 Mean value and COV in short-term loads bias(1)

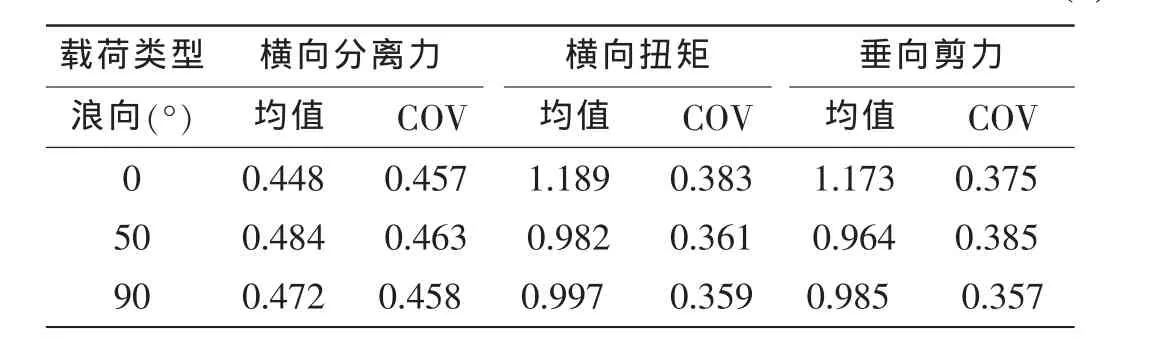
表10 短期响应偏差系数的均值和变异系数（2）Tab.10 Mean value and COV in short-term loads bias(2)

表11 谱型、波高和载荷传递函数不确定性对COV影响比重Tab.11 Weight influence of COV due to uncertainty for spectrum,wave height and load transfer function

表11中数据表明，从短期载荷偏差系数的COV角度出发，谱型的不确定性对短期载荷偏差系数的影响相对较小，而波高的不确定性对短期载荷系数影响最大，传递函数次之。而表12中数据表明，从短期载荷偏差系数的均值角度出发，谱型的不确定性对短期载荷偏差系数影响相对较小，而传递函数的不确定性对短期载荷系数的影响最大，波高次之。

短期响应的不确定性对长期结果的影响是载荷不确定性研究中的重要内容，下面给出Soares提出的长期结果不确定性计算方法和本文提出的方法，并对两种方法的计算结果进行比较分析。当φT取均值时，方程（2）即为长期预报超越概率的平均分布（x），对应的长期特征值为。当φ=1.0 时，方

表12 谱型、波高和载荷传递函数不确定性对均值影响比重Tab.12 Weight influence of mean value due to uncertainty for spectrum,wave height and load transfer function

T程（2）为无偏的标准超越概率分布形式，对应10-8长期超越概率下的长期预报值为xcs。可以确定10-8超越概率下长期预报值的偏差系数均值为：

将方程（2）代入（22）式中，得到：

Soares方法通过超越概率的标准差得到长期预报极值的标准差，缺乏严密的数学基础，计算结果也不合理。本文将长期超越概率方程中x表示成QLT（x）的函数，直接求解对应超越概率下x的变异系数，数学上更为严密。x的方差和变异系数为：

在10-8的超越概率下，使用北大西洋海浪谱，针对六种典型载荷给出Soares方法和本文方法[6]计算结果对比，如表13。

表13 载荷长期预报的均值和变异系数Tab.13 Mean value and COV in long-term load prediction

从表13中可以看出Soares的计算结果比本文方法的计算结果明显偏小。本文方法计算的各项COV基本上在0.21～0.25之间，偏差系数均值在1.14左右，除了横向分离力的偏差系数为0.77。

2.5 载荷长期极值分布的不确定性

波浪载荷长期极值分布可由Gumbel分布较好地描述，Gumbel分布本身的不确定性变异系数为：

如果已知初始Weibull的形状参数r及超越概率，则易得Gumbel分布本身的理论变异系数VYn，那么长期极值总的变异系数为：

式中：Vx为一定长期超越概率下的载荷响应变异系数。

式中：u为初始Weibull分布的长期最可能极值。f（x），F（x）为初始Weibull分布的概率密度和概率分布函数，r和k分别为初始Weibull分布形状参数和尺度参数，N为载荷总的循环次数。

3 结构极限承载能力不确定性研究

3.1 结构极限承载能力的不确定性

一般来说结构极限强度的分布形式是未知的，通常需要使用解析的概率分布形式去拟合,以便后续分析。工程上常用直接蒙特卡洛法进行模拟，生成大量样本点，最后对样本空间使用已知的解析函数进行拟合，从而得到合理的分布形式。

何福志等[7]详细分析了简化的Smith方法，并考虑了硬角单元选取、单元应力应变关系和腐蚀对极限承载能力计算结果的影响。而祁恩荣等[8]使用Smith方法计算某大型液化天然气船船体极限强度，根据和其他几种计算方法比较，认为Smith方法是较为合理的。很多文献都使用简化的Smith方法计算船舶结构极限强度，本文推广该方法用于计算某半潜平台横垂向弯矩极限承载能力。每个加筋板单元有三个随机变量：板厚t，弹性模量E，材料屈服应力σy。Hess等[9]对普通强度钢和高强度钢分别进行了统计分析，其给出的普通强度钢的变异系数为0.124，高强度钢的变异系数为0.083，分布类型可取正态分布或对数正态分布。Mansour等[10]分析了近300个试样的弹性模型的测量数据后得出：结构弹性模型的变异系数（COV）加权平均值为0.031，均值为2.06×1011Pa。Stiansen[11]建议变异系数取为0.01～0.02，分布类型可取正态分布或对数正态分布。Hess等[9]在Mansour的基础上进行了更加完善的总结分析。本文选取板厚COV=0.06，服从正态分布；材料屈服应力COV=0.08，服从对数正态分布；弹性模量COV=0.03，服从正态分布。

图6 蒙特卡洛法模拟结果Fig.6 Simulation result of Monte Carlo method

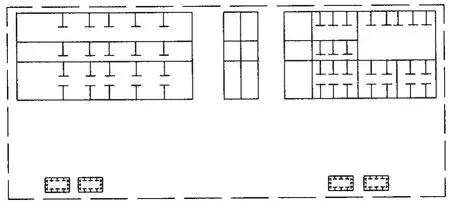
图7 中纵剖面结构Fig.7 Middle longitudinal structure

使用直接蒙特卡洛模拟法得到某半潜平台结构横垂向弯矩极限承载能力，模拟次数为1E5次。分别使用正态分布和对数正态分布来拟合分析样本点的分布形式，从图6中的曲线形状来看，使用正态分布或对数正态分布拟合均合适，但是对数正态分布对右端尾部的拟合更好，因此本文选用对数正态分布拟合结构极限承载能力。中垂均值为 1.21E10（N·m），COV=0.09， 中拱均值为 1.08E9 （N·m），COV=0.08。中纵剖面结构图见图7。结构极限承载能力均值和方差也可以通过改进的Rosenbluth方法[12]得到，改进的Rosenbluth方法计算量小，而且精度达到了二阶Taylor级数的精度。徐向东[13]和祁恩荣[14]等分别使用改进的Rosenbluth方法来计算船舶极限强度和剩余极限承载能力，从理论推导和计算分析中论证了该方法合理性。本文使用改进的Rosenbluth方法计算某典型半潜平台结构极限承载能力如下：中垂均值为1.24E10（N·m）， COV=0.09；中拱均值为 1.07E9（N·m），COV=0.08。可见直接蒙特卡洛模拟法和改进的Rosenbluth方法计算结果是比较吻合的。

3.2 静水载荷的不确定性

由于半潜平台全寿命期内静水载荷的变化比一般船舶小得多，因此可以参照排水量变化较小的舰船的静水弯矩变异性数据，初步选择平台静水弯矩的COV=0.10，偏差系数为1.0，即静水弯矩的均值即是名义值。经计算，平台横向的静水弯矩正态分布的均值为1.09E9N·m，COV=0.10。

4 结构极限强度可靠性计算

半潜平台中纵剖面的横向结构比较薄弱，所以平台横向结构在波浪载荷下的极限强度可靠性问题比总纵强度更为重要。由于横向静水弯矩大多产生中垂的效果，所以在中拱极限强度可靠性分析中，不计静水弯矩，这样处理使得中拱极限强度可靠性指标相对保守。平台横向总体强度的极限状态方程如下：

（1）中拱极限状态方程：Z=MHU-MW。

（2） 中垂极限状态方程：Z=MSU-MW-MS。

式中：MHU中拱极限弯矩，MSU中垂极限弯矩，MW波浪弯矩，MS静水弯矩。

平台结构与载荷统计参数见表14，使用验算点法计算的可靠性结果见表15。从验算点灵敏度系数可以看出极限状态方程对波浪载荷最为敏感。

表14 平台结构与载荷统计参数Tab.14 Statistical parameters of structure and load

有学者建议目标可靠性指标可根据结构失效类型和失效后果进行确定[15]，从本文计算的半潜平台可靠性的评估结果可以看出，中垂中拱的可靠性指标（见表15）比推荐的目标可靠性指标4.26要高，也即该半潜平台强度储备能力较高，结构是安全的。

表15 可靠性计算结果Tab.15 Calculation result of reliability

5 结 论

本文详细分析了海浪谱型、波高和载荷传递函数的不确定性对短期载荷和长期载荷的影响，认为海浪谱型的不确定性对短期载荷系数影响是较小的，而波高的不确定性对短期载荷系数影响最大，载荷传递函数次之。同时给出了生存工况下短期载荷和全海况长期载荷偏差系数的均值和方差，建立了一套分析和计算短期预报、长期预报及长期极值统计参数的评估方法。最后通过计算实例评估了某典型半潜平台结构极限强度可靠性。

为了建立更完善的评估手段，需要统计分析更多数量和类型的海洋平台数据，从而得出大量短期预报、长期预报和长期极值预报的统计参数及其不确定性，归纳出合理的工程实用系数，为工程实践和相关标准制定提供可靠依据。

[1]Soares C G.Probabilistic models for load effects in ship structures[D].Ph.D.Thesis.Norwegian Institute of Technology,NTH,Trondheim,Norway,1984.

[2]Haver S,Moan T.On some uncertainties related to the short term stochastic modeling of ocean waves[J].Applied Ocean Research,1983,5:93-108.

[3]DNV-RP-C103.Column-stabilized units[S].DET NORSKE VERITAS,2005.

[4]方钟圣,金承仪,缪泉明.西北太平洋波浪统计集[M].北京:国防工业出版社,1996.

[5]Sagli G.Model uncertainty and simplified estimates of long term extremes of hull girder loads in ships[D].Ph.D.thesis.NTNU,Trondheim,Norway,1998.

[6]吴东伟.半潜平台结构强度可靠性评估方法研究[D].无锡:中国船舶科学研究中心,2011:70-72.

[7]何福志,马建军,万正权.船体结构总纵极限强度的简化逐步破坏分析方法[J].中国造船,2005,46(2):17-27.

[8]祁恩荣,张晓杰,等.大型液化天然气船船体极限强度研究[J].船舶力学,2010,14(1-2):66-73.Qi Enrong,Zhang Xiaojie,et al.Study of ultimate hull girder strength of large liquefied natural gas carriers[J].Journal of Ship Mechanics,2010,14(1-2):66-73.

[9]Hess P E,Daniel B,Ibrahim A A,et al.Uncertainties in material strength,geometric,and load variables[J].ASNE Naval Engineer Journal,2002,114:139-165.

[10]Mansour A E,Jan H Y,Zigelman C I.Implementation of reliability methods to marine structures[J].Trans.Society of Naval Architects and Marine Engineers,1984,92:11-20.

[11]Stiansen S G,Mansour A E.Ship primary strength based on statistical data analysis[J].Trans.SNAME,1975,83:214-243.

[12]Cui W C.On consistent determination of structural capacity statistics for reliability analysis[J].Journal of Ship Mechanics,2002,6(3):37-51.

[13]徐向东.基于极限强度的船体结构可靠性分析与设计[D].无锡:中国船舶科学研究中心,1998.

[14]祁恩荣.完整和破损船体极限强度可靠性研究[D].无锡:中国船舶科学研究中心,2003.

[15]桑国光,张圣坤.结构可靠性原理及其应用[M].上海:上海交通大学出版社,1987.