主成分分析法(PCA)在SIFT匹配算法中的应用

马 莉，韩 燮

(中北大学电子与计算机科学技术学院，山西 太原 030051)

David G.Lowe于2004年提出了基于尺度不变特征变换(SIFT)的特征提取算法。此算法的基本特性是稳定，它对于不同场景、不同光照、不同几何形状变换都具有较强的稳定性，提高了匹配的精确度[1]。但算法仍然存在一些不足，比如特征描述符的维数过大以及耗时过长。在原始的SIFT特征提取算法中融入一种主要用于对数据进行降维的主成分分析法(PCA)，就得到一种基于主成分不变特征变换(PCA－SIFT)的特征提取算法[2]，PCA－SIFT算法既继承了传统SIFT算法稳定性和多量性的优点，又利用主成分分析法降低了传统SIFT特征描述符向量的维数，提高了匹配效率。

1 生成SIFT特征描述符

SIFT算法要在尺度空间和二维平面空间中同时进行极值检测以找出局部极值点，并且对所提取出的关键点进行精确的定位，然后根据此关键点所处位置周围邻域点的梯度方向计算出该关键点的主方向[3]，以实现算子对几何变换和旋转的不变性。一般生成SIFT特征描述符需要几个步骤:1)尺度空间的建立;2)计算关键点特征方向，进行特征点定位;3)SIFT特征描述符的向量表示。

1.1 尺度空间的建立

Koenderink证明了高斯卷积核是实现尺度变换的唯一线性变换核[4]。二维的高斯函数定义为

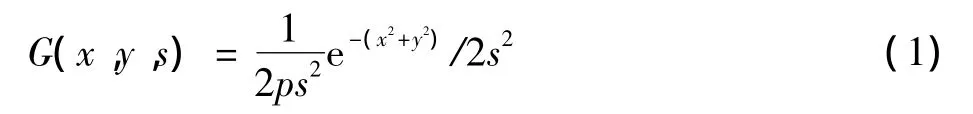
式中:(x，y)是空间坐标。那么，一副图像的二维尺度空间就可以由图像和高斯核卷积得到

特征点的检测要在尺度空间和平面空间中同时进行，这样才可以确保得到稳健性强的特征点。因此就引入了DoG算子，它是两个不同尺度高斯核的差分值[5]，DoG算子的构成为

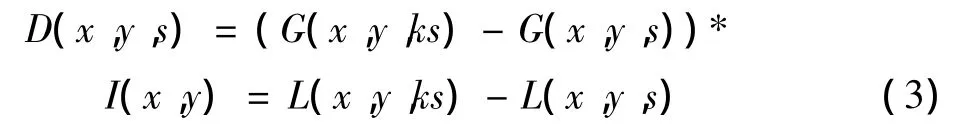
接下来就要构建一个大小为O组，并且每组中由S层图像构成的图像金字塔，组与组之间的关系为:上一组的图像降采样得到下一组图像。在构建好图像金字塔的基础上，进行局部极值检测，其中每一个像素都需要跟同一平面中的其他8个像素和相邻尺度空间中该像素所对应位置的9×2个像素进行计算比较[6]，只有被检测像素点的高斯核差分值(即DoG值)都大于或都小于与它进行比较的26个像素的DoG值时，才能把此点作为一个局部极值点。

1.2 计算关键点的特征方向

为了使所提取的特征点具有缩放和旋转不变性，就要利用每个关键点周围邻域的其他点来计算此关键点的特征方向。其中关键点处梯度模值的计算如式(4)所示，关键点主方向的计算如式(5)所示

1.3 SIFT特征描述符的向量表示

如图1所示，对每一个筛选出的特征点，要以此特征点作为中心点，在这个点的周围选取一个大小为16×16的区域，再将这个所选取区域平均分成4个大小均为4×4的小区域，并且计算每个小区域的梯度直方图，直方图包含有8个bin方向，这样就获得了一个4×4×8=128维的向量，也就是生成了SIFT特征描述符向量，直方图的峰值就是所选特征点的主方向。

图1 SIFT特征描述符的向量表示示意图

2 PCA－SIFT特征描述符的建立

PCA－SIFT描述符与标准SIFT描述符具有相同的亚像素位置(Sub－pixel)、尺度(Scale)和主方向(Dominant Orientations)，但在特征描述符生成时有所不同，PCASIFT用主成分分析法(PCA)将传统SIFT的128维特征向量进行降维，以达到更精确的表示方式。利用主成分分析法对传统的128维SIFT特征描述符进行降维的具体方法如下:

1)输入两幅待匹配图像中所有关键点(设为n个)的128维SIFT特征描述符，将输入的这n个特征描述符作为样本，写出样本矩阵为[x1，x2，...，xn]T，其中 xi表示第 i个特征点的128维特征向量。

3)计算所有样本点的特征向量与平均特征向量的差，得到差值向量

5)求协方差矩阵的128个特征值λi和128个特征向量ei。

6)将求出的128个特征值按从小到大的顺序进行排列λ1≥λ2≥…≥λ128和对应的特征向量[e1，e2，…，e128]。

7)选取对应t个最大特征值的特征向量作为主成分的方向，在实验中选取t=20。

8)构造一个128×t的矩阵A，它的列由t个特征向量组成。

9)把原始的128维SIFT描述符依据式(6)投影到所计算出的n维子空间M中，就可以得到PCA－SIFT的描述符 y1，y2，…，yn了，即

因为实验中选取t=20，所以矩阵A的大小为128×20，xi的大小为1×128，所以xi*A就得到了一个大小为1×20的矩阵，即每一个yi就是一个20维的特征描述符，也就是把原来的128维传统SIFT特征描述符降成了20维的 PCA－SIFT 特征描述符[6]。

3 基于PCA－SIFT特征提取算法的图像匹配

3.1 对应特征点的匹配

当对两幅待匹配图像分别使用PCA－SIFT特征提取算法找出各自的特征点并进行精确定位，生成对应的特征描述向量后，就可以计算特征向量间的欧式距离，两个特征向量之间的欧式距离值越小，就说明这两个点越相似，它们的匹配程度就越高。欧式距离的计算如式(7)所示

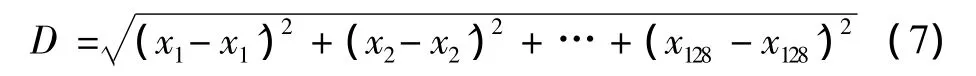
式中:(x1，x2，……，x128)，(x'1，x'2，……，x'128)分别为待匹配两幅图像上的关键点所生成的特征向量。首先找出其中一幅图像中的某个关键点，采用遍历的方法在另外一副图像中找出与这个关键点欧式距离最近和次近的两个关键点，如果最近的距离与次近的距离的比值小于某个阈值，那么认为这一对点就是一对匹配点。在实验中选取阈值为0.6，如式(8)所示

式中:Dnearest为最近欧式距离，Dhpyo－nearest为次近欧式距离。

3.2 消除错误匹配

在实验中由于环境因素和遮挡因素，有可能出现错误的匹配，为了提高匹配的正确性和稳健性，需要采取一些措施来保证匹配的正确率。RANSAC算法是一种依靠对数据进行拟合的算法，它具有很强的稳健性，首先要在分析具体问题的前提下，设计出某种适合这个问题的目标函数，然后反复进行迭代来估计该数学函数模型中参数的初始值，继续利用求出的初始参数值把所有的数据分为满足该模型参数的“内点”和不满足该模型参数的“外点”，最后反过来用所有满足该模型参数的“内点”重新对模型参数进行估计，最终得到精确的匹配结果，消除错误匹配[7]。

3.3 变换模型参数的估计

假定以图像1(I1)作为参考系，将图像2(I2)变换到图像1所在的坐标系，变换后的图像为I'2，则其对应关系为

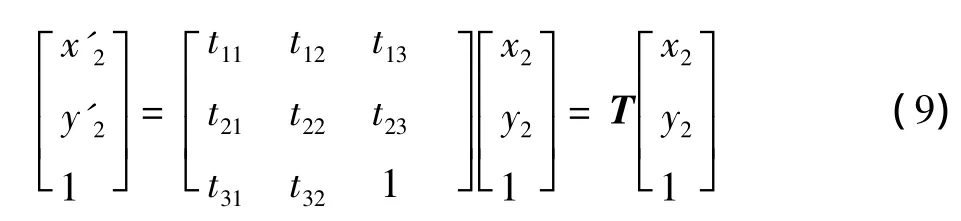
式中:(x，y)和(x'，y')是一对匹配点，只需4对匹配点即可算出T，得到T后，就可确定这8个参数。这8个参数决定了两幅图像坐标之间的转换关系，确定其值后就可以得到精确的图像匹配结果。

4 实验结果及分析

实验环境为 CPU Pentium 2.94 GHz，内存 1.5 Gbyte，显存为128 Mbyte，操作系统为Windows XP，仿真平台为Matlab 7.1，所用的图像采集设备为Bumblebee双目视觉相机。使用了不同场景下的图像进行实验，包括光照、旋转、缩放等情况。在这些不同的情况下进行实验并对传统的SIFT算法和改进后的PCA－SIFT算法在匹配的正确率和匹配所用的时间上进行比较(实验结果见图2～图5，表1～表4)。

图2 不同算法下的匹配结果图(截图)

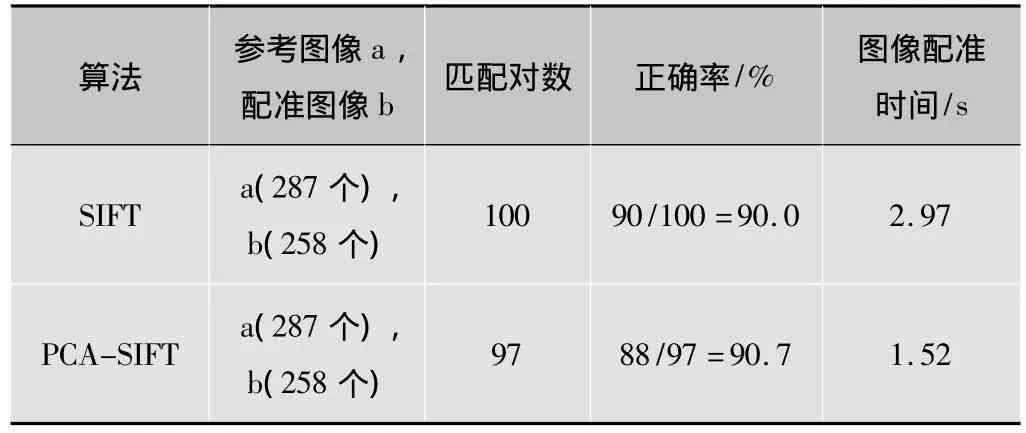
表1 原图使用SIFT和PCA－SIFT匹配结果的比较

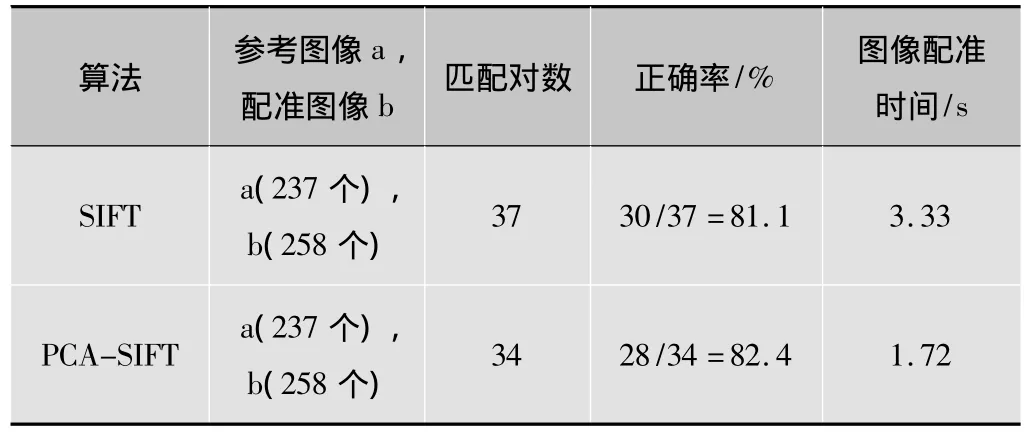
表2 光照改变时使用SIFT和PCA－SIFT匹配结果的比较

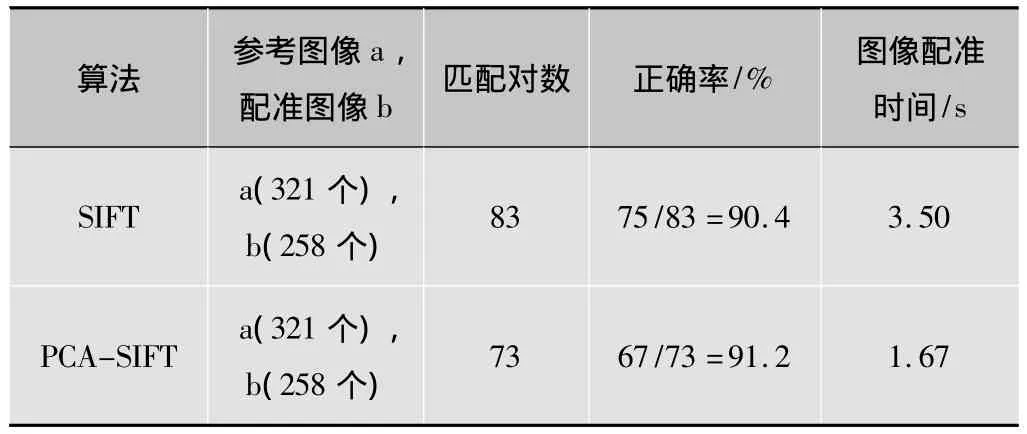
表3 旋转时使用SIFT和PCA－SIFT匹配结果的比较

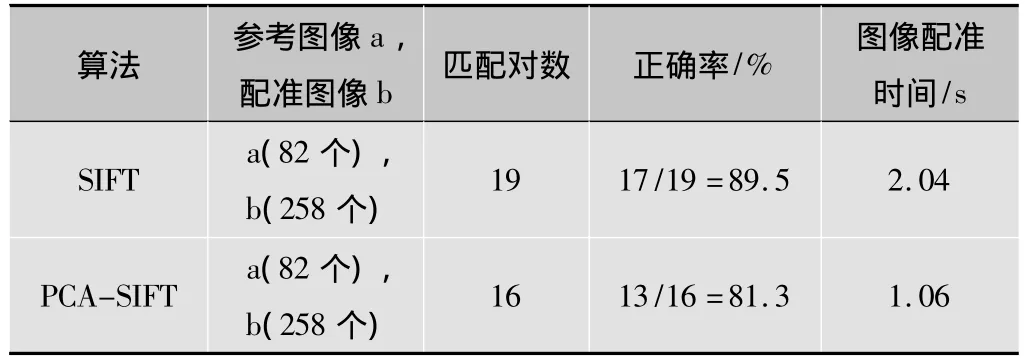
表4 缩放时使用SIFT和PCA－SIFT匹配结果的比较

根据表1～表4，可以得出以下结论有:1)在匹配的正确率方面。无论图像是在光照改变，旋转，还是在缩放的情况下PCA－SIFT都具有很稳定的匹配性能;2)在匹配的时间方面。基于PCA－SIFT的匹配算法使得匹配的时间有所降低，提高了匹配的效率。

从实验结果中可以看出基于PCA－SIFT描述符的匹配算法和基于传统SIFT特征描述符的匹配算法在各种情况下的正确率都基本上相当，但是在时间上PCA－SIFT算法却大大地节约了匹配时间，这就说明PCA－SIFT算法既保持了SIFT算法稳定性和精确性，又减少了匹配时间。

5 小结

把主成分分析法引入到传统的SIFT匹配算法中，把特征描述符的维数从128维减少到20维，减少数据量，节约了整个匹配算法的运行时间。实验证明PCA－SIFT算法既保持了传统SIFT算法的稳定性和精确性的优点，又比传统的SIFT算法有一定程度的改进。

[1]周峰.基于尺度不变特征变换(SIFT)的图像配准技术研究[D].昆明:昆明理工大学，2010.

[2]吴若鸿.基于特征匹配的双目立体视觉技术研究[D].武汉:武汉科技大学，2010.

[3]徐秀云.基于特征点的景象匹配技术研究[D].南京:南京理工大学，2009.

[4]冯嘉.SIFT算法的研究和改进[D].长春:吉林大学，2010.

[5]PLUIM J P W，MAINTZ J B A，VIERGEVER M A.Mutual information matching in multiresolution contexts[EB/OL].[2011－06－12].http://www.docin.com/p－43905533.html.

[6]COPPINI G，DICIOTTI S.Matching of medical images by self－organizing neural networks[J].Pattern Recognition Letters，2004，25(3):341－352.

[7]FLUSSER J，SUK T.A moment－based approach to registration of images with affinegeometric distortion[J].IEEE Trans.Geo－Science and Remote Sensing，1994，32(2):382－387.