影响频率选择表面传输特性的参数分析＊

郭兴旺 李尚生 陈佳林

（海军航空工程学院电子信息工程系 烟台 264001）

1 引言

频率选择表面（Frequency Selective Surface，简称FSS）是一种二维周期结构，它最本质的特征就是能够对不同频率、入射角及极化状态下的电磁波呈现滤波特性。频率选择表面的周期单元大致分为两种类型，一种是金属贴片，另一种是导体屏周期开孔（缝隙），通常FSS需要介质层支撑和覆盖。当频率选择表面的谐振单元处于谐振状态时，处于谐振频率的电磁波被全反射（单元为贴片型）或全透射（单元为缝隙型）。频率选择表面在降低重要回波源的雷达散射截面（RCS）方面具有广泛的应用，这使其成为近几十年来电磁学研究领域的热点问题。

针对FSS电磁特性的分析方法主要有周期矩量法［1］、基于Floquet定律求解未知孔的电磁场的模式匹配法［2～5、等效电路法［6～9］等，其中等效电路法是一种古老的方法，对于复杂的FSS结构是无能为力的。虽然有如上所述诸多的方法可以对FSS的传输（反射）特性进行分析，但是每一种方法都涉及到复杂的理论与算法，详细深入地学习这些方法对于仅仅关心FSS应用的工程技术人员来说无疑是非常头疼的一件事。到目前为止，虽然人们在寻找计算FSS谐振频率的简单方程或方法方面已经付出了很大努力，但是没有一种方法简单可行。为此，本文分析了FSS主要结构参数对其传输（反射）特性的影响，为该研究领域的工程技术人员提供了一个直观、简明的参考。

实际应用中的FSS都有介质作为支撑，有一定的几何形状，单元分布有一个固定的周期，这些因素共同决定了该结构的电磁特性。因此，本文以两侧有对称介质支撑的平面无限大单层圆环缝隙FSS为例，通过HFSS软件进行仿真［10］，分析了介质参数、单元周期、圆环半径等参数对该FSS传输特性的影响。

2 FSS模型

本文的所有算例都是基于图1所示圆环缝隙结构进行参数修改后的模型，该结构单元周期为16mm＊16mm，内圆环半径为4mm，外圆环半径为4.8mm，圆环缝隙金属板的两侧各有1mm厚介质，介质无损耗，相对介电常数为1.0（等效于空气），如图1所示。

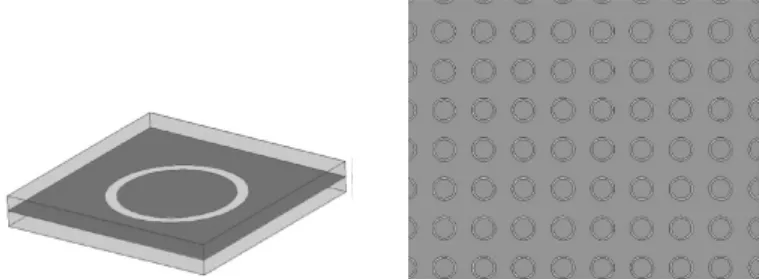
图1 圆环缝隙FSS结构图

图2 HFSS计算圆环缝隙FSS结果

3 各项参数对FSS电磁特性的影响分析

3.1 介质参数的影响

由于任何实际应用的FSS都需要介质作为支撑，所以介质对FSS电磁特性的影响是必须要考虑的。下面就从介质的介电常数、有无损耗、介质厚度三个影响因素进行分析。

3.1.1 介电常数的影响

圆环缝隙金属板两侧分别用相对介电常数为2.0和3.0的介质板（其他参数不变），与相对介电常数为1.0的情况进行对比，HFSS仿真结果如图3所示。介质的相对介电常数为2.0的情况下，FSS的谐振频率降低到10GHz附近，在相对介电常数为3.0的情况下，谐振频率更是降低到8GHz附近。

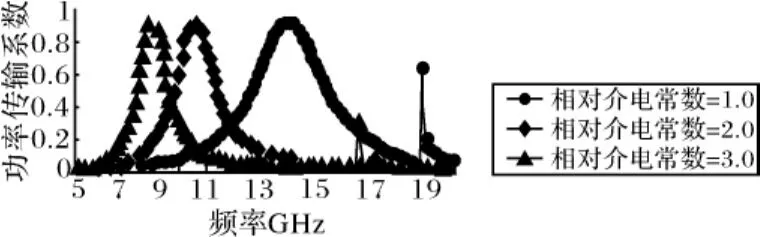
图3 不同介电常数的介质对FSS传输特性的影响对比

由仿真结果可以看出：在其他参数不变的前提下，介质基板的介电常数增大会使FSS的谐振频率显著降低。3.1.2 介质损耗的影响

采用相对介电常数为2.0的无耗介质的情况作为参考，分别用电损耗角正切值（tanδ）为0.01和0.03的两种有耗介质作为对比，其他参数均相同，结果如图4所示。

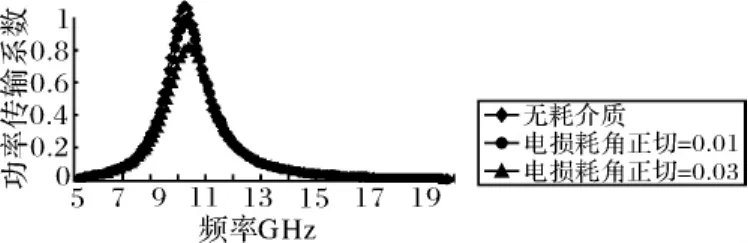
图4 不同电损耗角正切值的介质对FSS传输特性的影响对比

由计算结果看出：介质损耗会明显降低FSS的传输性能，同时微弱地改变FSS谐振频率。无耗介质在谐振频率处功率传输系数可以到1，电损耗角正切值为0.01的情况下，谐振时功率传输系数只能达到0.9，电损耗角正切值增大，功率传输系数下降明显。

3.1.3 介质厚度的影响

为了分析介质厚度对FSS传输特性的影响，下面分别计算了两侧介质厚度为2mm、3mm、4mm的情况，与1mm的情况作比较，其他参数不变，结果如图5所示。

从图中可以看出，介质厚度为1mm时，FSS谐振频率在9.7GHz，2mm 时降低到8.8GHz，3mm 时为8.7GHz，4mm时为8.6GHz。结果表明介质厚度增加会使谐振频率降低。

3.2 单元周期大小的影响

本文分别计算了单元周期为16mm＊16mm、14mm＊14mm、12mm＊12mm三种情况下FSS的传输特性（其他参数不变），结果如图6所示。

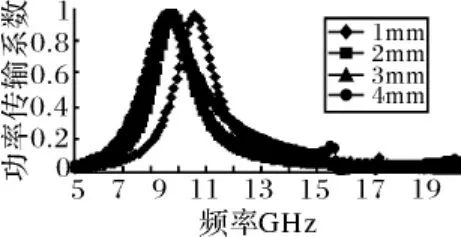
图5 不同厚度的介质对FSS传输特性的影响对比

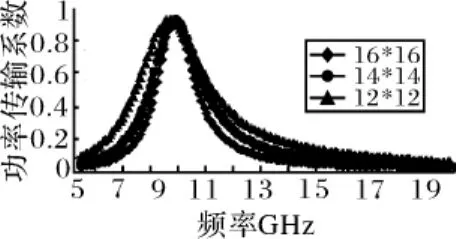
图6 不同单元周期对FSS传输特性的影响对比

HFSS仿真结果表明：单元周期主要影响FSS的带宽，单元间隔越大，带宽越窄。

3.3 圆环内径的影响

B.A.Munk教授指出环状单元的平均周长近似等于一个波长时产生谐振［1］。下面通过计算不同内圆环半径情况下FSS的传输特性来进行分析，结果如图7所示。

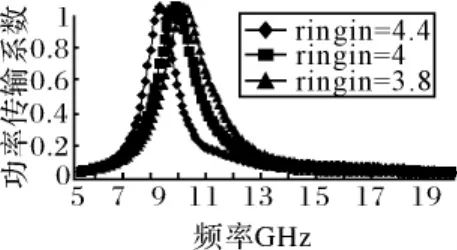
图7 不同圆环内径对FSS传输特性的影响对比

结果表明：在其他条件不变的情况下，降低内圆环半径会使谐振频率变高，实际上也就是通过改变圆环的平均周长改变了结构的谐振频率。该算例的仿真结果也正好验证了B.A.Munk教授的结论。

4 结语

本文利用HFSS仿真软件，对两侧有对称介质支撑的平面无限大单层圆环缝隙FSS阵列的传输特性进行了分析，可以得到如下结论：1）介质的介电常数增大会使FSS谐振频率显著降低；2）介质损耗会明显降低FSS的传输性能，同时微弱地改变FSS谐振频率；3）介质厚度增加会使谐振频率降低；4）单元周期主要影响FSS的带宽，单元间隔越大，带宽越窄；5）降低内圆环半径（平均周长）会使谐振频率变高。该结论直观、简明，对于关心FSS的工程技术人员具有重要的参考价值。

［1］B.A.Munk.Frequency Selective Surface：Theory and Design［M］.New York：John Wiley ＆Sons，Inc，2000：63-226.

［2］C.C.Chen.Transmission Through a Conducting Screen Perforated Periodically with Apertures［J］.IEEE Transactions on Microwave Theory and Techniques，1970，18（9）：627-632.

［3］C.C.Chen.Scattering by a Two-Dimensional Periodic Array of Conducting Plates［J］.IEEE Transactions on Antennas and Propagation，1970，18（5）：660-665.

［4］C.C.Chen.Diffraction of Electromagnetic Waves by a Conducting Screen Perforated Periodically with Holes［J］.IEEE Transactions on Microwave Theory and Techniques，1971，19（5）：475-481.

［5］C.C.Chen.Transmission of Microwave Through Perforated Flat Plates of Finite Thickness［J］.IEEE Transactions on Microwave Theory and Techniques，1973，21（1）：1-6.

［6］S.B.Savia and E.A.Parker.Equivalent circuit model for superdense linear dipole FSS［J］.IEE Proc.Microw.Antennas Propag，2003，150（1）：37-42.

［7］Kamal Sarabandi and Nader Behdad.A Frequency Selective Surface With Miniaturized Elements［J］.IEEE Transactions on Antennas and Propagation，2007，55（5）：1239-1245.

［8］M.D’Amore，V.De Santis and M.Feliziani.Magnetic Shielding of Apertures Loaded by Resistive Coating［J］.IEEE Trans.Magn.，2010，46（8）：3341-3344.

［9］M.D’Amore，V.De Santis and M.Feliziani.Equivalent Circuit Modeling of Frequency Selective Surfaces Based on Nanostructured Transparent Thin Films［J］.IEEE Transactions on Magnetics，2012，48（2）：703-706.

［10］谢拥军，刘莹，等.HFSS原理与工程应用［M］.北京：科学出版社，2009：268-281.

［11］李明洋.HFSS电磁仿真设计应用详解［M］.北京：人民邮电出版社，2010：1-2.