基于EDA的机会监听中继选择的改进机制

王 恒，纪 红，李 曦

(北京邮电大学泛网无线通信教育部重点实验室，北京 100876)

近年来，中继协作技术发展十分迅速。由于中继协同通信对于抵抗信道衰落和提升传输性能方面具备很强的优势。因此，吸引了越来越多的学者对其进行深入研究。文献［1］和文献［2］分别提出了基于最大合并比(MRC)的正交传输机制和应用分布空时码(DSTC)的协作传输机制。在文献［3］中，作者提出了一种机会中继选择机制，该机制利用简易的分布式算法得到了与应用分布空时码等高复杂度的中继机制一样的分集增益，被中继领域的研究人员广泛讨论。文献［4］在此基础上，进一步将确认和退避机制引入到机会中继选择机制中，减少了冲突带来的时延增加等问题。作为另一种改进方案，作者在文献［5］中提出了一种结合中继间监听和机会中继选择的机会监听中继选择机制。作者通过理论推导以及仿真实现证明该方案能够充分利用重传机制有效降低误包率。但是，文献［5］并没有考虑到监听信道对于系统的影响，同时，由于该机制中算法参数的简化，使得系统的适应性降低。

针对以上问题，本文提出了基于分布估计算法(Estimation of Distribution Algorithms，EDAs)的改进方案。在考虑到监听信道影响的同时，也给予了中继节点不断进行参数优化的学习功能。理论分析和仿真证明，该机制可以进一步提升系统的性能，并使得中继系统可以根据环境持续地做出改进。

1 基于中继间监听的机会中继

系统模型如图1所示，所考虑的无线通信系统有n个中继器R1，R2，…，Rn，其中第i个中继器Ri对应的与源节点的信道增益和与目的节点的信道增益分别为hS，i与hi，D，第i个中继器与第j个中继器之间的信道增益为hi，j。假设所有的中继设备工作在半双工模式下，同时各个节点间的前向信道和反向信道条件相同。场景处在一个缓慢变化的信道环境下(即数据重传时的信道增益变化可忽略不计)。

通过监听源节点与目的节点之间传输的RTS和CTS分组，中继节点可以获得自己与源节点和目的节点之间的信道增益，同时，通过监听各个中继参与源节点和目的节点的协同通信时发送的分组包，中继节点Ri也可以获得自身与其他中继节点Rj的中继间信道增益hi，j，其中，i，j={1，2，…，n}。

图1 基于中继间监听的机会中继系统模型

中继节点判定自己正确接收源节点发送的信息后(设正确接收源节点发送信息的中继数量为K1)，便可以参与竞争源节点与目的节点间的协同通信。该竞争机制是一种基于分布式计算的计时器机制。中继Ri对应的计时器初始值Ti为

式中:λ是一个以时间为单位的常数，因此Ti的大小完全由ai确定。各个中继分别根据自己采集到的信道增益启动自己的计时器进行倒计时，初始值Ti最小的中继节点将竞争到并参与进行源节点与目的节点的协同通信。在协同通信过程中，被选择进行协同通信的中继节点进行数据传输的同时，其他未正确接收源节点发送信息的中继节点(数量为n－K1)对其进行监听，并将监听到的数据与自己从源节点接收到的数据利用CC(simple Chase Combining)方式进行合并，这样，就会有中继节点通过监听机制带来的空间分集更正自己的错误信息。之前没有正确接收信息的中继节点可以重新利用CRC判定自己是否更正成功。设此时得到正确信息的中继节点为K2，则有K1≤K2≤n。这样做的好处在于:在协同通信时，当目的节点没有正确接收到数据后再进行中继节点的计时器竞争机制的时候，会有更多的中继节点参与竞争(K1≤K2)，这样，在重传的时候就会有更大的机会成功传送数据。

在原始的机会中继选择机制(无中继间监听机制)中，ai由以下两种方式得到:1)=(文献［5］在讨论原机会机制时默认的方式);2)ai(文献［6］使用的方式)。然而根据文献［5］的分析，各中继节点考虑的因素中，源节点到自身的信道增益对于协同增益的影响减弱了。该机制中，从中继节点发送到目的节点的信道增益是认真考虑的重点。在文献［5］中，定义中继间监听的机会中继机制中的中继节点Ri对应的ai为

由式(1)，(2)可知，在所有得到正确信息的中继节点中，自身到目的节点的信道增益最好的中继节点会优先竞争成为参与协同通信的节点。同时，不失一般性，将新转化为可参与竞争的K2－K1个中继标号为{K1+1，K1+2，…，K2}。由于信道环境是缓慢变化的，所以对于各个中继Ri的信道增益hi，D不变。因此，对于所有第一次参与竞争的中继来说，竞争的结果是不变的，只需要比较RK1+1，RK1+2，…，RK2中最小的定时器初始值与第一次成功参与协同通信的中继节点(设为RK)的定时器初始值。这样，在该机制中，数据重发时参与竞争的中继为 RK，RK1+1，RK1+2，…，RK2。

2 原机制的不足与改进的方案

2.1 问题描述

根据上面的讨论，通过中继间监听机制的引入使得数据传送的误包率降低，从而提升了信息传输的可靠性。然而，这种监听机制的引入将机会选择机制的优化范畴进行了一定的扩展，对于原机会中继机制的调整仅仅减少一个参量hS，j的考量是不够的。

例如这样的一个场景，如图2所示，目的节点与源节点之间有3个备选中继节点，设为R1，R2和R3。其中，表示信道条件的直线中，为实线的直线说明该条信道质量满足要求(即在该信道传输的数据可达)，为虚线的直线说明该信道质量不满足要求(即在该信道传输的数据不可达)。同时由图可见，从R2到Destination的信道由于建筑物或其他环境因素的干扰使得该信道质量非常不好，即满足。

图2 假设场景

按照在上一部分对于原监听机会中继机制的描述，可以得出:在成功接收源节点发送的中继R1和R2中，R1会在计时器竞争机制中胜出(因为)。而在协作通信中，很有可能Destination没有正确接收信息而要求重传。此时，只有R2能够正确监听到R1传送时的数据(从R1到R3的信道为虚线)，所以在第2次竞争中，仍然是R1与R2的竞争，排除其他因素，下一次参与协作通信的仍将是R1。可以发现:在假设场景中，协作通信的误包率将急剧增加。

此外，当场景环境的信道平均质量不佳时，重传的可能性将大大增加，因此应该更注重于选择一个能使更多中继监听到自己的中继节点。这样，类似于假设场景中的问题就可以很好地解决。

2.2 改进方案

2.2.1 分布估计算法

分布估计算法(Estimation of Distribution Algorithms，EDAs)是近些年来在进化计算领域兴起的一类新型算法，由于它在群体模型构建和演化的高适应性以及该算法的高收敛速度，使得它吸引了很多的研究人员的注意并迅速成为进化计算领域的研究热点，应用于多个方面的优化机制中。分布估计算法不同于传统的进化算法，它直接描述整个群体的进化趋势，取代了传统进化算法中对于个体的交叉变异操作，是统计学习理论与随机优化算法的结合。

作为快速发展的优化算法，分布估计算法不仅能够有效解决很多髙维非线性的优化问题，同时它对于进化算法提供了一个新的思路，使得该算法在科学研究和工程应用等领域有着很大的利用价值和发展前景。本文中，将利用它提出一个改进的中继选择方案。

2.2.2 改进的机会监听选择方案

在提出的改进方案中，仍以图1所示的模型作为中继选择改进机制的系统模型。在改进方案中假设，中继节点可以通过监听机制感知得到自身与其他中继节点间的信道增益hi，j，同时也可以通过目的节点发送的ACK，得到这次通信是否成功的信息(从而记录统计一次通信完成需要的重传次数)。本文提出的改进主要体现在两个方面:1)对于计时器初始值的计算增加了其他必要的参数;2)中继节点的竞争参量的确定加入了可以不断改善自身的学习特性。

原机会监听中继选择机制中，仅仅将|hi，D|2作为ai的计算方式是不够的。还应该考虑到其他的信道质量。因此，将原的计算方式扩展为

这样，计算ai值的时候，中继节点会考虑自身与其他中继节点的信道质量，可以让更多中继监听到自己的中继节点的竞争力，从而避免了类似于在假设场景中出现的现象。由于引入了更多的参数，因此，能否合理地确定这些参数的取值，以及这些数值的算法复杂度是否可以接受便成为了下一步要解决的问题。

为了解决这个问题，本文提出了基于分布估计算法的参数学习机制。选用属于分布估计算法之一的贝叶斯优化算法［7］，该算法具体步骤如下:1)以随机的形式产生各个个体，组成初始种群;2)按照一定的原则在种群中选择优势的个体;3)根据选择出来的个体构建符合要求的贝叶斯网络;4)利用贝叶斯网络的联合分布函数生成新的个体组成新的种群;5)将新的种群替换掉(部分)原种群，从而产生下一代种群;6)看算法终止条件是否满足，若满足，算法终止;若不满足，重新从第二步开始该算法。

在该算法中，贝叶斯网络内的连续型数据的实际意义往往无法明确，同时，也为使该算法的执行效率更高，因此将对应于每个中继Ri的计时器参数αi(j=1，2，…，i－1，i，i+1，…，n)，β 和 γ 进行离散化处理。将它们的取值范围变为从0到1最短步长为2－m的离散值。在上面的前提下，提出了具有学习特征的改进策略，针对于中继Ri，改进方案如下:

1)一次通信结束后，立即由概率模型(第一次则为全随机模型)生成对应于下一次通信的各个参数αi，β和γ准备参与下一次通信的计时器计算，从而最大限度地保证Ti的计算不受改进方案影响而降低效率。

2)在一次通信完成前(无论是否有重传或重传多少次)，αi，β和γ不会改变(避免影响学习能力)并且当通信结束时记录本次通信的αi，β和γ的取值以及本次通信的重传次数。

3)对通信次数进行记录，当通信次数达到N时，对所有记录的αi，β和γ，以其所对应的通信的重传次数为判定规则选取重传次数少的N1组αi，β和γ作为优势个体组成新种群，并依据该种群构建贝叶斯网络，然后将通信次数归零，同时对每次通信的参数αi，β和γ记录清零。构建的贝叶斯网络的联合分布函数替换原概率模型作为生成αi，β和γ的新概率模型。

此方案的好处在于，它考虑到了其他信道质量对于协同通信可能产生的影响，并且当环境更符合原机会监听机制的计算方法时，提出的方案仍可通过学习产生一样的结果(αj=β=0，γ=1)，同时它的不断自我优化的特性，使该中继通信系统的性能不断改善，达到较小的重传次数期望值和误包率。

3 仿真结果

为了进一步验证本文提出的基于分布估计算法的改进方案的优势，采用蒙特卡洛方法对改进的方案和原机制进行仿真与比较。利用工具Matlab和Mathematics，从误包率和重传次数两方面对其进行仿真实现。在仿真过程中，选取 n=3，m=6，N=50。

图3给出了本文提出的新的机会监听机制与原监听机制和机会选择机制的误包率比较，通过16QAM和QPSK两种调制方式的仿真实现，可以看到，本文提出的新方案对于误包率的减小有着很好的改善。能够更加充分地利用监听机制所具有的提升数据传输成功率的性能。

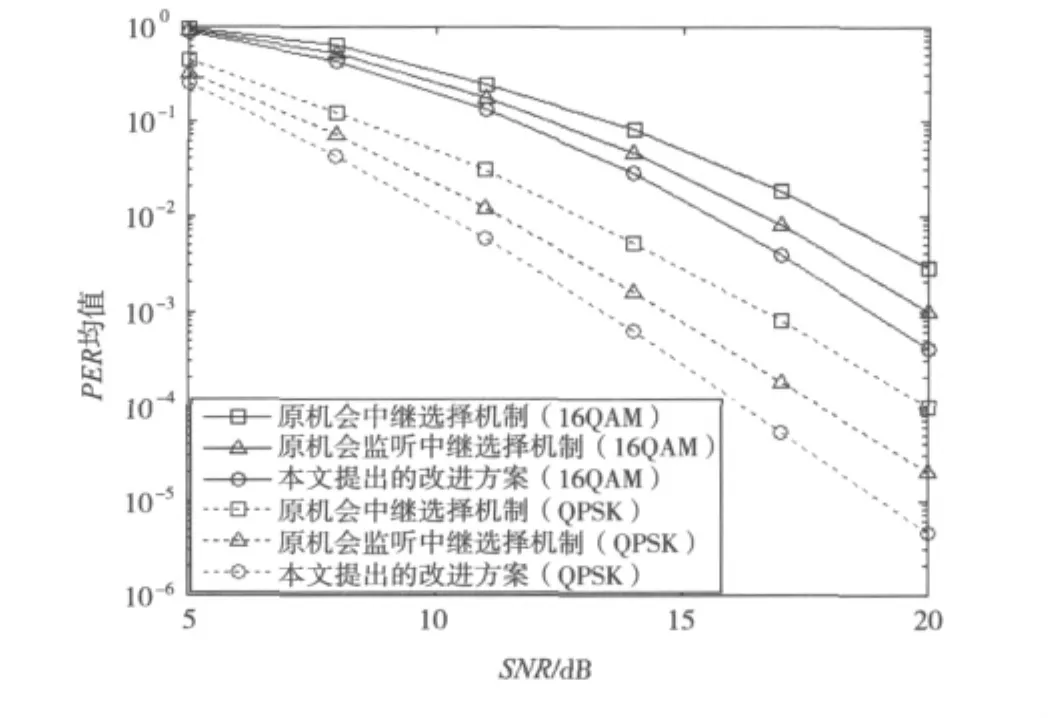
图3 本文的改进机制与原机制的误包率比较

在信道质量很差的条件下，各个中继机制的重传期望随时间变化的直方图如图4所示。通过图4可以发现，本文提出的改进方案有着自我改善的学习性能，通过不断的以N为周期的学习，新方案使得中继节点可以根据统计数据对自身参数进行优化，从而改善整个系统的传送效率，使传输的有效性得以提升。该方案可以不断适应环境变化并提升整个系统的通信性能。通过EDA算法以及相对应的新机制的引入，不仅可以使中继在优化参数取值的能力上得到提升，同时也使得中继节点具备了一定的自适应能力。

4 小结

本文在原机会监听中继选择机制的基础上，通过分布估计算法的引入提出了一个更适于在中继间监听机制中执行的方案。通过理论分析表明，利用分布估计算法的高收敛性和对于解决非线性、变量耦合等优化问题的优势，本文提出的方案不仅可以帮助中继节点根据环境具体情况在统计意义上选择出更适应的计算参数，以实现整体性能的优化，提高整个系统通信的可靠性，同时还使得整个中继系统具备了一定的自适应学习能力。仿真结果显示，该方案使得各个中继节点经过周期性的学习，可以不断改进自身的参数，使得系统的整体机制持续地自我改善。

图4 新的改进机制自我改善的学习性能比较

［1］ SENDONARIS A，ERKIP E，AAZHANG B.User cooperative diversitypart ii:implementation aspects and performance analysis［J］.IEEE Transactions on Communications，2003，51(11):1939－1948.

［2］ LANEMAN J N，WORNELL G W.Distributed space－time－coded protocols for exploiting cooperative diversity in wireless networks［J］.IEEE Trans.Information Theory，2003，49(10):2415－2425.

［3］ BLETSAS A，KHISTI A，REED D，et al.A simple cooperative diversity method based on network path selection［J］.IEEE Journal on Selected Areas in Communications，2006，24(3):659－672.

［4］刘丹谱，郝建军，乐光新.用于机会中继的一种最佳中继选择算法［J］.中国电子科学研究院学报，2008，3(5):483－487.

［5］ LYNN N，TAKYU O，ADACHI K，et al.Cooperative ARQ using distributed relay selection and inter－relay opportunistic listening［C］//Proc.IEEE 21st International Symposium on PIMRC Workshops.Istanbul，Turkey:IEEE Press，2010:467－472.

［6］ BLETSAS A，LIPPMAN A，REED D P.A simple distributed method for relay selection in cooperative diversity wireless networks based on reciprocity and channel measurements［C］//Proc.61st IEEE Semiannu.Vech. Technol. Conf. Stockholm， Sweden:IEEE Press，2005:1484－1488.

［7］ HAUSCHILD M，PELIKAN M，SASTRY K，et al.Analyzing probabilistic models in hierarchical BOA［J］.IEEE Trans.Evolutionary Computation，2009，13(6):1199－1217.