重载车辆-简支梁桥耦合振动影响参数分析
2012-06-05蒋培文贺拴海宋一凡王凌波周勇军
蒋培文, 贺拴海, 宋一凡, 王凌波, 周勇军
(长安大学 公路学院,陕西 西安 710064)
近年来,众多国内学者对车桥耦合振动问题试图运用数值方法进行求解,文献[1]将车与桥相互作用作为整体建立体系振动微分方程组,应用数值分析方法求解了公路简支梁、连续梁桥动力响应;文献[2-3]应用达朗伯原理建立简支梁桥车桥耦合振动分析模型,应用数值分析方法求解微分方程组;文献[4]运用Newmark逐步积分法解得匀变速移动质量与简支梁耦合系统的响应;文献[5]采用单个移动质量-弹簧-阻尼模型模拟车辆,应用达朗贝尔原理和位移协调条件,推导出车桥耦合振动的运动方程;文献[6]以接触力学为基础,运用了泰勒级数及小变形理论的假设,推导了轮轨接触几何关系;文献[7]根据势能驻值原理及形成结构矩阵的“对号入座法则”,导出车桥系统的空间振动矩阵方程;文献[8]研究了大跨度悬索桥的车桥耦合振动。
车桥耦合振动的研究仍存在许多尚未解决的技术难题[9-10],简支梁桥作为所有桥型中最常见的一种,在公路交通中得到了相当广泛的应用。对于简支梁桥的车桥耦合振动也有不少的研究成果,但总结起来存在以下几点不足:① 车辆匀速过桥的耦合振动研究成果较多,变速过桥耦合振动的成果较少;② 随机路面不平整度对耦合振动的影响研究成果较多,路面局部病害及病害位置对耦合振动的影响研究成果较少;③ 绝大多数研究文献仅通过单因素的变化计算少量数据点拟合曲线来研究参数的影响。
1 分析方法及算例验证
1.1 分析方法
本文方法利用大型通用程序ANSYS的强大功能,结合APDL语言对公路桥梁各种复杂行驶工况下的车桥耦合振动响应问题进行较精确的数值分析[11-15]。
1.1.1 ANSYS模型的建立
(1)桥梁模型的建立。ANSYS在桥梁的建模分析方面有着极其广泛的应用,具有丰富的单元库及材料库,可以对任何结构形式的桥梁进行全桥仿真分析。
(2)车辆模型的建立。本文方法将车辆模型与桥梁模型建立于同一个ANSYS工作环境下,但两者之间无任何直接联系,各自独立,两者间耦合作用关系通过APDL编程语言计算并将其在任意时刻施加于车辆及桥梁结构。在ANSYS环境下,利用MASS21、COMBIN14、BEAM4等单元即可对各种车辆模型进行建模分析。在此以平面双轴车辆为例,车辆模型及参数示意图如图1所示。
图1中,Mc为车体质量;Ic为车体质心绕z轴转动惯矩;Mi(i=1,2)分别为第i个轮对质量参数;Kui和Cui(i=1,2)分别为一系弹簧阻尼器的刚度及阻尼;Kdi和Cdi(i=1,2)分别为二系弹簧阻尼器的刚度及阻尼;b1、b2分别为车体质心距后轴、前轴的距离;c1为驾驶员位置处距前轴的距离。
由于本文方法建模时桥梁模型与车辆模型之间均相互独立,当N辆车以不同行驶参数作用于桥梁时,可在ANSYS环境下建立N个相互独立的车辆模型,以进行多车辆过桥时的耦合振动分析。

图1 1/2车辆模型示意图
1.1.2 确定车辆各轮在任意时刻的坐标
桥面车辆的行驶状态通常为匀速或匀变速的直线行驶状态,本文采用车辆行驶起始节点P(其空间三维坐标分别为Px、Py、Pz)与车辆行驶结束节点Q(其空间三维坐标分别为Qx、Qy、Qz)来定义车辆的行驶方向,结合车辆的初始速度v0、车辆的加速度a、车辆的行驶时间t,即可确定车辆模型中各轮位置坐标。
以图1所示的平面双轴车为例,各轮位置坐标计算结果为:

1.1.3 竖向荷载与挠度的转换
车辆在任意时刻t的各轮坐标确定之后,由于该坐标点未必处于桥梁节点处,故存在车轮位置处与桥梁节点处竖向荷载与挠度的转换问题。
(1)与车轮位置最近处节点的等效荷载。如图2所示,梁单元等效荷载转换可通过(2)式梁单元的荷载等效原理[16]进行计算,转换结果见(3)式,其中,a、b为荷载P距梁端A、B的距离;L为梁端A、B间距离;RA、RB、MA、MB分别为荷载P在梁端A、B的等效竖向力及弯矩;We为单元外力功;¯p(x)为荷载密度函数;v(x)为位移函数;N(x)为单元形状函数矩阵;qe为节点位移列阵。

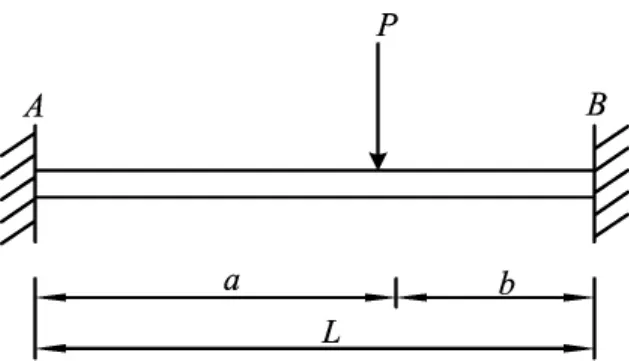
图2 梁单元的等效荷载转换示意图
(2)车轮位置处的竖向位移插值函数。如图3所示,根据文献[16]推导结果,纯弯梁单元的位移场(竖向挠度)为:

此外,扭矩的荷载及位移转化可根据线性规律进行计算[15],不再赘述。

图3 梁单元位移转化示意图
1.1.4 车桥耦合相互作用的数值计算方法
以图1所示的平面双轴车辆为例,该模型包含4个独立的自由度,为计算简便,假定4个独立自由度分别为轮对处竖向位移自由度z1、z2与支承车体点的竖向位移自由度z′1、z′2。根据力的平衡原理或虚位移原理,可推得该车辆的振动方程为:
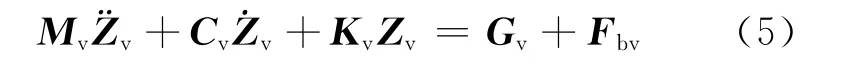
其中,Mv、Kv、Cv分别为车辆质量矩阵、刚度矩阵和阻尼矩阵,即

其他参数均为重力荷载及耦合荷载向量,且

由以上计算结果可以看出Mv、Cv、Kv、Gv均为常量,仅与车辆的初始参数有关,而不随时间及车辆位置而变化,仅有Fbv随时间及车辆位置变化。故本文方法将车辆模型直接建立于ANSYS环境下,将Fbv通过APDL语言在车辆行驶过程中实时计算,并结合Gv以外力形式将(5)式右边项施加于车辆模型中各自由度所在节点,进而直接调用ANSYS的时程分析模块进行各子步的时程分析。假定车轮下部与桥面在任意时刻紧密接触,当任意时刻的车轮节点的位移、速度,及与车轮接触桥梁位置的位移、速度、不平整度数据确定后,通过(6)式可求解车辆在任意时刻与桥梁间的接触力F(t),从而计算车辆过桥的时程响应。

其中,DC(t)为t时刻车轮节点的竖向位移;DQ(t)为t时刻车轮正下方对应桥梁节点的竖向位移;VC(t)为t时刻车轮节点的竖向速度;VQ(t)为t时刻车轮正下方对应桥梁节点的竖向速度;W为车轮所在处的路面不平整度数据;K为车轮与桥梁连接弹簧的刚度;C为车轮与桥梁连接弹簧的阻尼。
节点速度VC(t)、VQ(t)可通过数值微分相关理论,调用位移计算结果数据,采用如下一阶二点数值微分近似公式或一阶三点数值微分近似公式进行计算,即

结合以上分析,将车辆过桥总过程划分为较密的若干个子步,各子步作用时间为Δt。当0时刻车辆到达桥头支点时,车辆的行驶状态可根据需要赋于相应数值,车桥接触点的竖向位移为0;第1个Δt过后,由于Δt很小,假定车辆的各自由度状态不发生变化,但位置随Δt产生了微小变化,根据变化后的车辆位置结合未变化的自由度状态可得到Δt时刻车桥接触点的竖向位移。在此之后,根据t-Δt时刻及t时刻车辆自由度状态及车桥接触点竖向位移,即可推算出t+Δt时刻的相关参数,递推直到车辆下桥为止。

图4 本文方法分析结果
1.2 1/2车辆模型算例分析
本算例采用车辆和简支梁的技术参数按照文献[3]取值,本文方法计算结果如图4所示,文献[3]结果如图5所示,可见两者吻合良好。
洙赵新河干流西起菏泽市东明县宋砦村,向东流经东明县、牡丹区、郓城县、巨野县和济宁市嘉祥县、市中区等6个县区,于刘官屯村入南阳湖,全长145.05 km,其中菏泽境内长106.53 km。菏泽市洙赵新河有邱公岔、郓巨河、巨龙河、洙水河、鄄郓河、太平溜、赵王河、徐河等一级支流。

图5 文献[3]分析结果
2 重载车辆变速过桥响应分析
本节根据已验证的方法,研究当重载车辆的上桥速度、出桥速度变化时,车辆匀变速行驶过桥时的车桥耦合振动响应。车辆参数见表1所列,简支梁跨径为30m;单位长度质量为6.732×103kg/m;抗弯刚度为1.646×1010N·m2,上桥速度、出桥速度取常见的20~120km/h,间距5km/h,并进行排列组合,共21×21=441个工况。
运用ANSYS的APDL语言进行批处理运算,将计算结果绘制成三维变化图,如图6~图8所示。

表1 车辆参数

图6 跨中截面冲击系数变化

图7 车辆竖向加速度峰值变化

图8 跨中截面竖向加速度峰值变化
由图6~图8可以发现以下规律:
(1)挠度冲击系数变化曲面较为平滑,其数值不随上桥、出桥速度的增加而单调增加,呈现出明显的起伏状,且起伏较大;上桥、下桥的速度都对挠度冲击系数有着明显的影响,且上桥速度的影响偏大。
(2)弯矩冲击系数变化曲面与挠度冲击系数变化曲面相比凹凸不平,其数值不随上桥、出桥速度的增加而单调增加,呈现起伏状,但起伏较小。上桥、下桥的速度都对弯矩冲击系数有着明显的影响,且上桥速度的影响偏大。
(3)车辆的最大、最小竖向加速度曲面均较为平滑,而且与冲击系数变化不同,随着车速的增加,车辆最大、最小竖向加速度基本单调递增,仅有少量的起伏;相同上桥、下桥速度时的车辆竖向加速度最大、最小值的绝对值比较接近。
(4)桥梁控制截面最大、最小竖向加速度曲面十分凹凸不平,波动很大,有随车速增大而增大的趋势,但规律很不明显。其数值大于车辆的竖向振动峰值,即当车辆过桥时,桥上行人的舒适性一般情况下低于车内驾驶员的舒适性。
3 桥面局部凹陷响应分析
本节根据已验证的方法,研究当重载车辆的行驶速度、桥面局部凹陷位置变化时,车辆匀速行驶过桥时的车桥耦合振动响应。车辆参数见表1所列,简支梁参数如前文所述,凹陷大样如图9所示,车辆行驶速度取常见的20~120km/h,间距5km/h;桥面凹陷位置(凹陷中心距桥头距离)取1~29m,间距1m,并进行排列组合,共21×29=609个工况。运用ANSYS的APDL语言进行批处理运算,将计算结果绘制成三维变化图如图10~图12所示。

图9 凹陷大样示意
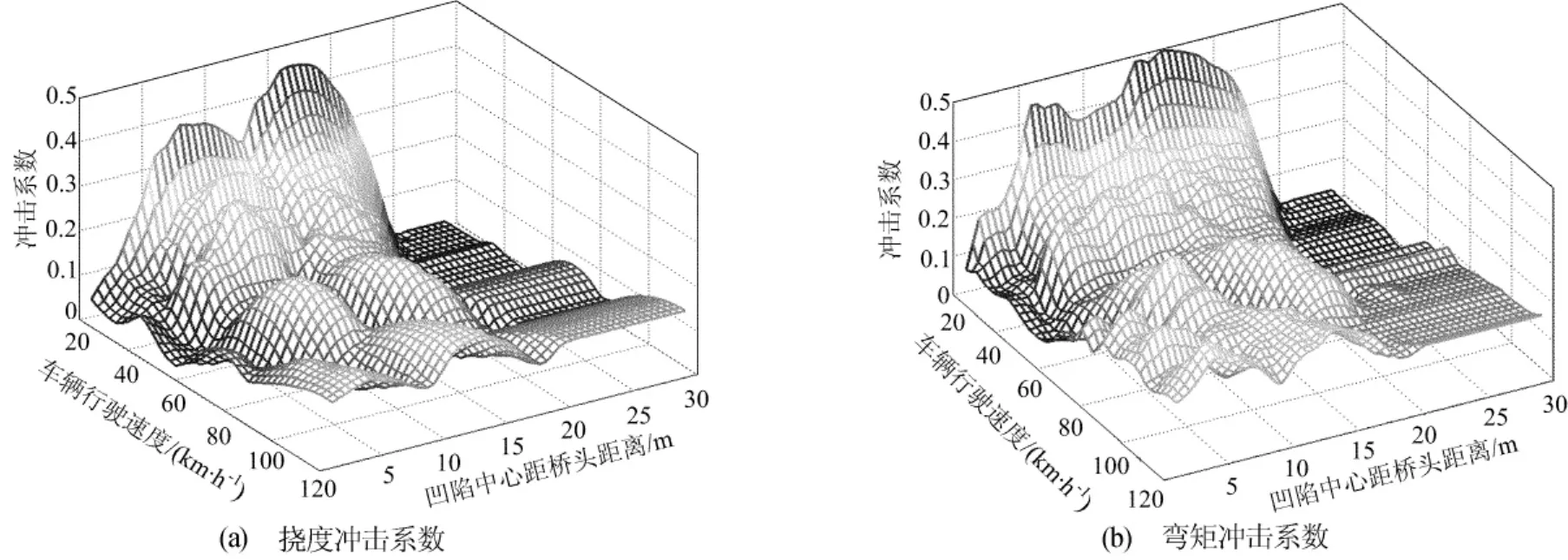
图10 跨中截面冲击系数变化
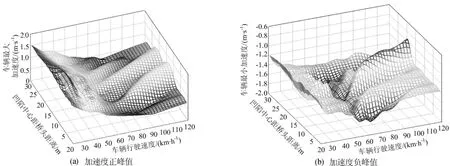
图11 车辆竖向加速度峰值变化

图12 跨中截面竖向加速度峰值变化
由图10~图12可以发现以下规律:
(1)挠度冲击系数变化曲面较为平滑,当凹陷出现在距桥头L/6~2L/3(L为跨径)时对控制截面的冲击系数有着明显的影响,反之则影响不大;与平整路面不同,车辆低速通过局部凹陷的桥梁时容易产生较高的挠度冲击系数。
(2)弯矩冲击系数变化曲面除较凹凸不平外与挠度冲击系数变化曲面变化规律类似。
(3)当凹陷出现在距桥头L/3~2L/3(L为跨径)时,对车辆的最大、最小竖向振动加速度有着明显的影响,反之则影响不大;车辆中速行驶会产生较不利的最小竖向加速度,但最大竖向加速度较小,低速、高速行驶则结论相反。
(4)桥梁控制截面最大、最小竖向加速度曲面凹凸不平,波动很大,随着凹陷位置的变化,曲面呈现3个明显的波峰,对应的凹陷位置约为L/6、L/2、5L/6(L为跨径)。曲面峰值数值大于车辆的竖向振动峰值,即当车辆过桥时,桥上行人的舒适性一般情况下低于车内驾驶员的舒适性。
4 结论
(1)当桥面平整时,减速过桥会产生较低的冲击系数。通过计算发现,一般情况下,上桥前减速、上桥后在桥面上减速以及不减速3种情况产生的冲击系数依次升高。
(2)当桥面在距桥头L/6~2L/3(L为跨径)处出现凹陷病害时,车辆即使低速通过也会产生很大的冲击系数,故出现此情况应当给予足够重视,尽快进行路面维修。
(3)当车辆高速过桥时会使车辆及桥梁控制截面产生较大的竖向振动加速度,后者的数值更大,因此桥面行人可能会感到较强的不适。
[1]王元丰,许士杰.桥梁在车辆作用下空间动力响应的研究[J].中国公路学报,2000,13(4):38-41.
[2]肖新标,沈火明.移动荷载作用下桥梁的系统仿真[J].振动与冲击,2005,24(1):121-123.
[3]沈火明,肖新标.求解车桥耦合振动问题的一种数值方法[J].西南交通大学学报,2003,38(6):658-662.
[4]彭 献,殷新锋,方 志.变速车辆与桥梁的耦合振动及其TMD控制[J].湖南大学学报:自然科学版,2006,26(5):19-21,37.
[5]丁南宏,林丽霞,钱永久,等.双链式悬索桥车桥耦合振动研究[J].兰州交通大学学报,2010,29(1):95-99.
[6]王雨权,林鸿洸.高速铁路车桥耦合轮轨接触几何关系与接触力的理论推导[J].科学技术与工程,2010(6):1449-1452,1457.
[7]李 波,郭占元.考虑温度影响的上承式钢管混凝土拱桥列车走行性研究[J].中国西部科技,2010,9(5),11-13.
[8]逄焕平,王建国,钱 锋.大跨度悬索桥的车桥耦合振动分析[J].合肥工业大学学报:自然科学版,2011,34(1):114-118.
[9]陈榕峰.公路桥梁车桥耦合主要影响因素仿真分析方法研究[D].西安:长安大学,2007.
[10]宋一凡.公路桥梁动力学[M].北京:人民交通出版社,2000:74-102.
[11]张 雄,王天舒.计算动力学[M].北京:清华大学出版社,2007:65-84.
[12]王新敏.ANSYS工程结构数值分析[M].北京:人民交通出版社,2007:499-550.
[13]邓凡平.ANSYS10.0有限元分析自学手册[M].北京:人民邮电出版社,2007:110-194.
[14]博弈创作室.APDL参数化有限元分析技术及其应用实例[M].北京:水利水电出版社,2004:59-97.
[15]曹雪琴.桥梁结构动力分析[M].北京:中国铁道出版社,1987:79-93.
[16]曾 攀.有限元分析及应用[M].北京:清华大学出版社,2006:46-88.
