杂波谱中心频率的估计方法研究
2012-06-05高一栋
高一栋 张 艳 牟 聪
(西安电子工程研究所 西安 710100)
1 引言
机载雷达作为一种平台运动雷达,为了提高对杂波的抑制而必须对平台运动效应做有效的补偿,需要对杂波的多普勒频率进行精确的估计[1]。本文首先介绍了杂波谱中心频率的理论计算方法,然后给出了两种基于原始回波的估计算法,并比较了这两种方法的优劣性,最后根据某机载雷达的回波数据对算法予以验证。
2 杂波谱中心频率的理论计算
图1为机载雷达对地工作示意图,设载机速度为V,波束指向的方位角为θ,俯仰角为Φ,方位波束宽度为θB,俯仰波束宽度为Δφ,载机高度为h,那么杂波的多普勒中心频率为[2]:


图1 雷达对地工作示意图
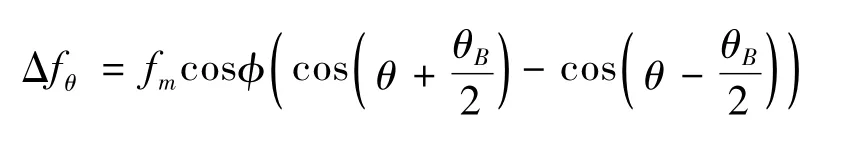
当方位波束宽度比较窄时,上式为:

雷达俯仰波束宽度引入的主杂波宽度为:
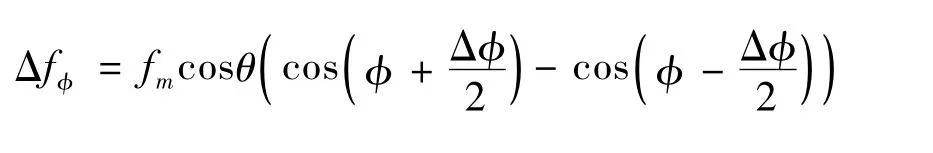
当俯仰波束宽度比较窄时,上式为:

由此可以得到杂波谱3dB带宽为:
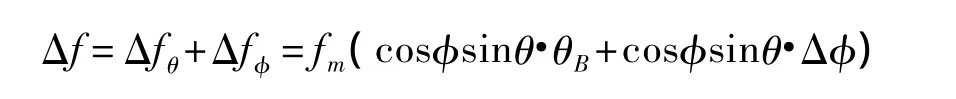
根据以上公式,如果在飞行中能实时的得到载机的速度,雷达波束的方位、俯仰角度,就可以比较准确的计算出杂波谱中心和3dB谱宽。
在实际应用中,虽然可以得到很精确的波束方位和俯仰角度值,但是由于载机扰动,它的速度、航向、横滚、纵摇是由惯导系统提供的,在匀速直线运动中,惯导提供的载机信息较为准确,但在飞机加、减速以及航向改变的情况下,惯导的速率有较大的延迟,这时候使用惯导数据对谱估计就会产生较大的误差,就需要考虑其它的方法了。下面介绍两种估计算法。
3 两种谱中心估计方法
目前采用的方法是质量中心法,这是一种依赖惯导的算法。理论上是以惯导信息为依据,通过幅度加权平均估计出比较精确的主杂波位置。首先,利用机载惯导系统所提供的参数(载机速度V,雷达天线方位角θ,俯仰角φ),粗略计算出杂波谱中心多普谱频率dc和3dB谱宽Δdc,则可以认为杂波谱的主要能量分布在[(dc-nΔdc-fe),(dc+nΔdc+fe)]范围内,其中fe为dc的最大估计误差。设dc所对应的多普勒通道号为M,nΔdc+fe所占的通道数为L,则杂波总能量为:
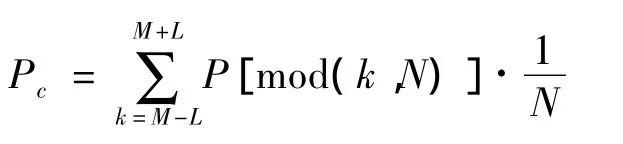
因此,可以得到归一化的杂波谱中心多普勒频率fdc和均方根带宽B的计算公式:

这种方法好处是计算量比较小,缺点是依赖于惯导,在飞机在非匀速直线运动时谱估计可能会出现较大的偏差。
如果不想依赖惯导,为了准确的估计杂波谱中心,那么需要对原始回波的频率进行分析,从而锁定主杂波位置,对于输入数据:
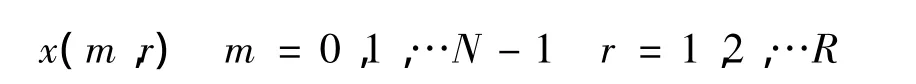
其功率谱为:
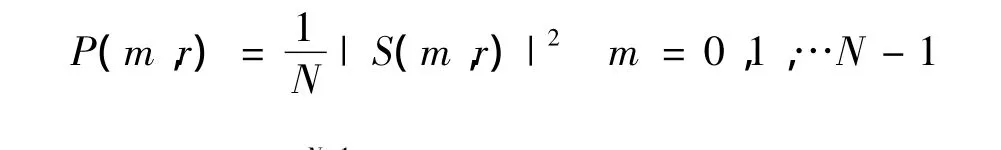

表1 距离单元—多普勒通道排列表
采用熵谱估计法,是一种运算量较大的估计法。因为主杂波的能量远高于噪声,对杂波谱功率近似逼近,对同一多普勒通道整个距离单元的能量加权,然后寻找能量最集中的多普勒通道就为主杂波位置。

m表示多普勒通道;r表示距离单元,取A(m)最大值;I表示能量最高的多普勒通道;A表示该普勒通道所有距离单元能量之和。I就为主杂波通道。
采用熵谱估计法的好处是算法简单,通过简单的求和就能得到主杂波位置。但是当出现个别强目标,它的反射能量高于主杂波,那么使用上面的办法估计出杂波谱中心就可能会出现偏差。
解决的办法是采用改进的熵谱估计方法,可以很好的避免这个问题。改进的熵谱估计法,就是使用概率统计的方法,首先在每个距离找出能量最高的多普勒通道:

Ir表示在距离单元r上能量最高的多普勒通道,对Ir进行统计,出现概率最高多普勒通道号即为主杂波中心位置。
4 试验数据结果分析
据为例进行验证。图2为雷达对地工作的某个cpi回波数据(纵轴表示幅度,横轴表示距离单元),积累脉冲个数为32点,飞机速度为44 m/s,方位角度:-33.8°,俯仰角度:-1.1°。图3为全距离段脉压结果图,图4为MTD后的叠加图。

图4MTD后的叠加(x:多普勒,y:幅度)
现在以某机载毫米波脉冲多普勒雷达的回波数

根据惯导提供的飞机速度,以及本CPI时刻的雷达方位角和俯仰角,采用质量中心法估计杂波谱中心,求出fd=5807Hz,将fd在频域补偿结果如图5所示。

图5 质量中心法补偿效果图
采用改进的熵谱估计法,得到Ir分布如表2所示,第1、3行表示多普勒通道,第2、4行表示该多普勒通道幅度出现最大的次数,很显然,杂波主要集中在第24和第25通道,第25通道幅度最强,另外第14通道出现最大幅度次数也较多,很可能是动目标引起,这张表格的统计和图4的波形很吻合。

表2 多普勒通道——最大幅度出现次数统计表
系统设计的PRF为最大不模糊速度对应的多普勒频率,方位扫描范围为载机飞行方向左右一定区域,因此地杂波多普勒频率在0~PRF之间,也就是杂波谱中心将会落在在0~PRF之内。那么取幅度出现概率最大的多普勒通道号25作为谱中心,重新计算fd:
fd=(25/32)×PRF=5483Hz重新进行杂波补偿,经过频谱搬移后,杂波效果如图6所示,补偿效果相对于图5,明显有了改善。

图6 改进的熵谱估计法补偿效果图
5 结论
综上所述,上述两种方法的实质都是先采用FFT的方法将时域数据变换到频域,然后在频域上直接对谱中心和谱宽进行估计。通过图5和图6的比较,可以说明使用质量中心法,在惯导数据不是很精确的情况下,运动的补偿效果还是会出现偏差的。熵谱估计法效果更好一些,但是更依赖于较强的地杂波。实际试验也证明了,在机载下视情况下,非均匀杂波背景适合用熵谱估计法,而车载雷达,地杂波较弱,适合采用质量中心法。
[1]George W.Stimson.机载雷达导论[M].北京:电子工业出版社,2005.
[2]黄勇,彭应宁等.基于频域处理的机载雷达自适应杂波抑制方法[J].系统工程与电子技术,2000,22(12):4 ~6.
[3]葛凤翔,孟华东等.杂波谱中心和谱宽估计方法[J].清华大学学报(自然科学版),2001,41(1):33~36.
