基于改进阈值函数和自适应阈值的小波去噪方法
2012-06-01左东广
周 帅,左东广
(第二炮兵工程大学 1系,陕西西安 710025)
近年来由于小波理论的不断发展,小波的应用也越来越广泛。小波分析方法是近年来发展起来的一种多分辨分析工具,目前已成功应用于信号处理等工程领域。在信号处理中,利用小波变换给信号去噪同样受到了许多学者的重视。在对小波去噪方法的研究中,出现了许多不同的基于小波变换的信号去噪方法,其中小波阈值去噪方法得到越来越广泛的应用[1]。
1 小波去噪原理
小波变换是一种重要的时频描述方法,具有较好的时频局部化性能。由小波变换理论可知其具备以下特点[2]:
(1)时频局部化。即小外波变换可定位出信号发生突变的时间和位置。
(2)多分辨率。即小波变换可以在不同尺度上刻画信号的局部性能,如边缘和断点等。
(3)选基灵活性。即小波变换可以根据信号本身的特点,选择适当的小波基函数,以便更好地逼近原始信号。
(4)去相关性。信号经小波变换后可以使大部分能量集中在少数几个小波系数上。
与传统的去噪理论相比,小波变换的时频局部化和多分辨率性能够在去除信号噪声的同时,较好地保留信号的突变部分或图像的边缘和纹理信息。随着小波分析理论的逐渐成熟,其应用领域也越来越广泛。小波信号去噪的本质在于根据信号和噪声变换后的系数在不同尺度上具有不同性质这一原理,采用适当的数学方法对含噪信号的小波系数进行处理,其实质在于减少或去掉有噪声产生系数的同时,最大限度地保留信号产生的系数,最后根据小波的性质,把经过处理的小波系数重构以得到去噪后的信号。从数学角度看,信号的小波去噪是一个函数逼近问题,即是如何在由母函数平移和伸缩展开的函数空间中,根据一定衡量准则,寻找对原始信号的最真实的逼近,从而实现原始信号和噪声信号的区分,达到信号去噪的目的。从信号处理角度来看,小波去噪是一个信号低通滤波的问题。因此,小波去噪可以看成低通滤波和特征提取的结合[2-4]。
2 小波阈值去噪的一般步骤
一个含噪的一维信号的模型可以表示成
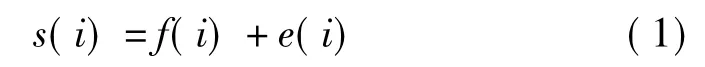
其中,f(i)是真实信号;e(i)是噪声信号;s(i)是含噪信号,i=0,1,…,n-1。
在实际工程中,有用信号通常表现为低频信号或者一些比较平稳的信号,而噪声信号通常表现为高频信号。去噪过程可以按以下方法处理:首先对信号进行小波分解,以3层为例,如图1所示,那么噪声通常包含在cd1,cd2和cd3中,接着对分解后的小波系数进行阈值处理,利用处理后的小波系数重构信号,这样就达到了去噪的目的。
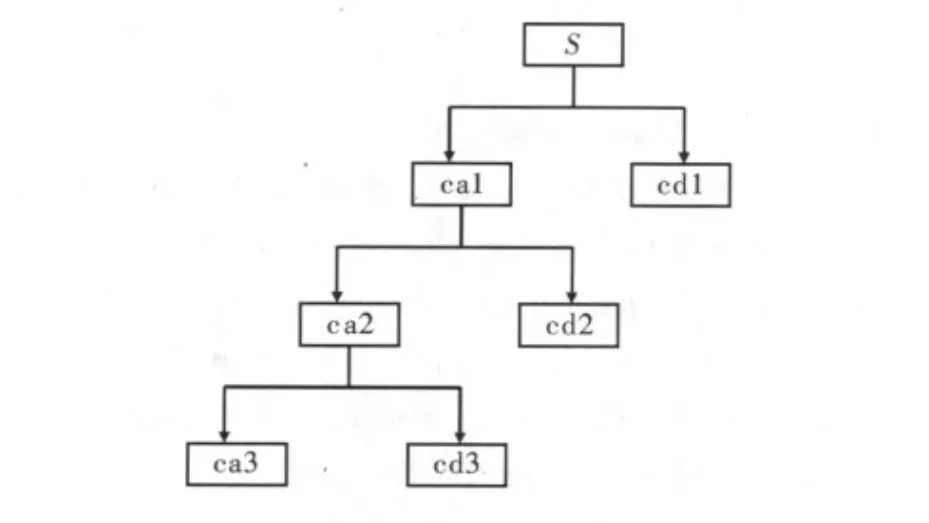
图1 三层小波分解结构图
由上可得具体的阈值去噪步骤为[5]:
(1)对带噪声的语音信号进行小波变换,得到不同尺度上的子波信号,将有用信号和噪声分开。这过程中涉及以下几个重要部分:
1)确定小波基及其阶数。小波基的阶数不同,则表现信号局部特点的能力也不同。一般情况下,阶数越高越能很好地表征信号局部特点,但计算量也会相应变大,当阶数>5阶时,小波基阶数的提高对提高表征信号能力的影响较小,因此一般选取阶数约为5~8。
2)确定小波变换的次数。当信号中白噪声的含量较多时,小波变换尺度要大一些,即小波变换次数要多一些,但相应地会增大计算量;相反的当信号中含噪声较少时,小波变换的尺度即变换次数可以少些,计算量也会相应的减少。
3)小波变换。通过选取合适的小波变换参数进行小波变换,就可得到不同尺度上的小波信号。
(2)确定各层小波信号的去噪阈值门限。
(3)选取阈值函数。
(4)小波逆变换。进行小波逆变换将经过阈值处理的小波系数进行信号重构,得到恢复的原始信号的估计值。
在上述的阈值去噪步骤中,合适的小波基、小波分解层数、阈值以及阈值函数直接影响去噪效果,其中阈值和阈值函数的选取至关重要。
3 小波阈值函数
3.1 传统的阈值函数
Donoho提出基于小波阈值的去噪方法,该算法在最小均方差意义下可以达到近似最优。根据其算法可以得出对小波系数处理的软、硬阈值函数。
硬阈值函数为

将小波分解后的系数的绝对值与阈值λ进行比较,小于阈值的点变为0,大于或等于阈值的点保持原值。在硬阈值处理过程中,由于硬阈值函数在整个小波区域内是不连续的,在λ和-λ处存在间断点,因此得到的估计小波系数值连续性差,可能引起重构信号的振荡。
软阈值函数为

软阈值方法处理后,小波系数值虽然连续性好,不存在间断点问题,易于处理,但由于当小波系数较大时,得到的估计小波系数值与原来的小波系数值有固定的偏差,也会给重构信号带来不可避免的误差[6]。此外,软阈值对大于阈值的小波系数采取恒定值压缩,这与噪声分量随着小波系数增大而逐渐减小的趋势不相符。
在式(2)和式(3)中,wj,k表示信号分解的小波系数;j,k表示阈值方法得到的小波系数估计值;λ为阈值

其中,σ为噪声标准差,可以用以下经验公式进行估计
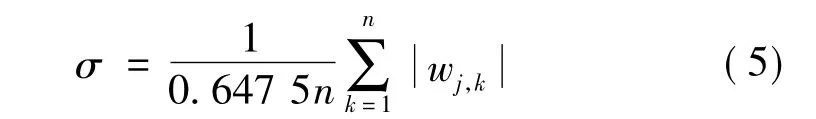
3.2 改进的阈值函数
由于软、硬阈值函数自身都存在一些缺陷,使重构信号存在一定的偏差,并且还会出现振荡,因此需要对阈值函数进行改进,改进的思想是要让小波系数的偏差尽量减小,要在小波空间中连续,还要具有高阶导数,为此,本文引入一种改进的阈值处理函数[7-8]
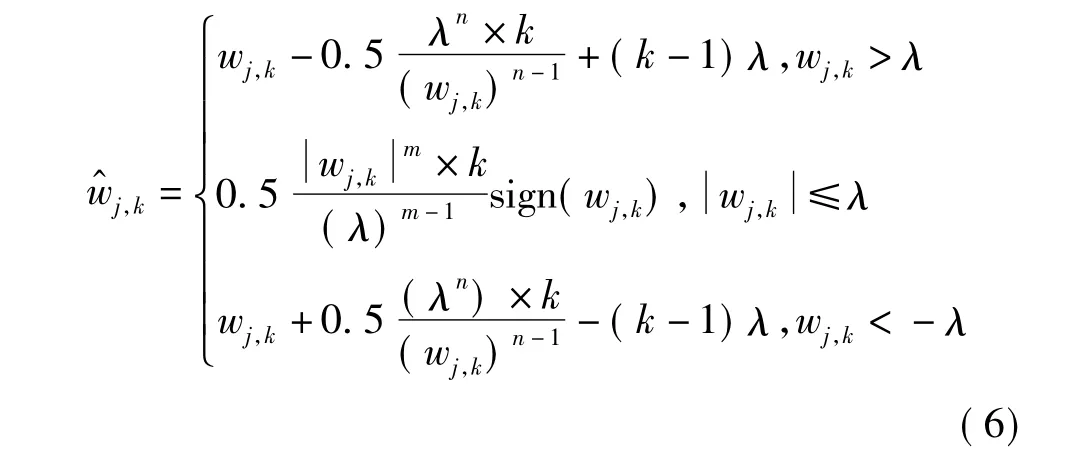
式(6)中,m、n、k是改进阈值函数的调整因子,它们增强了阈值函数的灵活性。参数m、n决定了阈值函数的形式,参数k的取值在0~1之间,若k取0,则该阈值函数相当于软阈值函数,若k取1,则该阈值函数相当于硬阈值函数。因此,可调节参数k能够克服硬阈值函数的不连续性和软阈值函数在处理小波系数时存在的恒定偏差,同时也保留了软、硬阈值原有的优点。改进的阈值函数具有无穷阶连续导数,为小波自适应阈值的选取提供了基础。改进的阈值函数图如图2所示。

图2 改进的阈值函数图
4 自适应阈值选取算法
传统的阈值函数会产生过扼杀现象,在实际应用中效果欠佳。由于噪声具有负奇异性,其幅度和稠密度随尺度增加而减小,但信号则相反。随着尺度级数的增加,由噪声所控制的模极大值的幅度和稠密度会快速减少,而信号的模极大值的幅度和稠密度会明显增大。可见,在同一级尺度上都采用同一阈值显然不合适,因为在较低尺度上,会去除有用信息,在最大尺度上会留下部分噪声[9-10]。
自适应阈值是一种采用最小风险量所对应的小波变换系数作为阈值的自适应阈值选取算法。由巴什瓦定理可知,小波分解后系数的平方具有能量的量纲,因此,将分解后的小波系数平方后排序,给定一个阈值,求出对应的风险值,即得到它的似然估计,进行非似然最小化,得到所选的阈值,这是一种软阈值估计器。其具体算法[11]为:
(1)将每一层的小波变换后的系数经过平方由小到大排列,得到一个向量w=[w1,w2,…,wn],其中w1≤w2≤…≤wn,n为小波系数的个数。
(2)计算风险向量R=[r1,r2,…,rn],则
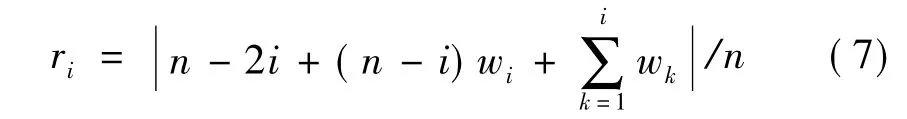
其中,ri为引入的风险向量元素,将上式多次迭代得出最小的ri,记为r0,并求出与之对应的wi记为w0。
(3)计算阈值 λ=σ(w0)1/2,其中 σ 的求解见式(4)。
按照上述算法将每一级尺度都看作相互独立,计算出一个与之最匹配的阈值进行降噪,最后再用各个尺度上降噪处理后的小波系数来重构信号。
5 仿真实验分析
为验证改进阈值方法的去噪效果,通过Matlab中的Wnoise函数构造一个长度为含噪信号,其噪声标准差为2,然后利用Sym8小波作为小波函数,分解层数为5层,采用改进阈值函数和自适应阈值去噪方法进行去噪,并与传统的软、硬阈值函数去噪方法进行比较,下面给出了信号在3种阈值函数下的去噪效果图。
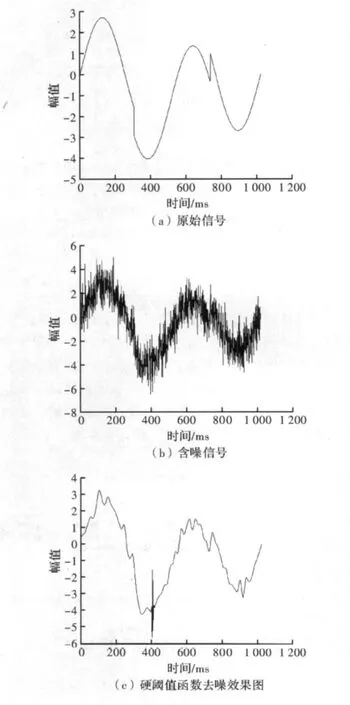
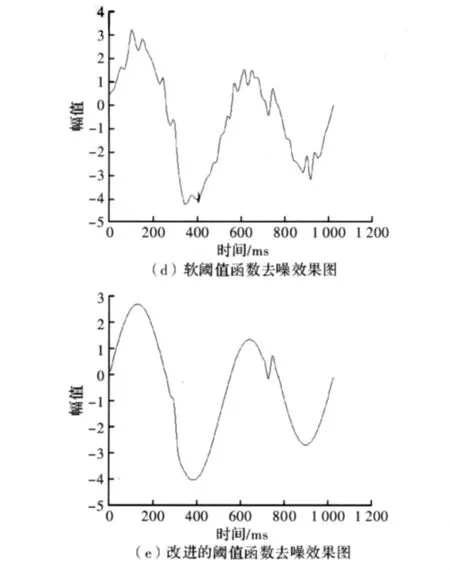
图3 不同阈值函数去噪效果图对比
表1给出了含噪信号经过3种不同阈值函数的信号去噪方法处理后的信噪比和标准差的数据对比。
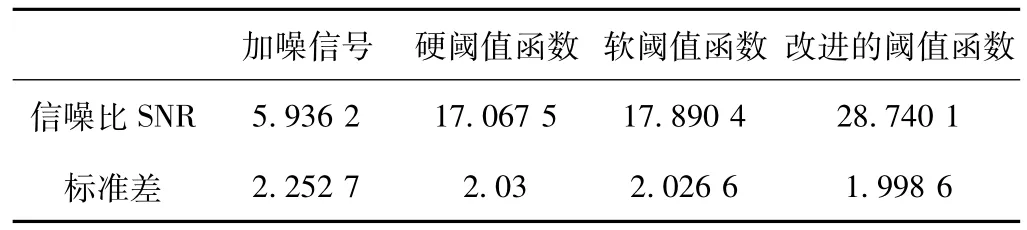
表1 不同阈值函数的去噪效果数据分析
通过从以上仿真图和数据分析对比表可以看出,采用改进阈值函数和自适应阈值的信号去噪效果要优于传统的软阈值去噪和硬阈值去噪效果,能有效地克服软阈值去噪方法中由于估计值与真实值之间的恒定偏差而带来的去噪误差,也能有效地抑制硬阈值去噪方法中易产生的信号振荡现象,较好地保留了信号的细节部分。
6 结束语
根据小波阈值去噪基本原理,提出了一种改进阈值函数和自适应阈值的信号去噪方法,改进的阈值函数兼顾了硬、软阈值函数的优点,同时又在一定程度上弥补了两种方法存在的不连续、振荡等缺陷。通过仿真实验可以看出,去噪效果无论在视觉上还是在去噪后信号的信噪比上都有了明显的改善,而且较好地保留信号的细节部分,提高了信号去噪的恢复能力。
[1]吴勇.基于小波的信号去噪方法研究[D].武汉:武汉理工大学,2007.
[2]翟振兴.基于小波变换的信号去噪研究[D].重庆:重庆大学,2010.
[3]吕瑞兰.小波阈值去噪的性能分析及基于能量元的小波阈值去噪方法研究[D].浙江:浙江大学,2003.
[4]曾守桢.小波去噪及其在信号处理中的应用[D].天津:天津大学,2007.
[5]李海东,李青.基于阈值法的小波去噪算法研究[J].计算机技术与发展,2009,19(7):56 -57.
[6]DONOHO D L.Denosing by soft– threshoulding[M].IEEE Trans on IT,1995,3(40):613 -627.
[7]王睿,山拜达拉拜.一种新阈值函数的小波信号去噪研究[J].通信技术,2011,44(1):50 -52.
[8]易方,李著信,苏毅,等.基于改进型小波阈值函数的输油管道磁记忆信号降噪方法[J].石油学报,2009(1):141-144.
[9]唐进元,陈维涛,陈思雨,等.一种新的小波阈值函数及其在振动信号去噪分析中的应用[J].振动与冲击,2009(7):118-121.
[10]李冠,吴尽昭,范明钰.基于小波的信号去噪分析[J].通信技术,2010,43(9):79 -81.
[11]袁兰敬.小波变换在信号去噪中的应用[D].北京:中国地质大学,2008.
