基于蜂群优化模糊聚类的遥感图像变化检测

贾彩杰

(西安电子科技大学理学院，陕西西安 710071)

遥感图像变化检测是通过对同一地区不同时期的两幅或多幅遥感图像的比较分析，以及图像之间的差异得到所需的地物变化信息，因此遥感图像变化检测为国土资源调查［1］、城市规划、森林资源检测、环境变化检测、灾害预报与评估［2］等方面发挥了重要作用。目前变化检测的研究方法可分为两种:第一是比较后分类法，即先构造一幅差异图像，然后对这幅差异图像进行处理;第二是分类后比较法，即先对每个时相的图像进行分类，然后对分类后的各时相图像进行比较，变化检测中常用的方法是第一种比较后分类法。在遥感图像中，按照是否有已知训练样本的分类数据，将分类法分为两大类:监督分类和非监督分类。由于监督分类需要对类别进行学习，而非监督分类则由图像数据本身的统计特征来决定，不需要先验条件。模糊C均值聚类算法是一种能自动对样本点进行非监督分类的方法，因此在遥感图像变化检测中广泛应用。

在遥感图像变化检测中，由于像素不一定是单纯的一种地物信息，有可能是混合地物类型的反映。那么，利用传统的“硬”分类方法进行图像分类无法获得较高精度，为改善这种情况，一种基于模糊集的模糊分类器被提出。1965年Zedeh创立了模糊集理论［3］，为用模糊的方法处理聚类问题奠定了基础。Dunn首先将最小方差聚类方法模糊化，提出了fuzzy ISODATA聚类方法［4］，其后 Bezdek将该方法推广为一般 FCM聚类算法［5］。目前对差异图(DI)进行聚类常用的一种模糊聚类算法就是模糊C均值聚类算法［6］。

由于FCM聚类算法本质是用梯度下降的方法寻找最优解，所以存在局部最优问题，并且收敛速度受初始值的影响较大。Karaboga［7］在分析蜂群行为规律的基础上，将蜂群模型用于研究函数的数值优化问题，系统地提出了ABC算法，由于ABC算法具有全局最优和收敛速度快等特点，因此结合两种算法的优点提出了基于蜂群算法优化模糊C均值(ABC－FCM)［8］，将此算法用于遥感图像的变化检测中。不同于文献［8］的是，文中用ABC算法代替FCM中优化聚类中心的部分，实验结果表明，该方法具有检测率高和速度快等优点。

1 基于ABC优化FCM遥感图像变化检测

针对FCM算法容易陷入局部最优及对初始解的敏感性，结合遗传算法(GA)［9］的全局最优，A.Ghosh等人将FCM算法和GA结合到遥感图像变化检测中［10］，实验证明GA－FCM算法在收敛速度和检测结果上都有明显提高。遗传算法(GA)中的人工蜂群算法是模仿蜜蜂行为提出的一种优化方法，人工蜂根据各自的分工进行不同的采蜜活动，并实现蜜源信息的共享和交流，从而找到最佳蜜源(最优解)。蜂群系统包括3个元素:蜂群、蜜源和蜜蜂个体间的信息交流。蜂群按分工不同可分为采蜜蜂、观察蜂和侦查蜂，ABC算法搜索流程可分为3个阶段:(1)采蜜蜂在邻近的蜜源进行一次邻域搜索并记忆蜜源的花蜜量。(2)采蜜蜂和观察蜂分享蜜源信息，观察蜂选择一个蜜源并在该蜜源的邻近内选择一个蜜源。(3)得不到改进蜜源处的采蜜蜂放弃该蜜源变成侦查蜂，搜索新的蜜源。

因此结合ABC算法和FCM算法的各自优点提出了ABC优化FCM的算法，该算法利用比值和差值融合的办法得到差异图，再用ABC算法中的采蜜蜂所在位置(初始蜜源)作为初始聚类中心，增加种群的多样性，利用对初始蜜源的邻域搜索对初始聚类中心进行更新，增强算法的全局搜索能力，用FCM算法中的目标函数作为ABC算法的目标函数，当满足停止条件时，输出检测结果。算法的具体步骤如下:

Step1对待检测的两时相遥感图像进行预处理，主要有图像配准、图像增强、几何校正等，目的是为了排除不必要的干扰得到较好的差异图像。

Step2利用多时相遥感图像X1和X2的灰度值的差值和比值融合的方法计算差异图(DI)的灰度值，具体方法如下

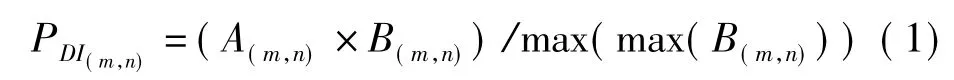
Step3用ABC－FCM方法对差异图进行聚类。

首先，设置初始化参数，种群规模N=20，采蜜蜂和观察蜂分别为10，最大循环次数Maxcycle=200，作为停止条件，限定蜜源不能改进的次数limit=30，聚类数cluster=2，模糊指数m=2。

其次，随机产生初始蜜源Foods，利用式(2)求该组蜜源的目标函数，并求出相应的适应度值

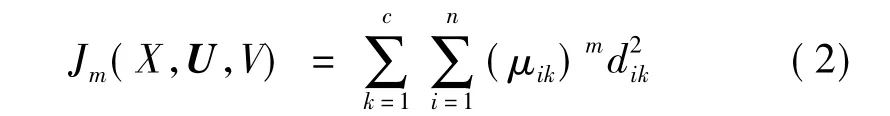
其中，X={x1，x2，…，xn}是n个模式样本集，xi是X的第i个模式，是维数为P的向量，把这n个模式划分成c类V={v1，v2，…，vn}，vi(1≤k≤c)是第k类的聚类中心，维数也为p。模糊划分矩阵U=［μik］c×n∈Mfcn，划分空间为

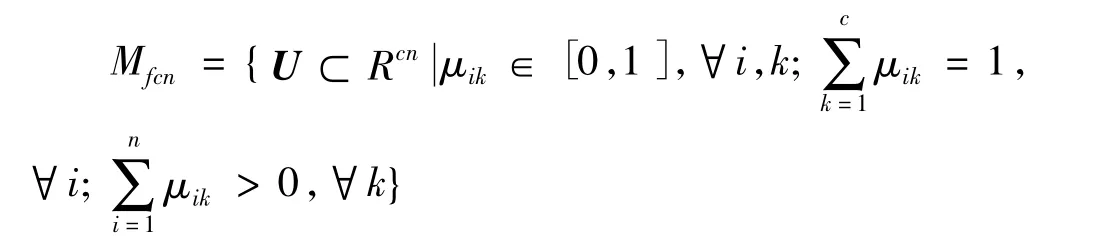
式中，μik表示第i个元素属于第k类，计算式为

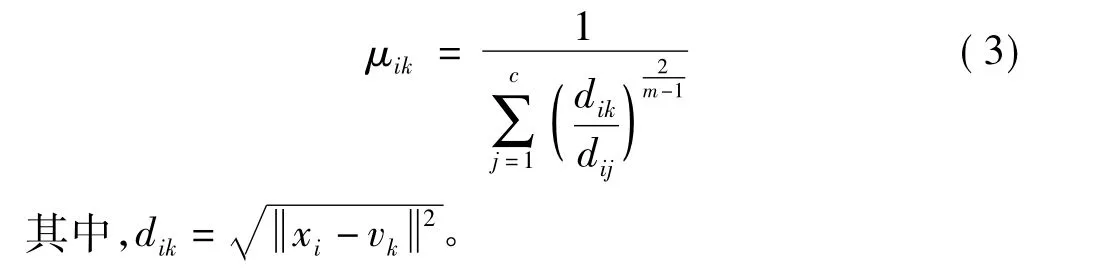
这部分利用的是先随机生成初始蜜源，即初始聚类中心，然后计算每个模式到每个聚类中心的欧氏距离，最后由距离得到模糊矩阵，从而算出目标函数。由于初始蜜源由N/2个种群组成，增加了初始聚类中心的多样性，不容易使算法陷入局部最优，更容易搜索到全局最优的聚类中心，也使算法有较强的鲁棒性。而之前的FCM算法，是先随机生成模糊矩阵，由式(4)得到初始聚类中心，再计算欧氏距离，由距离更新模糊矩阵，直到满足停止条件Ut－Ut－1≤ε，t为循环次数，ε为预先给定的小正数，即得到最终聚类结果，这样利用梯度下降寻找最优的过程很容易陷入局部最优，对初始解的依赖性大

最后，记忆适应度值最大的蜜源Xi，i=1，…，10，通过式(5)随机产生一个候选解Vi，计算该解的目标函数值和适应度，比较Vi和Xi适应度值的大小，保留适应度值较大的解

其中，k、j均为随机选择的下标，k∈{1，2，…，10}，且k≠i，j={1，2};Φij为［－1，1］之间的随机数。

Step4用式(6)计算每组蜜源适应度的概率，观察蜂阶段以概率进行轮盘赌选择蜜源Xi，并用式(5)产生候选解Vi，保留适应度值较大的解

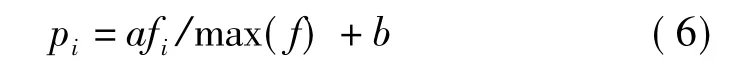
其中，fi为第i个蜜源的适应度值，i∈{1，2，…，N};a=0.9和b=0.1为事先给定的数。

Step5超过限定次数limit的解即被认为不能改进的蜜源，则该处的采蜜蜂变成侦查蜂利用式(7)搜索新的蜜源

Step6直到满足停止条件，即iter＜Maxcycle，迭代停止，输出全局最优蜜源，即为最优聚类中心。

Step7结合FCM算法，利用差异图的灰度值和最优聚类中心，算出模糊矩阵，根据模糊矩阵即可将差异图的灰度值划分为变化类和未变化类，输出最终的二值图像。

Step8为得到更好的结果，对二值图像进行后期处理，文中用的是中值滤波，窗口大小为［3，3］，滤波后可以除掉较小噪声的影响，起到平滑作用，得到较好最终结果。

2 实验结果及分析

2.1 实验数据描述

为验证算法的有效性，并与经典的FCM算法得到的检测结果进行比较分析。考虑遥感图像的两组数据集，第一组数据集的原始图像是 ATM(Airborne Thematic Mapper)3波段位于英国Feltwell村庄的一个农田区的图像，如图1(a)所示，图1(b)是其模拟变化图像，通过模拟地球的天气变化和电磁波辐射特性等因素影响并人工嵌入一些变化区域得到的。两幅图像大小均为470×335像素，灰度级为256，其参考变化如图1(c)所示。

图1 模拟遥感数据集图像和参考变化图

第二组数据集由墨西哥郊外的两Landsat7ETM+(Enhanced Thematic Mapper Plus)第4波段光谱图像组成，图2(a)显示的是2000年4月18日地球卫星情况，图2(b)为2002年5月20日该地区被大火破坏后的卫星图，两幅图像大小均为512×512像素，灰度级为256，其参考变化图如图2(c)所示。

2.2 变化检测结果及分析

图2 真实遥感数据集原始图像及变化参考图

(1)Feltwell村庄的农田区的变化检测结果及分析。变化检测结果如图3所示，图3(a)是差异图像，分别用FCM算法和本文算法对此差异图进行聚类，检测结果分别为图3(b)和图3(c)，由图可以看出，文中算法图像孤立像素点明显减少，最关键的是文中算法在处理边缘地区有明显优势。文中算法与FCM算法检测结果比较如表1所示，文中算法在总错误数和漏检数都比FCM算法要低，正检率也比FCM算法高，说明在分类结果上本文算法较FCM算法准确。另外图5(a)和图5(b)分别为FCM算法和本文算法的目标函数收敛曲线图，文中算法独立实验5次，收敛结果基本一致。由图可知，FCM算法在迭代过程中没有出现反复情形，说明FCM算法在聚类时有可能陷入局部极小，并且文中的目标函数值明显比FCM的目标函数值小，说明文中算法找到的聚类中心更加准确。

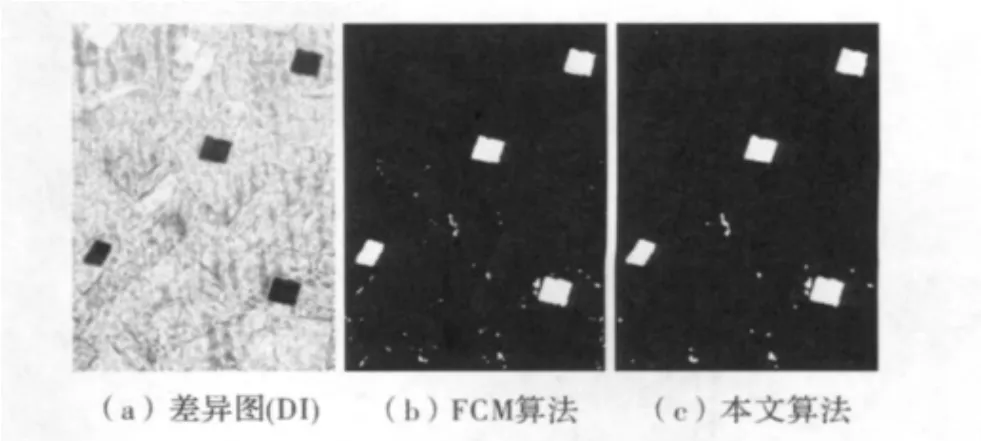
图3 两种算法对模拟遥感数据集的变化检测结果

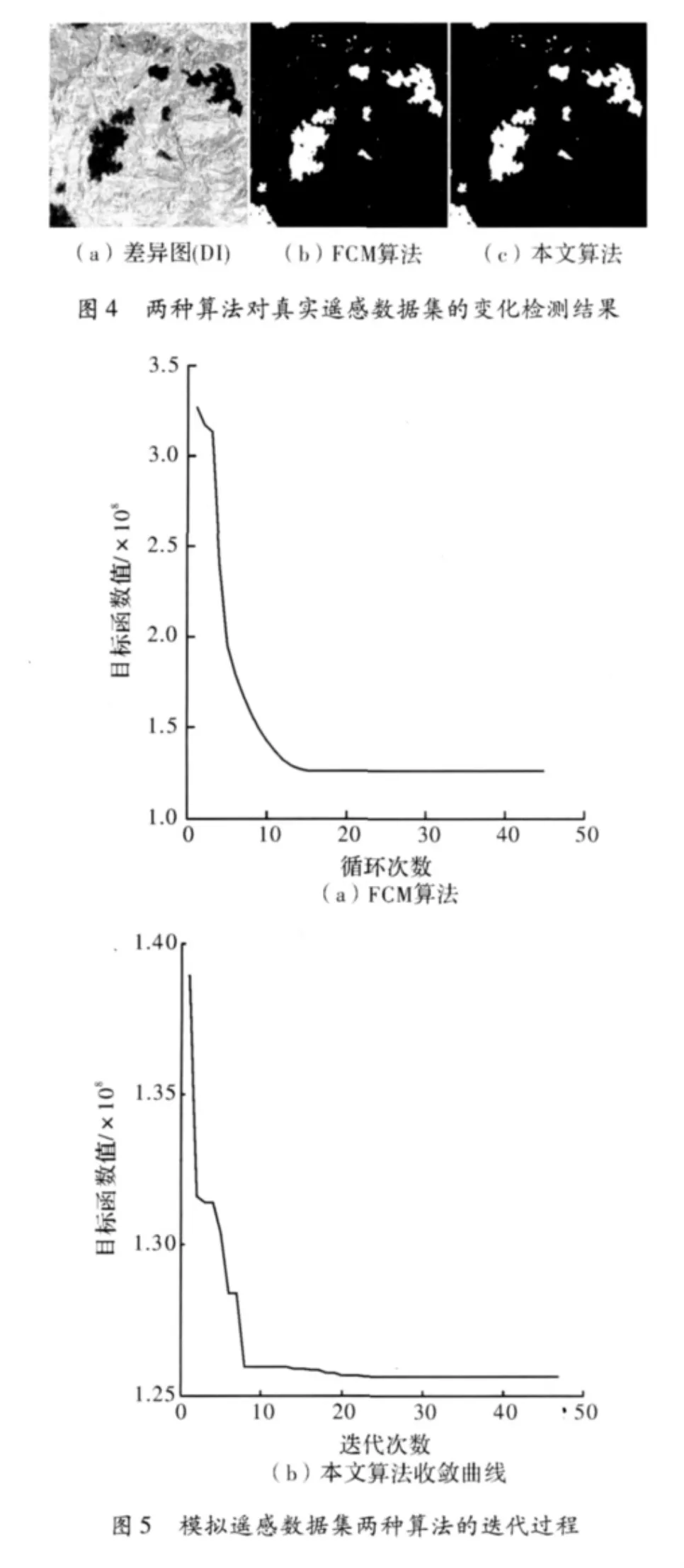
(2)墨西哥郊外地区火灾变化检测结果及分析。变化检测结果如图4所示，图4(a)为差异图，分别用FCM算法和文中算法对差异图进行聚类，检测结果分别为图4(b)和图4(c)，显然图4(c)的孤立像素点相对图4(b)少，在边缘处比较光滑，检测结果比较如表2所示，文中算法的总错误数和漏检数都比FCM算法的低，正检率有所提高。图6(a)和图6(b)分别为FCM算法和本文算法的目标函数收敛曲线图，由图可知，文中算法的收敛速度快，并且目标函数值比FCM算法的目标函数值小。

表1 Feltwell村庄的农田区的变化检测结果及分析

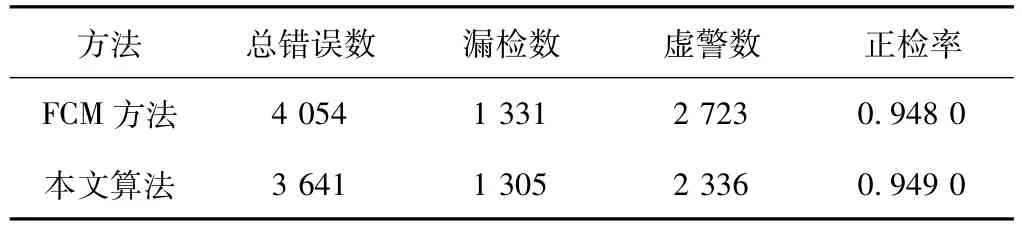
表2 墨西哥火灾变化检测结果与分析

3 结束语

针对FCM易陷入局部最优和ABC优化算法具有全局最优性，提出了一种新算法，并将新算法应用于遥感图像的变化检测中，实验证明该混合算法具有较好的检测能力、检测速度快及易实现全局最优。根据人工蜂群算法的全局最优，可将其应用到图像处理中的图像分割、人脸识别等领域。

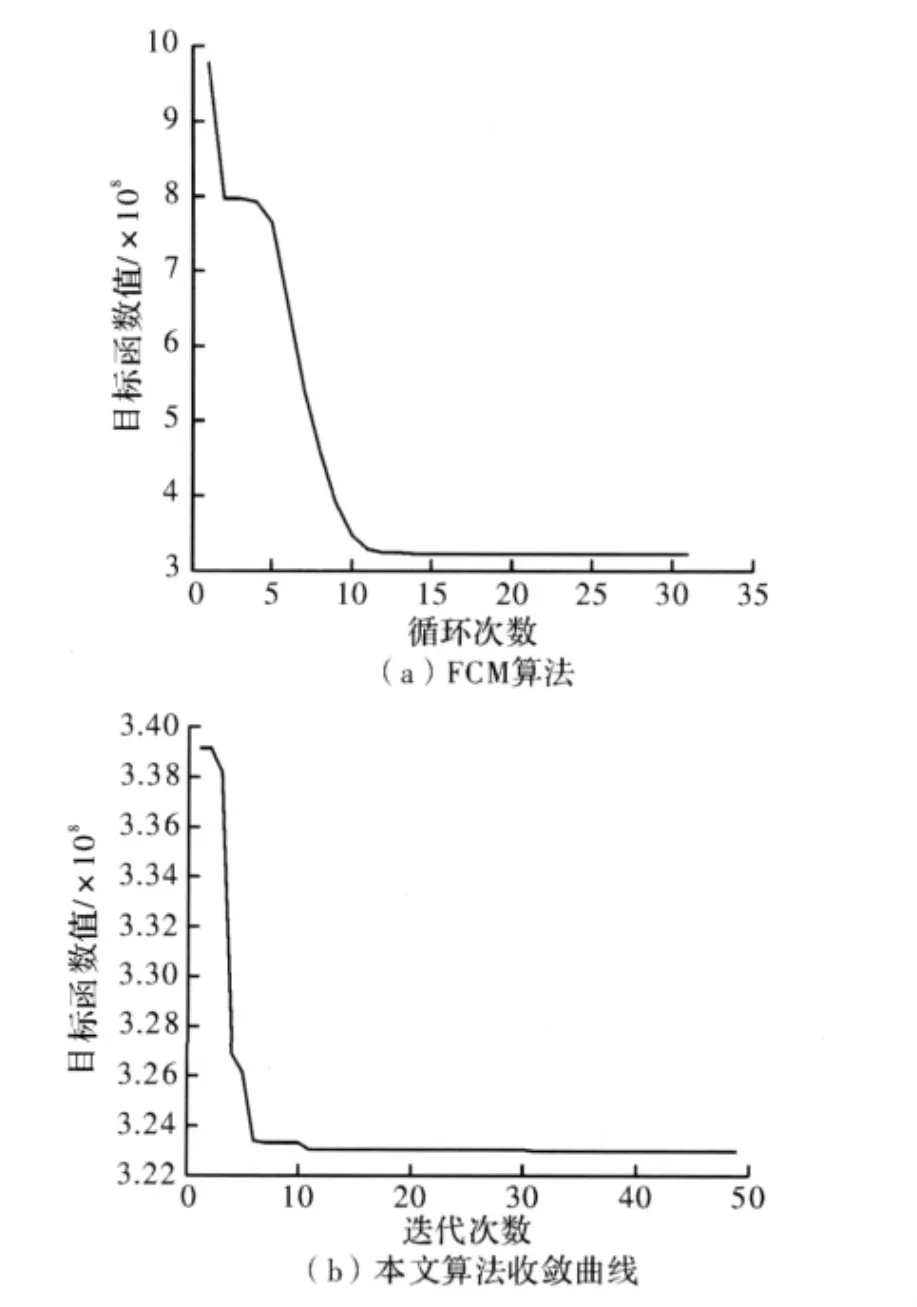
图6 真实遥感数据集两种算法的迭代过程

［1］CIHLAR J，PULTZ J T，GRAY A L.Change detection with synthetic aperture radar［J］.International Journal or Remote Sensing.1992，13(3):401 －414.

［2］HAME T，HEILER I，SAN J.An unsupervised change detection and recognitionsystem for forestry［J］.International Journal of Remote Sensing，1998，19(6):1079 －1099.

［3］ZADEH L A.Fuzzy sets［J］.Information and Control，1965(8):338－353.

［4］DUNN J C.A fuzzy relative relative of the ISO DATA process and its use in detecting compact well separated clusters［J］.Journal of Cybernetics，1974，3(3):32 －57.

［5］BEZDEK J C.Pattern recognition with fuzzy objective function algorithms［M］.New York:Plenum Press，1981.

［6］GHOSH S，MISHRA N S，GHOSH A.Unsupervised change detection of remotely sensed images using fuzzy clustering［C］.International Conference on Advances in Pattern Recognition，2009，9:385 －388.

［7］KARABOGA D.An idea based on honey bee swarm for numerical optimization［R］.Ultra:Erciyes University，Engineering Faculty，Computer Engineering Department，2005.

［8］赵小强，张守明.基于人工蜂群的模糊聚类算法［J］.兰州理工大学学报，2010，36(5):79 －82.

［9］GOLDBERBG D E.Genetic algorithms in search［C］.Optimization and Machine Learning.Addison － Wesley，Reading，1989.

［10］GHOSH A，MISHRA N S，GHOSH S.Fuzzy clustering algorithms for unsupervised change detection in remote sensing images［J］.Information Sciences，2011，181(3):699 －715.