丁坝间潮滩地貌变化的经验正交函数分析

郭凤霞，邱建立，吴松华，郭国明

（1.浙江大学 海洋科学与工程学系，浙江 杭州 310058；2.中交上航局航道建设有限公司，浙江 宁波 315200；3.北京科技大学 物理系，北京 100083）

0 引言

WINANT和INMAN［1］曾用经验正交函数法对沙质海岸的季节性变化作过定量分析，其基本思想是将海滩剖面变化中起主导作用的因素，分解为3个表示海滩剖面基本变化的因子，进而分析海滩地形变化的时空特征。陈子燊 等［2－4］也用类似的方法分析了粤西水东湾海滩剖面变化的空间过程及时间震荡特性。金庆祥 等［5］利用经验正交函数分析了杭州湾北岸金汇港泥质潮滩的变化。然而，对于淤泥质潮滩变化的定量研究较少，或是仅仅选择了一两条剖面进行研究。

本文以浙江瑞安丁山建成丁坝后的淤积质潮滩为例，用经验正交函数法（下文简称EOF）对1979—1982年3a间的逐月高程资料进行分析，对建成丁坝后淤泥质潮滩的冲淤情况进行定量研究。将3条丁坝间10条剖面和大致位于同一水深的3条等深线历时3a的逐月测量资料分别进行EOF分析，得到反映整个潮滩90%以上变化的3个经验正交函数，即表示潮滩总体冲淤变化的第一特征函数，表示季节性冲淤变化的第二特征函数和表示偶然因素扰动引起冲淤变化的第三特征函数。用这3个经验正交函数的线性组合来反映整个潮滩的空间和时间变化特征。空间特征函数代表潮滩地形变化，时间特征函数代表地形变化的时域特征，海滩剖面的时空变化过程在一定程度上反映了过程－响应系统的主要海滩过程。本文借助统计分析和动力机理分析相结合的方法，分析潮滩冲淤变化与动力要素的关系。利用“场”的概念从整体上分析潮滩的变化，克服了以往用单个点来描述潮滩剖面变化的局限性，从整体上揭示浙江瑞安丁山潮滩剖面建立丁坝后的时间和空间变化特征，从中不仅可以得到详细的淤泥质潮滩建立丁坝后潮滩变化的一般规律，而且有助于对潮滩地貌进行“过程－响应”分析和地貌演变的预测。

1 研究区概况及统计分析方法

1.1 研究区地理位置和气象条件

本文研究区域为浙江瑞安丁山淤泥质潮滩，位于飞云江口北侧27°46′N、120°45′E（图1），所建丁坝为丁山滩涂促淤工程，包括4条长丁坝和1条顺岸坝，本文选取3条丁坝（3＃丁坝，4＃丁坝和北丁坝）间2个潮滩（北丁坝和4＃丁坝间的梅头北平面，4＃丁坝和3＃丁坝间的梅头南平面）内10条剖面（A～J）及大致位于同一水深的3条等深线（a～c）上1979—1982年间3a内各个测点逐月测量的高程数据（以吴淞零点为基准面）进行分析研究。丁坝的具体地理位置和各测点位置见图2及表1［6］。

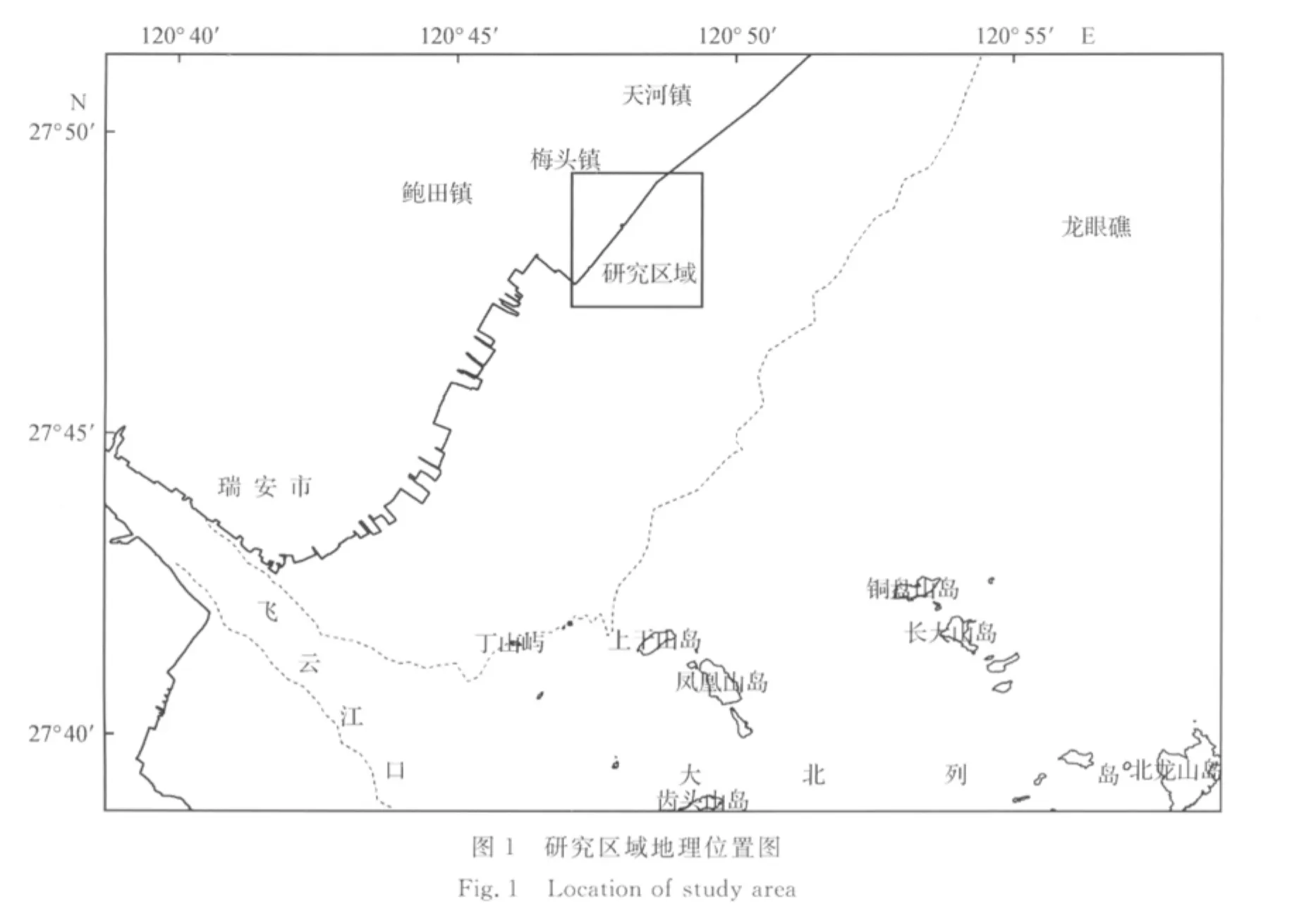
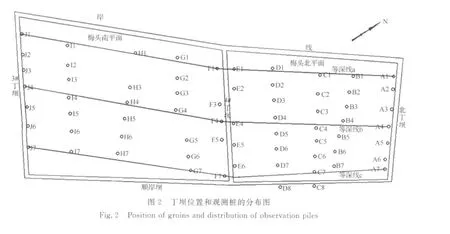
表1 丁坝情况简介［6］Tab.1 Position，length and alignment of groins［6］

统计资料显示，瑞安（飞云江口）多年平均潮差为4.24m。潮差以9月最大，1月最小，其量值差约为0.22m。该研究海域处于季风区，冬季盛行偏北风；夏季盛行偏南风；春、秋季为季风交替时期，偏南和偏北风交替出现。波向的分布频率基本与风向频率一致，冬季波浪以偏北向浪为主；夏季以东到东南向为常浪向；春季也以东到东南向浪为主；秋季为西南气流转偏北气流，处于交替过程中，9月波向分布类似于夏季，10月和11月类似于冬季［7］。

1.2 经验正交函数的统计分析方法

本文选用的数据为北丁坝和4＃丁坝之间的梅头北平面以及4＃丁坝和3＃丁坝之间的梅头南平面中10条潮滩剖面（A～J）和3条大致位于同一水深的等深线（a～c）的高程资料（图2）。各观测桩每月测量1次，为期3a重复测量，测量点数为n，测量次数为x，这些数据可组成原始高程矩阵Anx。数据处理方法为：

首先，计算高程距平值：

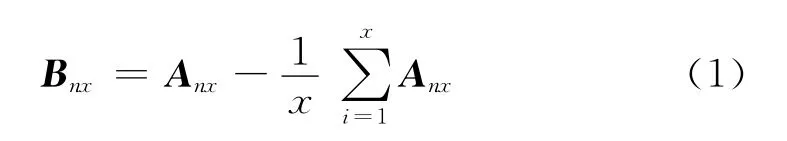
由原始高程矩阵得到高程距平矩阵B：

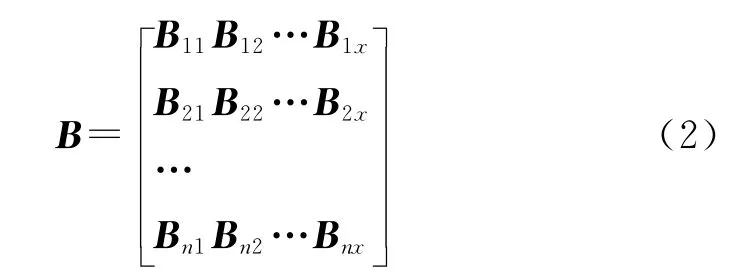
然后，对距平矩阵B进行经验正交函数展开：

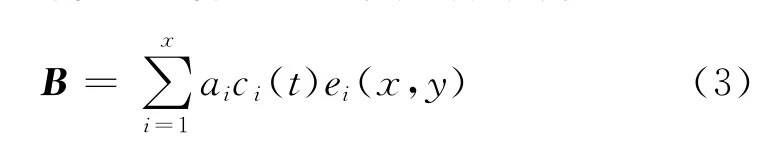
式中：ai为各个特征函数权重系数，ai＝（λinxnt）1／2，nx为各剖面水深测点数，nt为水深测量次数；ci（t）为时间特征函数；ei（x，y）为空间特征函数，具体计算方法见文献［1］和［4］。由雅克比旋转方法得到B空间协方差矩阵的特征值λ和空间特征向量ei；通过正交变换，计算出各空间特征向量对应的时间特征向量et。

由最大的3个特征值λ1，λ2和λ3提取占海滩剖面数据总方差90%以上的空间特征函数ei（x，y）：

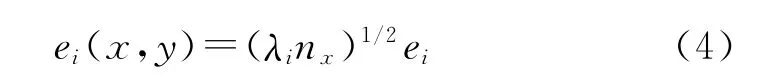
和对应的时间特征函数ci（t）：

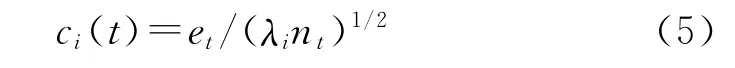
其余的特征函数则视为随机过程而不计。整个矩阵便可由前3个特征函数的线性组合来表示，即表示潮滩总体冲淤变化的第一特征函数，表示季节性冲淤变化的第二特征函数和表示偶然因素扰动引起冲淤变化的第三特征函数，这些特征函数的线性组合已反映出原始矩阵的基本情况，能客观地反映出淤泥质潮滩在丁坝影响下的基本变化规律。

由于某些观测桩被破坏，进行A～J剖面EOF计算时测量总数n的取值范围为5～8，而对3条等深线a、b、c进行EOF分析时n分别取9、9和8。本次测量历时5a多，积累了丰富的高程资料，本文选取其中完整的3a高程序列数据，平均1个月测量1次，测量次数x＝36。

2 结果与讨论

2.1 丁坝作用下潮滩地形空间分布变化

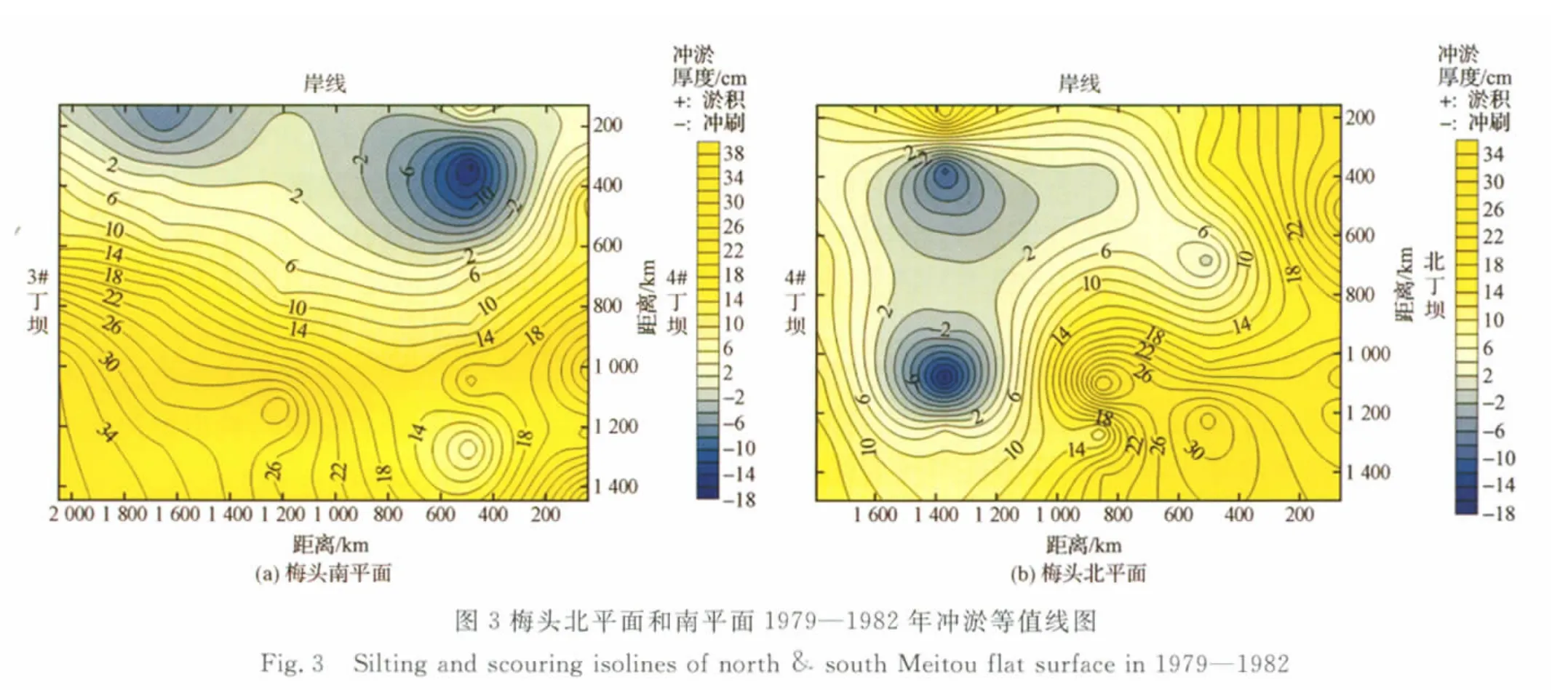
2.1.1 潮滩地形平面变化特征

图3为根据1979年12月—1982年12月丁坝间潮滩剖面的高程数据，得到的3条丁坝之间2个平面的冲淤等值线。由图3可知，丁坝建成后的潮滩淤积效果明显，梅头南平面3a平均淤积量为31.7cm，梅头北平面则为30.5cm。但淤积量在平面上分布并不均匀，一般情况为离岸越近，淤积量越小，即丁坝间平面内各测量桩所处滩面越高，淤积愈慢。梅头北平面靠近岸线部分淤积，中部略有冲刷，靠近海一侧淤积明显。而梅头南平面内丁坝内侧，靠近岸线部分冲刷严重，最大冲刷量达16cm，离海较远端则淤积非常明显，最大淤积量达到34cm。总体而言，淤积面积远远大于冲刷面积，靠近3＃丁坝南侧和北丁坝南侧形成明显堆积体，潮滩内形成弧状等深线。这与MARC和DEAN［8］研究的关于建立丁坝后岸滩平面形状的变化相一致。

2.1.2 潮滩地形剖面变化特征

因各剖面变化规律基本一致，限于篇幅，仅选择A和J两条剖面加以说明（图4）。

由图4可见，1979—1982年A和J两条剖面均呈淤积状态，经计算，其余8条剖面也都有不同程度的淤积，只有D和F两条剖面上中部和近岸几个点表现为冲刷，潮滩整体呈淤积状态。A剖面靠近北丁坝位置，丁坝根部和向海侧淤积幅度明显较大，结合图3b可知，丁坝根部有堆积棱体，向海一侧有沙嘴形成。由于丁坝作用，在其根部，岸线急剧向海转折，沿岸输沙阻断，泥沙落淤，造成丁坝里侧（潮滩内）泥沙淤积，形成堆积棱体；被阻断的沿岸输沙沿丁坝输移，在丁坝头部，由于顺岸坝的共同作用，造成沿岸泥沙大部分在此落淤，形成沙嘴。同理，J剖面靠近3＃丁坝位置，在向海侧（J7点）潮滩淤积量明显高于向岸侧（J1点），但剖面形状基本变化不大。

2.2 丁坝作用下地形变化的空间特征函数分析

用经验正交函数的统计方法对每条剖面和等深线上的观测桩高程进行计算，所得特征值和累计频率列于表2。

由表2可见，前3个特征函数的累积频率基本达到85%，基本可以反映出剖面变化的一般规律。10条剖面的前3个空间特征函数线的变化规律大致相同，故只选择A、E、H和I四条剖面进行详细分析。各典型剖面及等深线的前3个空间特征函数见图5～图7。

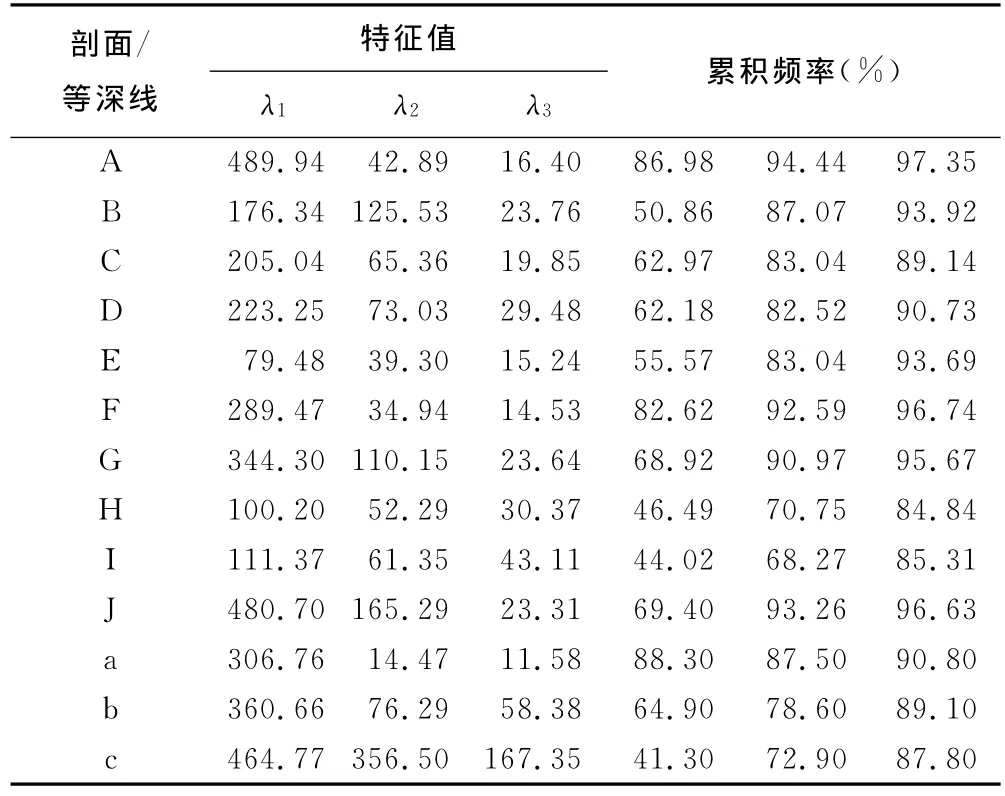
表2 各剖面特征值和累计频率Tab.2 Characteristic value and total accumulative frequency for each profile

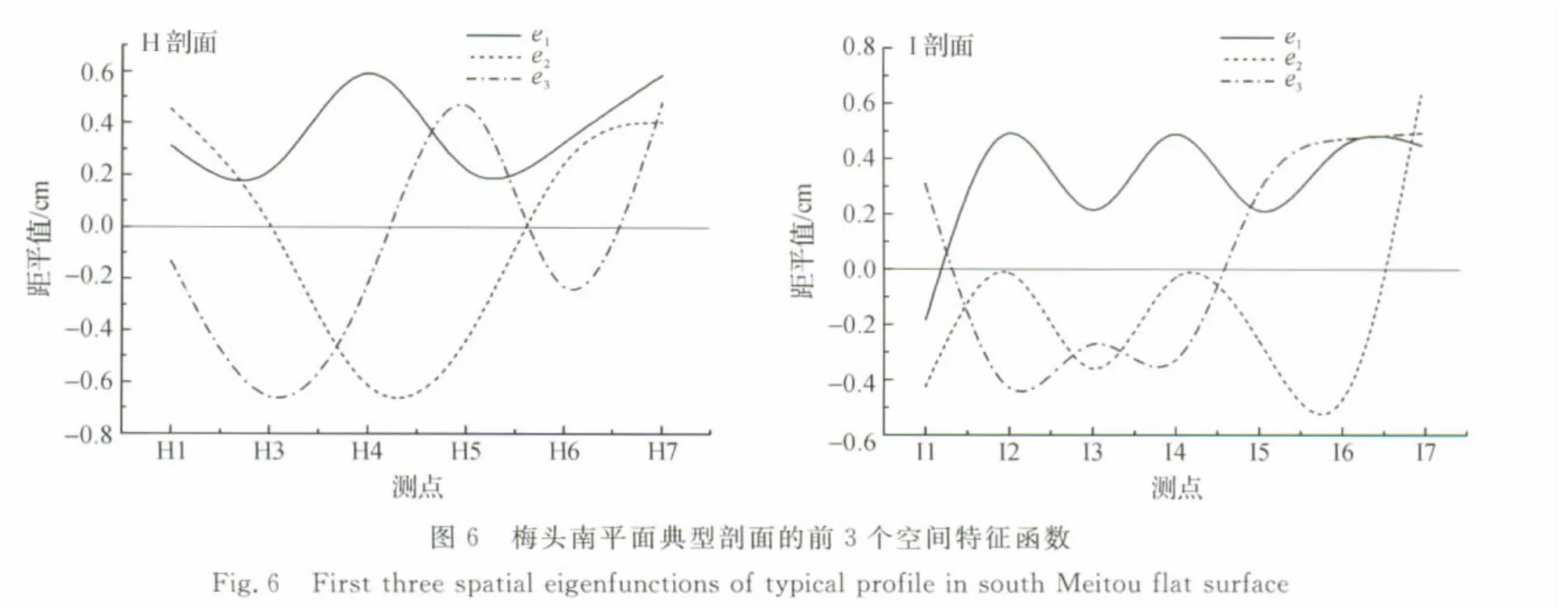
由图5和图6可知，潮滩内各个点的第一空间特征函数距平值（e1）变化趋势不大，且基本为正值，表明潮滩内地形变化的首要特征是淤积。E、H和I剖面离岸较远的测点距平值较大，表明丁坝向海一侧淤积明显，丁坝根部淤积效果不明显。而I1点距平值为负值，表明梅头南平面丁坝根部为冲刷。由图7和表2可知，离岸较近的a等深线，第一特征函数贡献率为88.30%，B1～E1和G1点为淤积，其余各点为冲刷，这对应了前述冲淤变化中梅头北平面离岸较近处整体淤积，而梅头南平面略有冲刷。等深线b的第一特征函数贡献率为64.90%，且第一特征函数几乎全为正值，表明此处潮滩整体淤积。而等深线c处C7、I7和J7之间特征函数为负值，表明此处冲刷，但冲刷量较小。其余各点第一特征函数值则较大，可见等深线c处大部分测桩点淤积明显，与前文2.1.1节平面冲淤变化计算结果中“梅头南平面向海侧淤积量较大”一致。由表2可知，10条剖面的第一特征函数占到总体的50%～80%，与 MARC et al［8］通过模型研究的关于丁坝建立之后潮滩变化结果相一致，研究区域在建成丁坝后的最显著特征是淤积，第一特征函数反映了潮滩的总体冲淤变化特征。第二特征函数对潮滩变化的贡献率为10%～20%。图5和图6中第二特征函数距平值（e2）有正有负，表明潮滩内既有淤积，又有冲刷。通过对应于第二特征函数的时间特征函数分析可知，10条剖面的第二时间特征函数均表现出周期性变化。由第二特征函数计算结果得到，夏季梅头北平面平均冲刷0.03cm，梅头南平面冲刷1.2cm；冬季梅头北平面淤积0.24cm，梅头南平面淤积1.7cm，因此，第二特征函数代表了潮滩剖面的季节性变化，反映了海滩泥沙向、离岸运动的季节性旋回，其表现为冬淤夏冲，冬季为淤积期，夏季为冲刷期。第三特征函数所占比率为5%～10%，系偶然因素扰动引起的冲淤变化。由图5和图6可知，第三特征函数（e3）波动较大，说明此地滩面变化受台风、风暴潮等偶然因素影响较大。

2.3 潮滩剖面时空变化与各种动力因素之间关系的时间特征函数分析

潮滩剖面的形态是各种动力因素相互作用于海岸的结果。潮滩剖面始终和波浪特征紧密联系，潮滩以其物质组成和剖面形态来响应动力过程［3］。本文从潮滩剖面特征的时间分布特征来探求海滩剖面的空间地貌动力成因。影响潮滩过程的动力因素包括潮流、波浪、沙的源与汇、地形、剖面形态和纳潮量等。时间特征函数为这些动力地貌过程的分析提供了一种有效的方法，不同的特征函数分别代表了潮滩上不同的地貌动力过程，分别反映了潮滩内不同的过程－响应系统。图8～图10为各典型剖面和等深线上与前3个空间特征函数对应的时间特征函数。

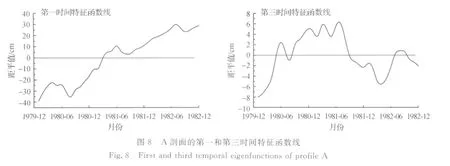
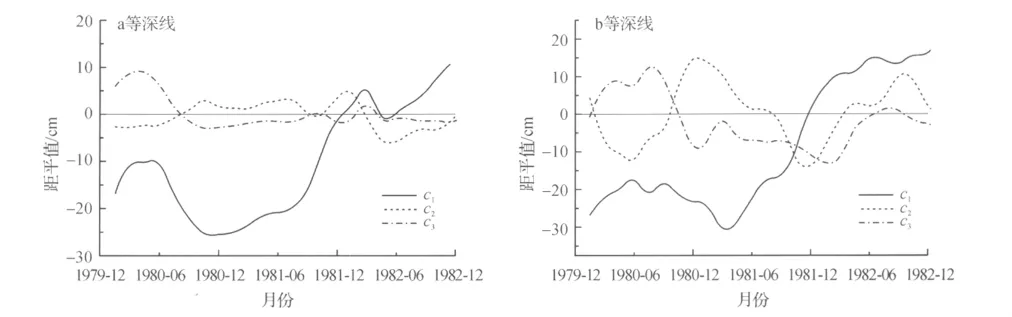
图10 等深线a和b的前3个时间特征函数Fig.10 First three temporal eigenfunctions of isobath profile a and b

第一时间特征函数为平均潮滩函数，反映的是岸滩总体冲淤变化，即潮滩在建成丁坝后的整体变化趋势。由于各剖面上第一时间特征函数曲线趋势基本一致，因此只给出A剖面的时间特征函数曲线（图8）和a、b等深线处的时间特征函数曲线（图10）。由前3个空间特征函数可计算出年淤积量为梅头北平面12.8cm，梅头南平面7.7cm，多年观测桩观测资料计算的年淤积平均量为15cm，第一时间特征函数基本反映出潮滩变化的总趋势。A剖面第一时间特征函数和a、b等深线处的第一时间特征函数值随时间持续而逐渐增大，表示此特征函数的时间过程是逐步淤积的，尽管各个时间段内淤积量并不相等。图8～图10中各个剖面不同的时间特征函数线振幅（距平值）相差较大，表明各个不同动力过程对潮滩作用效果存在差异。由表2可知，λ1取值在50%～80%之间，即地形变化导致该研究区域水动力条件发生改变，由于顺岸坝的作用，落潮流流速下降，泥沙落淤，从而导致潮滩淤积，此过程对整个潮滩变化过程的影响比重为50%～80%。本海区属强潮流区，对于以淤泥质海岸为主的丁山潮滩，潮流是搬运泥沙的主要动力，塑造地貌的主要因素。由于同时存在的径流作用，该海区落潮流速大于涨潮流速，落潮流历时大于涨潮流历时［8］，因此，在丁坝和顺岸坝联合作用下，建立丁坝后必然会导致该区域落潮流流速下降，落潮历时更长，径流和涨潮流带进去的泥沙大部分能在潮滩内沉积下来，潮滩淤积。

潮滩各剖面的第二时间特征函数（图9，选择A、B剖面作代表进行分析）则表现出周期性变化，各剖面每年的第二时间特征函数值都为夏季小于冬季，具有明显的冬淤夏冲的特征。各条等深线上第二时间特征函数有正有负，表示等深线处潮滩在对应的时间节点上有冲刷或淤积，但季节性变化不明显（图10）。研究区偏南和偏北气流交替出现，决定了波浪季节性变化特点，此过程可以看成是潮滩对波浪这一动力过程的响应。由于夏季盛行东南季风，波浪以东到东南为常浪向，研究区域岸线走向为NE—SW向（表1），在东南常浪向影响下，沿岸流分量由南向北，丁坝位置为125°～135°走向，潮滩处于丁坝下游位置，此季节潮滩冲刷。而冬季则以偏北向浪为主，来沙较为丰富，潮滩淤积。另外，借助沿岸输沙率［9－10］、岸线平面形态数值模拟［11－13］也可以定性判断岸线变化为夏季侵蚀，冬季淤积。可以认为，第二时间特征函数所代表的周期性动力过程受季节性波浪影响显著。

研究区潮差9月最大，1月最小。1979—1982年各个潮滩1月和9月冲淤量计算值见表3。由表3可见，潮差大小与冲淤量大小的相关性不大，并且也没有规律显示潮差与冲淤存在定性关系。因此，季节性波浪引起的不同方向的沿岸流是引起冲淤季节性变化的主要因素，潮差则对这一过程影响不大。由表2中λ2频率计算值可见，波浪作用的动力过程对潮滩变化影响大致为10%～20%。

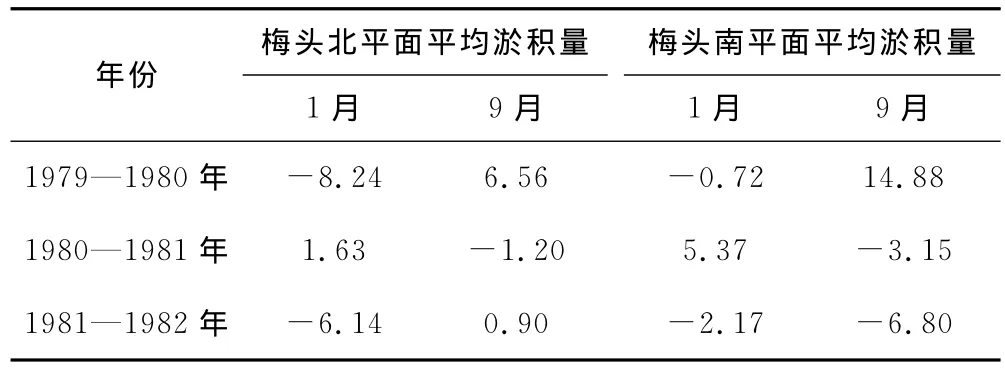
表3 潮滩内1月和9月的平均淤积量Tab.3 Average sedimentation of the tidal flat in Jan.and Sep.

第三时间特征函数反映的是风暴潮等偶然动力因素引起的滩面变化。由该地的水文资料可知，每年7—9月份，为各种偶然天气多发期，每次风暴潮等偶然天气过境都会引起波浪等动力条件的变化，这些变化引起泥沙输移量改变从而导致岸线变化。由于这些偶然因素的不规律性，代表这种动力过程的第三时间特征函数也具有不规律性（图10）。各种极端气候、风暴潮等偶然动力过程所占比重约为5%～10%。

综上所述，前3个时间特征函数曲线代表了与前3个空间特征函数对应的动力过程。其他动力过程由于对潮滩变化影响较小，可视为纯随机过程而不再考虑。

3 小结

本文应用经验正交函数法对浙江瑞安丁山建成丁坝后的潮滩连续3a高程数据进行分析认为：该方法不但较客观地反映了建立丁坝后潮滩地貌变化的一般规律，而且能反映出地貌变化的时空特性。前3个经验正交函数的线性组合，即表示岸滩总体冲淤变化的第一特征函数，表示季节性冲淤变化的第二特征函数和表示偶然因素扰动引起冲淤变化的第三特征函数，基本可以反映出该潮滩变化的总体趋势。用对应于前3个空间特征函数的时间特征函数分析可知，该潮滩地貌受潮流塑造作用明显，且受波浪季节性影响严重，潮滩变化具有明显的冬淤夏冲的特点。实践证明，这种统计方法对潮滩剖面变化进行定量分析不仅是可行的，而且有助于对潮滩地貌进行过程－响应分析和地貌演变预测。

（References）：

［1］WINANT C D，INMAN D L，NORDSTROM C E.Description of seasonal beach changes using empirical eigenfunctions［J］.Journal of Geophysical Research，1975，80（15）：1 980－1 986.

［2］CHEN Zi－shen.Analysis on spatial and temporal processes of beach profile variations［J］.Marine Science Bulletin，2000，19（2）：42－48.

陈子燊.海滩剖面时空变化过程分析［J］.海洋通报，2000，19（2）：42－48.

［3］CHEN Zi－shen，LI Chun－chu.Analysis on geomorphological dynamics of beach profile of intermediate transitional zone in arcshaped shore［J］.Marine Science，1990（2）：6－12.

陈子燊，李春初.弧形海岸中间过渡带海滩剖面地貌动态分析［J］.海洋科学，1990（2）：6－12.

［4］CHEN Zi－shen.Progress in studies on the shapes and dynamics of beach profiles［J］.Marine Science Bulletin，1997，16（1）：86－91.

陈子燊.海滩剖面形态与地形动态研究进展［J］.海洋通报，1997，16（1）：86－91.

［5］JIN Qing－xiang，LAO Zhi－sheng，GONG Min.The EOF method on analysis muddy temporal variations located in north Hangzhou Bay，Jinhui［J］.Acta Oceanologica Sinica，1988，10（3）：327－333.

金庆祥，劳治声，龚敏.应用经验正交函数分析杭州湾北岸金汇港泥质潮滩随时间的变化［J］.海洋学报，1988，10（3）：327－333.

［6］XU Xing－huang，SUN Ting－zhao，HUANG Jin－peng.Investigation on the effect of accelerating silt accumulation of the composite of groin system and detached dike［J］.Coastal Engineering，1985，3（1）：15－23.

许星煌，孙庭兆，黄晋鹏.丁坝群和顺岸坝组合工程促淤效果研究［J］.海洋工程，1985，3（1）：15－23.

［7］The Coastal Zone and Tidal Marsh Resources Comprehensive Survey.Wenzhou experimentsite area report［M］.Shanghai：East China Normal University Press，1981.

全国海岸带和海涂资源综合调查温州试点工作队.全国海岸带和海涂资源综合调查.温州试点区报告文集［M］.上海：华东师范大学出版社，1981.

［8］MARC P，DEAN R G.Prediction of beach planforms and littoral controls［J］.Coastal Engineering，1978，110：1 818－1 837.

［9］WANG Shang－yi，ZHOU Ben－fan.Calculation of coastal sediment rate［J］.Acta Oceanologica Sinica，1991，13（5）：692－702.

王尚毅，周本凡.沿岸输沙率计算［J］.海洋学报，1991，13（5）：692－702.

［10］ISAO I.Nearshore dynamics and coastal processes［J］.WANG Wen－hai translated.Coastal Engineering，1995，14（2）：55－66.ISAO I.海滩地貌及其变化［J］.王文海译.海岸工程，1995，14（2）：55－66.

［11］QIU Jian－li.Shoreline change numerical simulation and equilibrium shore－arc analysis of embayed muddy coast［J］.Oceanologia et Limnologia Sinica，1991，22（4）：369－375

邱建立.港湾淤泥质海岸的岸线变化数值模拟和平衡岸弧分析［J］.海洋与湖沼，1991，22（4）：369－375.

［12］ROBERT S Y，DAVID M B.Discussion of the generalized model for simulating shoreline change（GENESIS）［J］.Journal of Coastal Research，1995，11（3）：875－886.

［13］PRICE W A.Predication changes in the plan shape beaches［J］.Coastal Engineering，1972，72：1 321－1 329.