基于MATLAB的BPNN在变压器故障诊断中的仿真参数研究

2012-05-28华丁剑刘建华杨丽娇

电气开关 2012年3期

华丁剑，刘建华，杨丽娇

(长沙理工大学电气与信息工程学院，湖南长沙 410114)

1 引言

电力变压器作为电力系统安全运行中最重要的设备之一，其故障诊断技术一直是国内外相关学者研究的热点。油中溶解气体分析DGA(Dissolved Gas－in－oil Analysis)是目前电力系统对充油电气设备最常用的一种诊断分析方法，能够有效地发现变压器内部的潜伏性故障。但由于电力变压器结构复杂，其故障原因和故障类型之间存在着模糊性，当油中溶解气体含量随时间发生变化时，传统的比值诊断方法不能准确的反映变压器故障和特征气体之间的关系。因此需要找到一种方便可靠的诊断方法，以提高变压器故障诊断的准确率。

人工神经网络ANN(Artificial Neural Network)具有良好的自适应、并行分布处理能力和容错性，在一定程度上克服了传统比值法编码不足和编码边界过于绝对的缺点，通过选择合理的训练样本，采用有效的训练方法，训练得到一个能够较好反映变压器故障与特征气体之间内在规律的网络，将其用于变压器故障诊断可提高诊断准确率。BPNN(Back－propagation Neural Network)由于具有很强的非线性逼近能力，是目前应用最广的人工神经网络模型之一。

本文介绍了BPNN模型和训练流程，并通过MATLAB人工神经网络工具箱进行仿真，分析和对比了不同参数选择对网络训练效果的影响，建立了基于BPNN的变压器故障诊断模型，并验证了其有效性。

2 变压器油中溶解气体的产生机理与故障关系

油和纸是目前油浸式电力变压器的主要绝缘材料，在变压器运行过程中，其绝缘油和绝缘纸等有机材料在放电和受热的作用下，会逐渐老化、分解，产生某些可燃性气体，当发生潜伏性过热或者放电故障时，这些气体的产气量和产气速率也会逐渐增加，直到饱和而析出气泡，使油的绝缘程度降低。由于对于判断油浸式电力变压器内部故障有价值的气体是甲烷(CH4)、乙烷(C2H6)、乙烯(C2H4)、乙炔(C2H2)、氢气(H2)、一氧化碳(CO)和二氧化碳(CO2)，因此把这些气体称为特征气体，而把前四种气体含量的总和称为总烃，通过研究油中溶解的特征气体含量便可发现并判断变压器内部存在着的故障。

3 ANN中的BPNN模型

3.1 ANN简介

3.1.1 基本模型

人工神经网络的基本单元是神经元，其模型如图1所示。

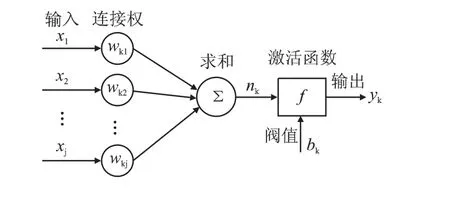
图1 神经元模型

该模型包含了三个基本要素:(1)一组连接，连接强度由各连接上的权值表示;(2)一个求和单元，用于求各个输入的加权和;(3)一个激活函数，起非线性映射作用。用数学公式表达出来如式(1)所示。

式中:x1，x2，……，xj为神经元 k 的输入，wk1，wk2，……，wkj为神经元k的权值，nk为线性求和结果，bk为阀值，f为激活函数，yk为神经元k的输出。

3.1.2 工作原理

人工神经网络的工作过程主要由两个阶段组成:一是工作期，此时各连接权值固定，计算单元的状态变化，以求达到稳定状态;二是学习期(自适应期或设计期)，此时各计算单元状态不变，各连接权可修改。

3.2 BPNN模型

3.2.1 BP网络结构

在众多的ANN模型中，多层前馈网络的反向传播(BP)算法由于良好的模式分类能力，非常适合于变压器故障诊断方面的模式识别问题。BP网络由输入层、隐含层和输出层组成，其中隐含层可以是一层或多层，其结构如图2所示。

图2 BP神经网络结构图

3.2.2 BP学习算法

BP学习算法是一种有监督的学习过程，它是根据给定的样本对(输入、输出)来进行学习，并通过调整网络连接权值和阀值来实现学习的效果。就整个神经网络而言，一次学习过程由输入数据的正向传播和误差的反向传播两个子过程组成。首先将学习样本从输入层输入，经隐含层处理，在输出层得到相应结果，按照实际结果和期望结果误差最小的原则，从输出层到隐含层再到输入层逐层修改连接权值，如此反复，直到学习样本的结果误差在允许误差范围之内或者网络达到了一定的训练次数，则学习过程结束。

假设三层BP网络，输入层节点，隐含层节点，输出层节点，输入层与隐含层之间的网络权值为，隐含层与输出层之间的网络权值为，当输出层的期望值为时，可以得到:隐含层节点输出为:

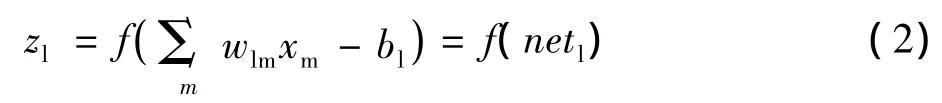
输出层节点输出为:

输出层节点误差为:j

3.2.3 BP算法的学习流程

BP算法的学习流程图如图3所示。

图3 BP算法的学习流程图

(1)对连接权值(包括阀值)初值的设置，初值的设置对网络的收敛性影响较大;

(2)输入学习样本对;

(3)对每个输入样本进行计算输出值;

(4)计算输出层结果的整体误差E，若满足要求则结束，若不满足，则进行(5);

(5)反向计算输出层和隐含层各单元的一般化误差;

(6)分别调整输出层到隐含层和隐含层到输入层的连接权值;

(7)返回(3)，根据新的连接权值进行正向计算，直到E满足要求结束。

4 基于BPNN的变压器故障诊断模型

4.1 学习样本的收集

学习样本的选取是否合适对BP网络的效果至关重要，差的学习样本不但会导致BP网络的错误映射关系，而且可能使得整个网络的学习过程不收敛，因此，在选取学习样本的一般原则是:样本应该尽可能体现输入输出关系，能起“以点带面”的作用;样本最好能提供BP网络各种情况下的输入，并给出相应的期望输出;样本中各故障的百分比应该和实际变压器故障发生的比率相当。

基于上述原则，本文根据实际统计数据选取能反映各种变压器故障类型而又不冗余的36组故障数据作为学习样本，另外收集的10组数据作为检验样本。

4.2 输入、输出模式的确定

网络输入层的节点数就是一个模式所包含的特征量数。考虑到CO、CO2分散性较大，来源较多且现场获得的数据中常有缺失，故选取五种特征气体H2、CH4、C2H6、C2H4、C2H2作为输入特征量，这样网络输入层节点数就为5，为保证网络的收敛性，这里将输入数据作归一化处理，即将各种特征气体占5种气体含量总和百分比作为BP网络的输入向量，所有输入量的取值在0～1之间。

网络输出层的节点数根据待分类的模式数来确定。与比值法类似，将变压器的故障类型分为中低温过热(LH)、高温过热(HH)、高能量放电(HD)、低能量放电(LD)四种，这里将正常情况即无故障也作为一种类型，那么整个网络的输出层的节点数就为5。以二进制形式来表示不同故障类型的输出结果，1表示故障，0表示无故障，如标准高温过热(HH)的输出是［00100］T。

4.3 隐含层的设计

隐含层是实现特征空间到故障空间非线性映射的桥梁，在整个BP网络中起着非常重要的作用。在不限制隐含层节点数的情况下，只含一个隐含层的BP网络可以实现任意非线性映射，对于有限个输入模式到输出模式的映射，并不需要无限个隐含层节点，节点过多会导致学习时间过长;节点太少使得网络容错性差，因此，一般确定隐含层的节点数按经验如式(5)所示。

式中，L为最佳隐含层节点数，M为网络输入层节点数，N为网络输出层节点数，a为一个1～10之间的数。结合本文选取的M=5，N=5，那么L取5～13之间的一个数，因此在同样的网络参数下，设计一个隐含层神经元数目可变的BP网络，通过网络训练误差和训练次数及收敛性的对比，确定最佳的隐含层神经元个数，各个神经元的网络训练结果如表1所示。

表1 网络训练结果比较

4.4 传递函数的选择

对数S型传递函数(logsig)用于将神经元得输入范围(－∞，+∞)映射到(0，+1)。对数S型传递函数是可微函数，因此很适合用于BP算法训练神经网络，其数学表达式为:

其图像如图4所示。

图4 logsig图像

4.5 训练函数的选择

本文采用MATLAB7.0中的ANN神经网络工具箱对模型进行仿真，在MATLAB中，统一由train函数来完成对神经网络的训练。训练函数的选择对于网络的误差和训练时间有着很大的影响，选择越合适的训练函数就越能降低网络的误差和训练时间。本文在保证其他网络参数都相同的前提下，对网络的训练函数依次取traingdm(基于动量BP算法)、traingdx(基于学习率可变的BP算法)、trainrp(基于弹性BP算法)、trainlm(基于LM算法)、trainscg(基于SCG算法)进行对比，仿真结果如下:

图5 traingdm函数

图6 traingdx函数

图7 trainrp函数

图8 trainlm函数

图9 trainscg函数

通过对比可以得出，综合网络收敛性、训练误差和训练时间3个方面，trainrp函数表现的最好，因此本文网络的训练函数采用trainrp。

4.6 网络验证和仿真结果

收集到的验证样本数据如表2所示。

表2 验证样本数据

将十组数据归一化处理后添加到本文网络模型的输入数据，在simulate项中选择其作为Inputs，在Outputs中设定好仿真输出 network1_outputs(1)，点击Simulate Network选项，那么在 Network/Data Manager界面中的Outputs选项中就会出现network1_outputs(1)，选中它并点击View查看仿真结果为:

［1 1 5.6089e－007 1.8761e－016 1.8671e－133 6.8916e－124 7.0835e－012 1.2094e－006 2.6625e－130 2.3851e－091;

0.00055733 0.0016355 0.99999 0.99959 7.6446e－034 6.4013e－024 1.4962e－008 5.8667e－008 2.071e－041 3.3686e－031;

9.5537 e－041 1.1901e－038 2.3878e－027 1.5079e－005 1 1 7.7884e－018 5.4064e－029 2.5797e－032 1.9108e－011;1.3968e－007 2.1824e－009 2.7129e－014 6.2909e－013 2.761e－013 1.303e－019 1 0.99999 1.6107e－006 0.00016548;

8.9092 e－012 1.9099e－013 2.4597e－021 2.3734e－032 1 5.3035e－045 6.0868e－056 1.184e－048 0.98438 0.99916］

仿真结果与实际结果对比如表3所示。