混响空时协方差矩阵的两种计算方法比较与分析

吕 维, 王志杰, 李建辰, 王明洲, 胡 桥



混响空时协方差矩阵的两种计算方法比较与分析

吕 维1,2, 王志杰1, 李建辰1,2, 王明洲1,2, 胡 桥1,2

(1. 中国船舶重工集团公司第705 研究所, 陕西 西安, 710075; 2. 水下信息与控制重点实验室, 陕西 西安, 710075)

协方差矩阵的计算是讨论空时自适应处理（STAP）的基础, 本文主要对协方差矩阵的两种计算方法: 适合理论研究的导向矢量合成方法和符合工程实际的直接阵列数据域方法进行了比较和分析。讨论了这两种方法的计算原理, 以及各自的应用背景; 比较了两种方法的计算结果在混响协方差矩阵形式、特征值、功率谱以及改善因子上的不同。仿真结果表明, 两种计算方法有明显差异, 直接阵列数据域方法对分析其在空时自适应处理理论中的应用提供了更准确的理论基础。

理论导向矢量合成; 直接阵列数据域; 混响协方差矩阵; 空时自适应处理

0 引言

陕西省科学技术研究发展计划(No.2010KJXX-09) 混响是鱼雷自导系统主动工作时特有的干扰, 在浅海环境下界面混响影响尤为严重, 它直接影响鱼雷自导系统主动回波的信号检测能力。因此根据混响特性研究抗混响的信号处理方法具有十分重要的意义。在鱼雷自导工作过程中, 由于鱼雷的运动速度较高, 不同方位角对应的混响具有不同的多普勒频移, 使得混响的空时2D谱在相对较大的范围内扩展开, 具有空时2D耦合特性。利用运动平台混响场的空时结构特性可以有效地进行混响抑制, 近年来空时自适应处理[1]在雷达杂波(混响)抑制中得到了成功的应用, 并有了如DOSAR, DERA, APY-6和空基动目标检测雷达(RADARSAT-2)等一些实用系统。

在进行空时自适应理论研究时, 混响协方差矩阵的计算是关键的步骤。在雷达及声纳空时应用的相关文献中, 常讨论2种协方差矩阵计算方法: 一种是理论导向矢量合成方法[2-6]; 另外一种是直接阵列数据域计算方法。为了理论研究方便, 大多数文献都采用第1种方法, 并在此基础上讨论空时自适应处理的相关问题。但是, 在应用中第1种方法并不完全符合工程实际, 而用第2种方法协方差矩阵更接近实际、适合信号处理应用。本文主要讨论了这2种方法的不同, 特别比较了直接阵列数据域计算方法在空时处理中的不同特性, 为空时自适应理论在工程中应用提供了更准确的理论基础。

1 2种协方差矩阵计算方法原理比较

混响空时协方差矩阵的计算是研究空时自适应处理方法的关键步骤。为了研究空时自适应理论, 首先介绍理论导向矢量合成方法及直接阵列数据域计算方法的计算原理。

1.1 理论导向矢量合成方法

在研究空时处理理论的相关文献中[2], 认为单一距离环的混响空时协方差矩阵等于空间各散射单元的空时协方差的均值。即首先计算来自单一距离环上的每个散射单元相对于每个阵元的维空间导向矢量(如式(1))和在单个脉冲内的维时间导向矢量(如式(2)), 得到每个散射单元的空-时导向矢量(如式(3)), 最终计算来自单一距离环上总的散射单元的回波(如式(4))。

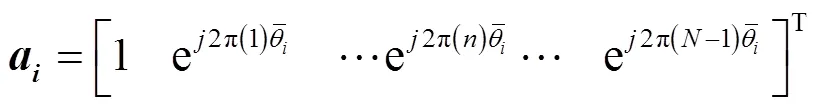
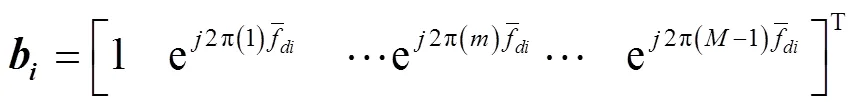
1.2 直接阵列数据域计算方法

这种方法建立在混响阵列回波模型基础上, 其原理是, 首先计算单个脉冲内每个阵元接收的维回波(如式(6)), 根据所有阵元回波(如式(7))形成的×空时2D数据计算协方差矩阵, 如式(8)所示

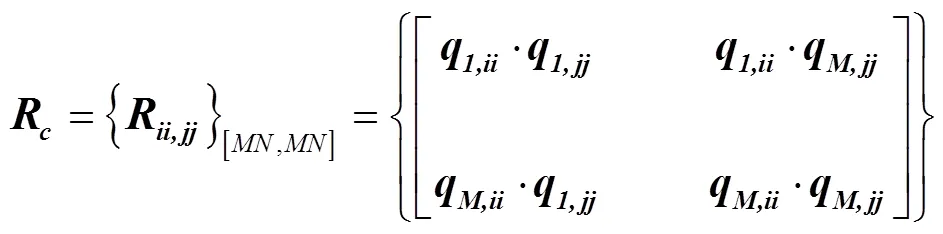
从以上分析可知, 2种空时协方差计算方法有本质的区别。以下分别从协方差矩阵形式、特征值、空时功率谱及改善因子角度分别对2种计算方法仿真结果进行比较。

2 2种计算方法仿真结果比较

2.1 混响协方差矩阵形式

在以往研究前视阵的相关理论中, 为了更清晰的描述空时特点, 往往简化模型, 忽略了基阵指向性的影响。图1为理论导向矢量合成方法计算的协方差矩阵及其矩阵的逆。图2为直接阵列数据域方法计算的协方差矩阵及其矩阵的逆。从2幅图中可以看出, 实际的接收回波数据模型与理论仿真模型的计算结果有明显差异。

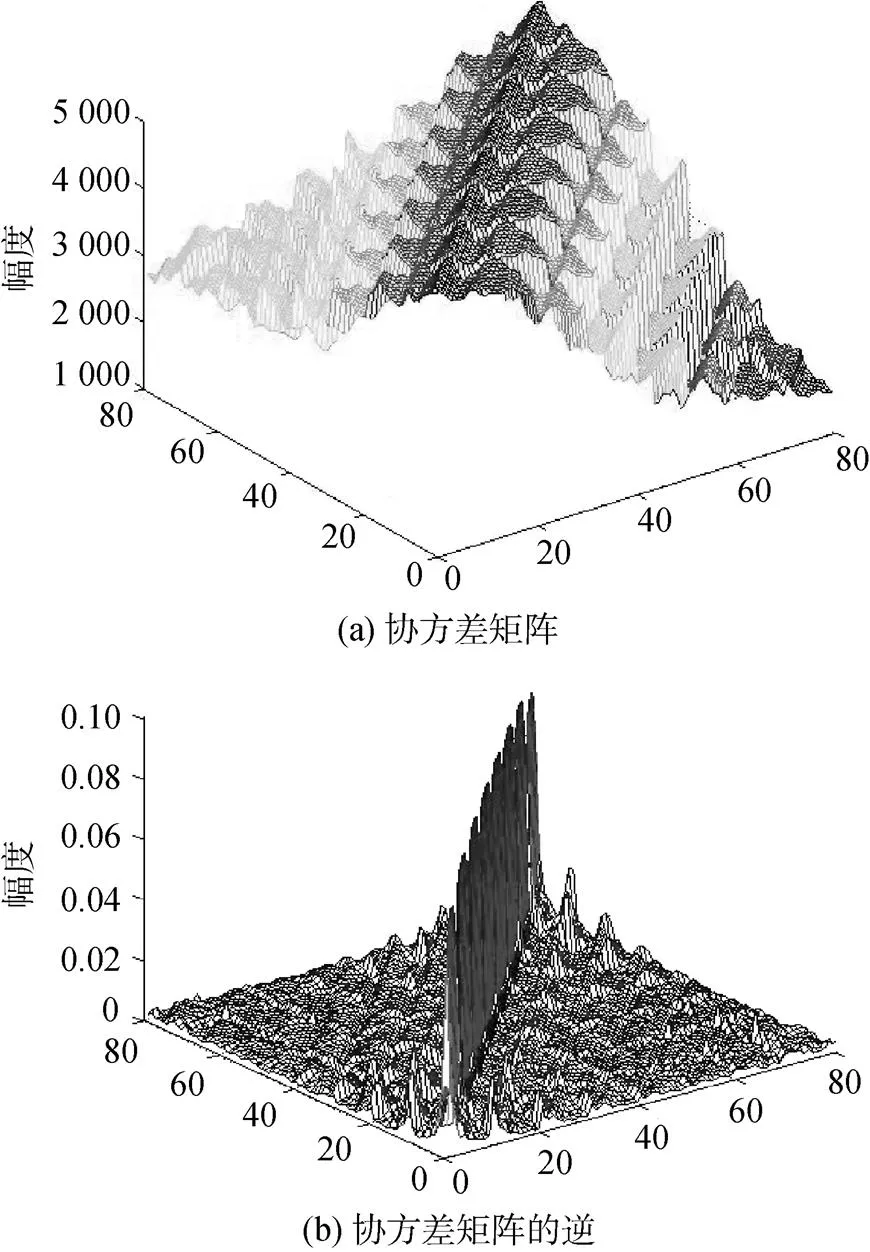
图1 理论导向矢量合成方法计算结果

2.2 协方差矩阵特征值

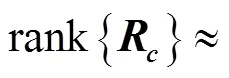
图2 直接阵列数据域方法计算结果

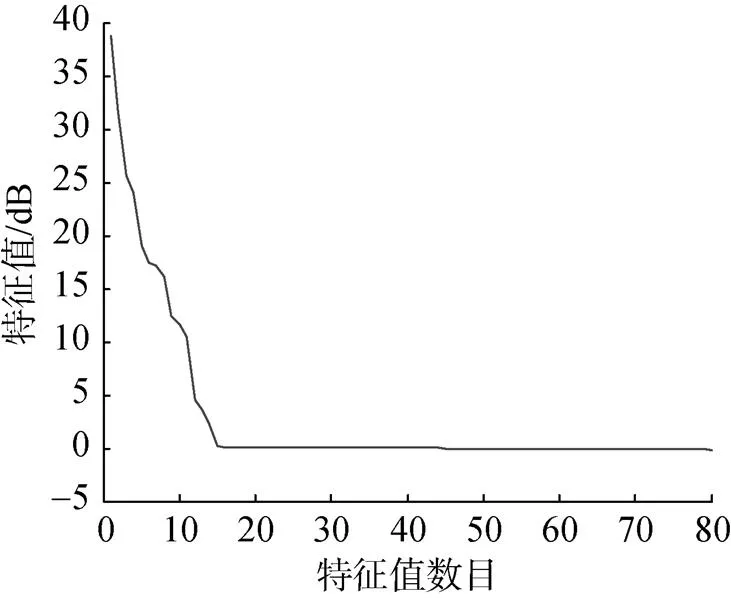
图3 理论导向矢量合成方法计算的特征值

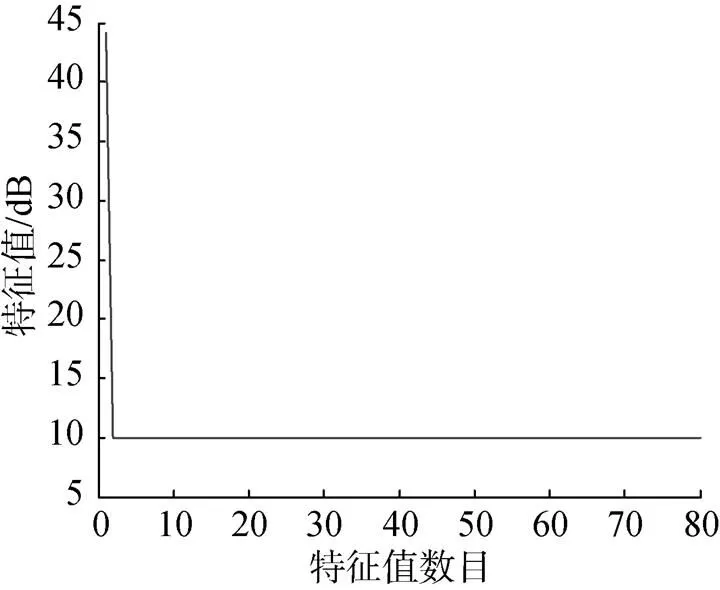
图4 直接数据域方法计算的特征值

2.3 混响空时功率谱

混响空时功率谱反映了混响在空间和时间域上的分布规律, 其计算公式如式(9)所示。图5为按照理论导向矢量合成方法计算的混响功率谱, 这与文献[1]中的计算结果相符, 即混响的空间和时间归一化频率成圆弧形。但实际阵列接收数据与计算结果却有所差异, 如图6所示。

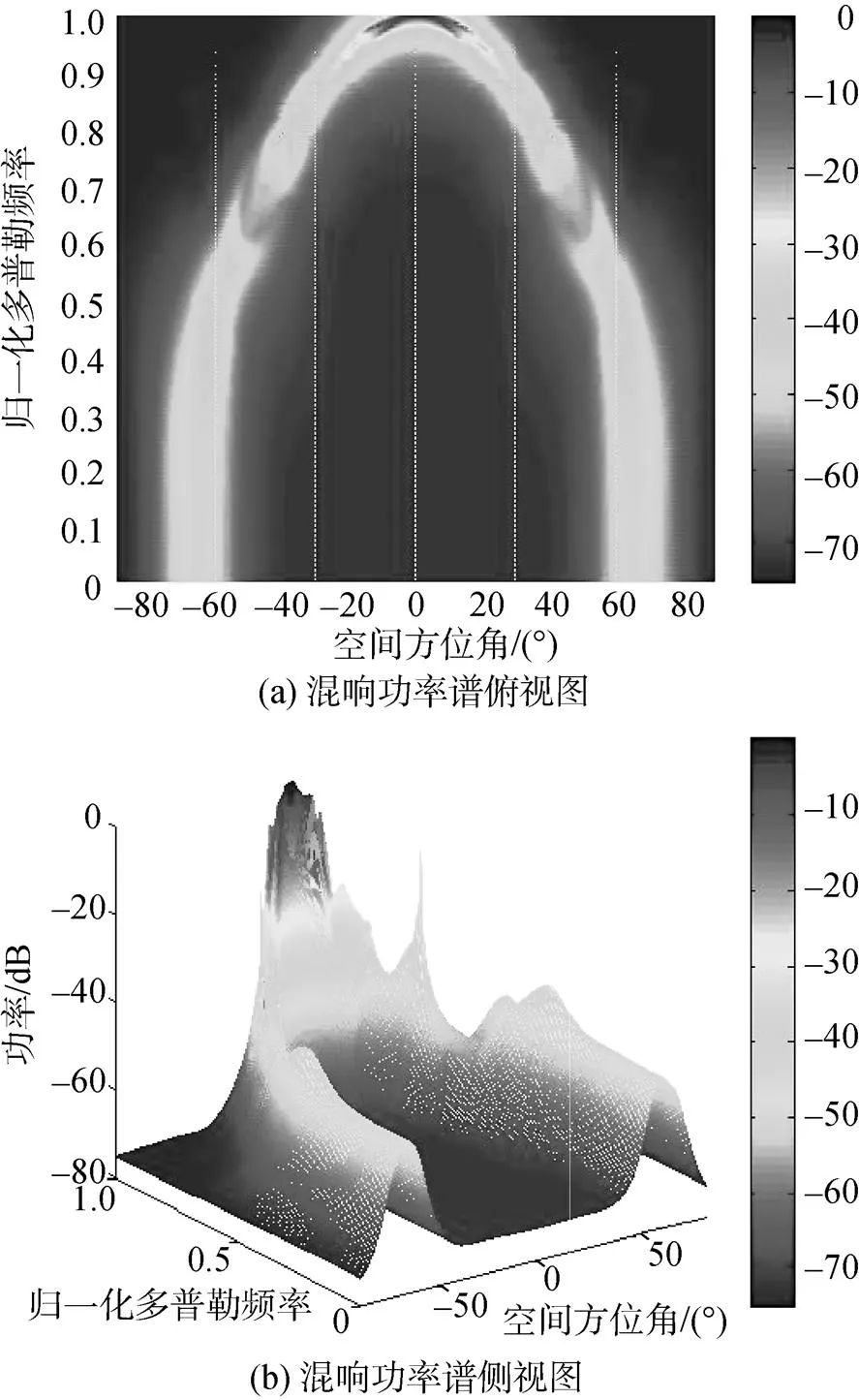
图5 理论导向矢量合成方法计算混响功率

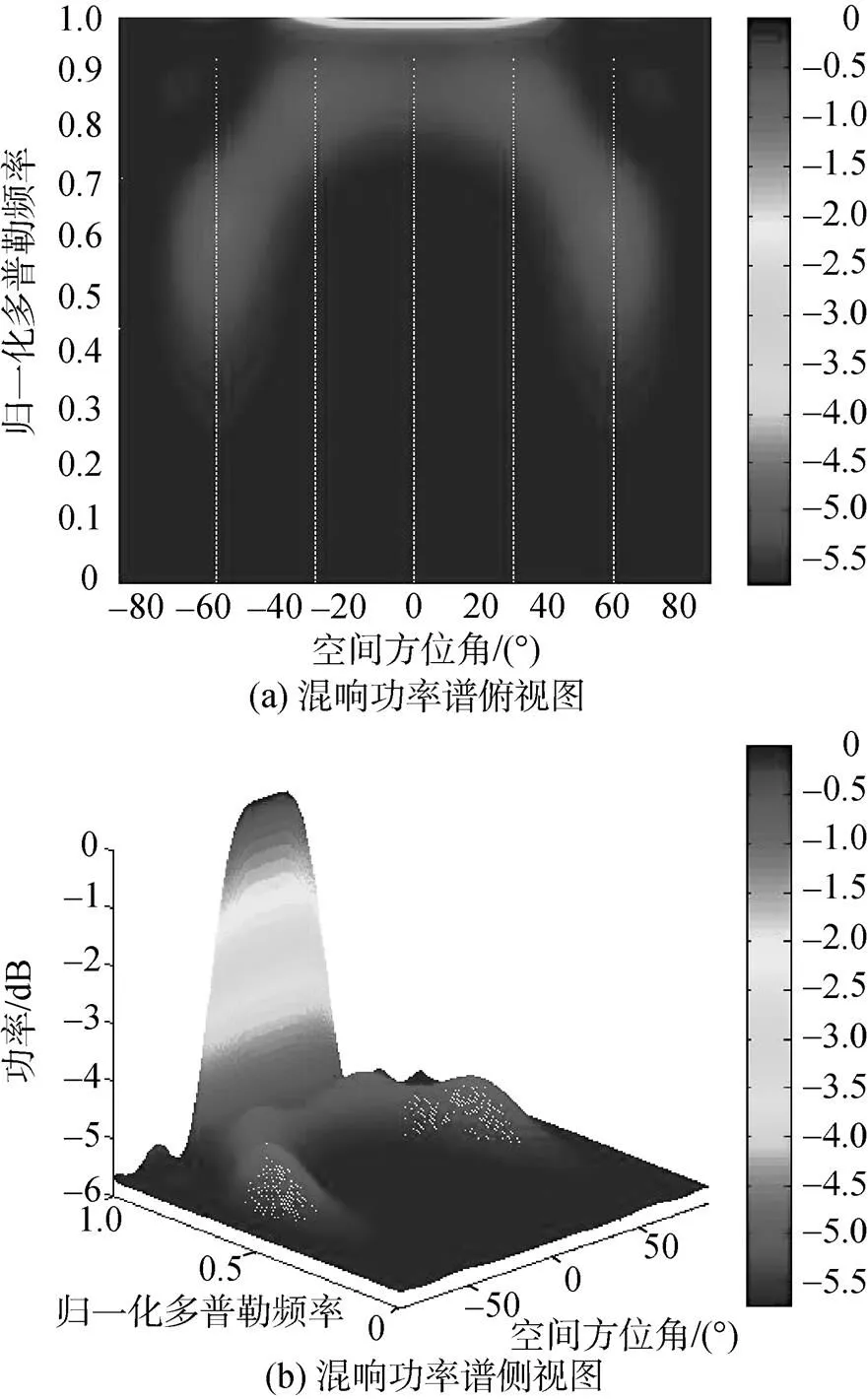
图6 直接数据域方法计算混响功率谱

正如2.2节中分析的, 每个阵元接收的回波都是各自对空间所有散射单元回波的叠加, 最终计算的空时谱在空间上不再完全按照圆弧形分布, 并且在空间上有所扩展。

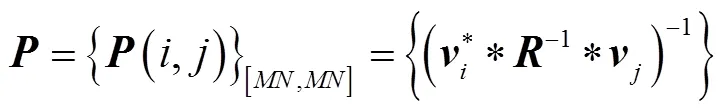
2.4 改善因子

改善因子(improvement factor, IF)是判断空时处理效率的一个标准, 按照空时处理相关理论, 改善因子计算公式如式(10)所示, 其中tr为协方差矩阵的迹。图7为理论导向矢量合成方法计算的改善因子, 从图中可看出, 其结果符合空时理论结果(因为空间角度与归一化多普勒关系是一个半圆, 即两个空间角度对应一个归一化多普勒, 因此图7中的改善因子实质是双边空间角度的叠加结果)。图8为直接数据域方法计算的改善因子, 从图中可以看出, 因为考虑了散射单元内部波动使得对于正、负双边方位角改善因子不同, 这也反映了实际工程的特点, 另外参照2.3节中各自功率谱结果, 改善因子也符合各自特征。

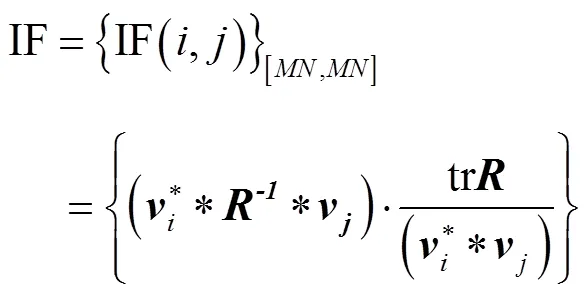
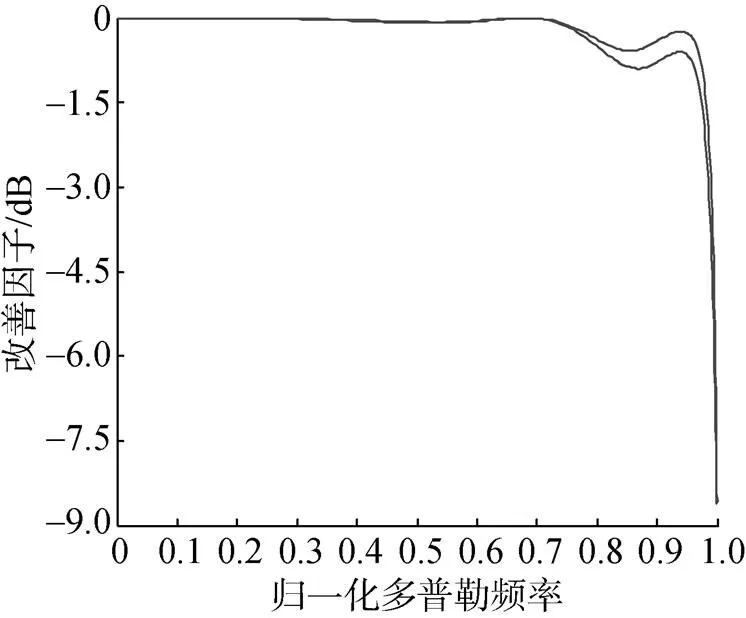
图8 直接数据域方法计算改善因子

3 结束语

空时自适应处理在声纳方面的应用受到越来越多的关注, 以往的理论研究中大多为了简化模型, 采用理论导向矢量合成方法计算协方差矩阵, 这种方法适合于理论分析, 它的结论在某些程度上反映了混响的空时特征, 但这种计算方法并不完全符合实际工程应用。本文采用直接数据域方法计算协方差矩阵, 并讨论和比较了两种协方差矩阵计算原理以及各自计算结果的差异。通过仿真分析可知, 直接数据域方法在计算混响协方差矩阵的形式、特征值、功率谱以及改善因子上与理论导向矢量合成方法有明显的差异, 且直接数据域方法计算的协方差矩阵更接近实际, 适合信号处理应用。因此, 采用直接阵列数据域计算方法在空时处理中的不同特性, 为空时自适应理论在工程中应用提供了更准确的理论基础。

[1] Richard K. Principles of Space-time Adaptive Processing[M]. London: The Institution of Electrical Engineers, 2002.

[2] Guerci J R. Space-Time Adaptive Processing for Radar[D]. 2003 Artech House, INC 685 Canton Street Norwood, MA 02062: Chapter 3, 2003.

[3] 赵申东. 主动声纳空时自适应处理方法研究[D]. 武汉: 海军工程大学, 2008.

[4] 詹昊可, 蔡志明, 苑秉成. 浅海混响扩展的空时2D分布与混响抑制[J]. 鱼雷技术, 2009, 17(2): 29-32.

Zhan Hao-ke, Cai Zhi-ming, Yuan Bing-cheng. Space-Time Two-Dimensional Distribution of Reverberation in Shallow Water and Anti-Reverberation[J]. Torpedo Technology, 2009, 17(2): 29-32.

[5] 詹昊可, 蔡志明, 苑秉成. 一种共形阵主动声纳空时自适应混响抑制方法[J]. 声学技术, 2007, 26(3): 488-492.

Zhan Hao-ke, Cai Zhi-ming, Yuan Bing-cheng. Space-time Adaptive Reverberation Suppression in Active Conformal Sonar of Torpedo[J]. Technical Acoustics, 2007, 26(3): 488- 492.

[6] 何飞, 蒋冬初. 一种全谱域的机载前视阵雷达杂波补偿方法[J]. 计算机工程与应用, 2010, 46(23): 138-140.

He Fei, Jiang Dong-chu. Whole Spectrum Clutter Compensation Method for Forward Looking Airborne Radar[J]. Com­puter Engineering and Applications, 2010, 46(23): 138-140.

Comparison and Analysis of Two Calculation Methods of Space Time Covariance Matrix for Reverberation

LÜ Wei1,2, WANG Zhi-jie1, LI Jian-chen1,2, WANG Ming-zhou1,2, HU Qiao1,2

(1. The 705 Research Institute, China Shipbuilding Industry Corporation, Xi¢an 710075, China; 2. Science and Technology on Underwater Information and Control Laboratory, Xi¢an 710075, China)

Calculation of covariance matrix is a basis for space time adaptive processing(STAP). Two methods for calculating reverberation covariance matrix, the steering vector synthesis method adapting to theoretical analysis and the direct array data domain method adapting to engineering, are discussed in this paper. The principles and applications of the two methods are analyzed, and their calculation differences in the form, eigenvalue, power spectrum and improvement factor of reverberation covariance matrix are compared. Simulation results illustrate that the two methods are obviously different, and the direct array data domain method lays the more exact theoretical foundation for its application to STAP.

theoretical steering vector synthesis; direct array data domain; reverberation covariance matrix; space time adaptive processing(STAP)

TJ630.34; TN957

A

1673-1948(2012)4-0251-05

2011-10-26;

2011-11-10.

陕西省科学技术研究发展计划资助项目(2010KJXX-09).

吕维(1984-), 女, 在读博士, 主要研究方向为水下信号处理.

(责任编辑: 杨力军)