含横向裂纹Jeffcott转子刚度及动力学特性研究

杨 丹，甘春标，杨世锡，熊 炘

含裂纹转子的非线性动力学特性主要受转轴的时变刚度的影响。现有的横向裂纹刚度轴模型有两种:全开裂纹模型和开闭裂纹模型。全开裂纹模型是指在转子运行过程中，裂纹始终受到拉应力作用或者不容易闭合，因此裂纹是常开的。开闭裂纹模型是指在转子运行过程中，裂纹时而张开，时而闭合，时而半开半闭，其综合考虑了裂纹截面的三种状态，因此更能反映实际转子的运行情况。国内外学者提出了多种模型来描述裂纹的开闭规律，如方波模型［3］、余弦模型［4］和高朱模型［5］，以上这些模型近似地模拟了裂纹的开闭规律，确定刚度的方式比较简单。Dimarogonas等［6］提出了借助断裂力学理论来计算裂纹轴的附加柔度，在理论上分析了裂纹转子的开闭规律。林言丽等［7］基于中性轴理论，假设重力占优，根据截面的平衡条件得到了适用于低速运行转子的裂纹刚度的数值解。王宗勇等［8］在裂纹处于全开和半开半闭状态时，中性轴依然经过完好裂纹截面形心的假设下，推导了基于中性轴理论的开闭裂纹刚度解析解。

本文以两端刚性支承的Jeffcott转子系统为研究对象，首先参考王宗勇等在文献［8］中给出的裂纹模型解析解，同时考虑裂纹张开区域对截面中性轴位置的影响［7］，利用中性轴理论模拟了裂纹的开闭规律，由裂纹截面的惯性矩与惯性积得到了截面各方向刚度系数数值解。然后建立了不依赖于重力占优假设的运动微分方程，借助时域波形图、频谱图、相轨迹图、轴心轨迹图，得出系统动力学特性随裂纹深度、转速的变化规律。

1 系统动力学方程

本文研究的含横向裂纹Jeffcott转子模型如图1所示，该Jeffcott转子模型两端刚性支承，在转轴中心处有一质量为m，阻尼为c的圆盘，在转轴靠近圆盘处有一条横向弓形裂纹。支撑连线垂直于xy平面，且经过原点，x轴垂直向下，y轴为水平方向。图2给出了开闭裂纹模型示意图，其中:e为质量偏心;o'ρ为转轴的变形方向;o'ξ为裂纹扩展方向，即法向;o'η为裂纹扩展垂直方向，即切向;ψ为转子的涡动角;θ为自转角;φ=θ－ψ为裂纹参考角，即转涡差角;β为不平衡量与裂纹方向之间的夹角;α为裂纹角。

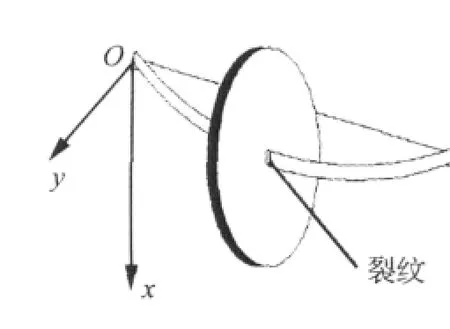
图1 含横向裂纹Jeffcott转子Fig.1 The Jeffcott rotor with the cross crack

图2 开闭裂纹模型示意图Fig.2 Schematic diagram of the switching crack model

仅考虑转子的横向振动，忽略裂纹对系统质量和阻尼的影响，利用Lagrange方程建立系统在图2所示的直角坐标系xoy中的动力学方程［9］:

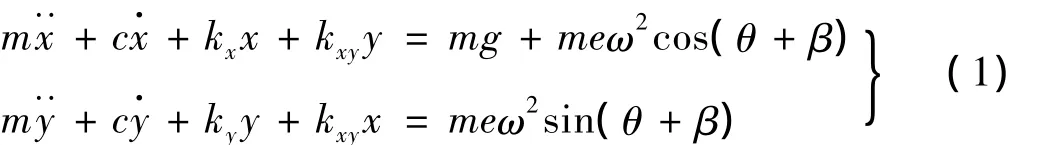
式(1)中:m为圆盘的质量，c为圆盘的阻尼系数，kx、ky、kxy为两横向刚度及耦合刚度系数，e为圆盘的偏心量，ω为转轴自转角速度。令=ω/Ω，θ=ωτ/Ω+θ0，可得含裂纹转子系统运动微分方程的无量纲形式如下:

式(2)中:kx、ky、kxy分别为:

（1）施工准备。基层施工前应对相关机具设备进行检测，确保性能完好，可满足施工需求；应对下承层路基进行相应处理，清扫杂物后使用22t钢轮压路机进行碾压，对干燥松散部分应进行适当洒水，碾压完成后应检测其弯沉值，符合设计与规范要求后方可进行基层施工[3]。

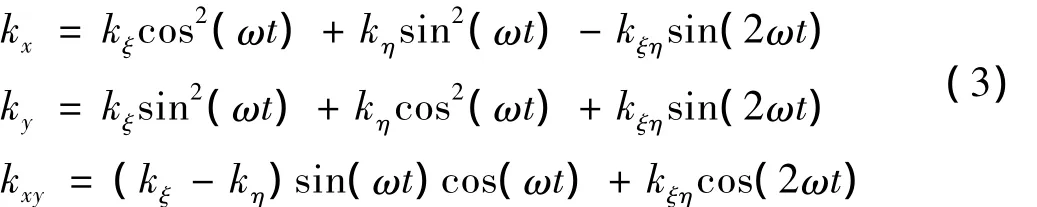
式(3)中:kξ为裂纹法向刚度系数，kη为切向刚度系数，kξη为耦合刚度系数。影响开闭裂纹截面刚度系数的是裂纹张开区域的面积与形状，本文基于材料力学中性轴理论［10］，在文献［8］的基础上考虑裂纹张开区域对中性轴位置的影响，利用求得的中性轴与裂纹的相对位置确定裂纹的张开、闭合区域，借助截面惯性矩建立一种更为准确的开闭裂纹转子刚度模型。

2 开闭裂纹刚度模型的研究

2.1 基于中性轴理论的裂纹模型

在转子运行过程中，裂纹截面的拉伸区与压缩区随着应力场分布的变化不断变化，引起裂纹的张开、闭合交替变化，从而导致裂纹截面的刚度不断发生变化。中性轴［10］是平面弯曲和斜弯曲时横截面和应力平面的交线，是截面拉压区域的分界线，如图3所示，位于中性轴上方的裂纹截面处于压应力区，位于中性轴下方的处于拉应力区。文献［7］基于中性轴理论与截面的平衡条件得到了裂纹截面刚度的数值解，但是该刚度模型假设重力占优，仅适用于低速运行的转子。文献［8］基于裂纹处于全开或半开半闭状态时，截面的中性轴依然经过完好截面形心的假设，给出了裂纹截面刚度的解析解。但是由于裂纹的存在，裂纹在全开或半开半闭状态下，中性轴不通过完好截面形心［7］，因此，文献［8］在确定裂纹张开、闭合区域时会有不太准确的情况。本文在不考虑裂纹端应力集中的假设条件下，当裂纹处于全开或半开半闭状态时，考虑裂纹张开区域对裂纹截面中性轴位置的影响，得到偏离完好截面形心一定距离的中性轴，如图3所示。o'l是完好截面的中性轴，由于裂纹的存在，中性轴常常偏移圆心o'一定的距离，位于中性轴上方的部分裂纹面处于压应力区，处于闭合状态，如图3中阴影部分，位于中性轴下方的部分裂纹面处于拉应力区，处于张开状态。我们需要确定中性轴的位置来确定裂纹的张开、闭合区域，在截面上找到一条方向垂直于转轴涡动方向的中性轴，使其满足截面的轴向力平衡条件［10］:

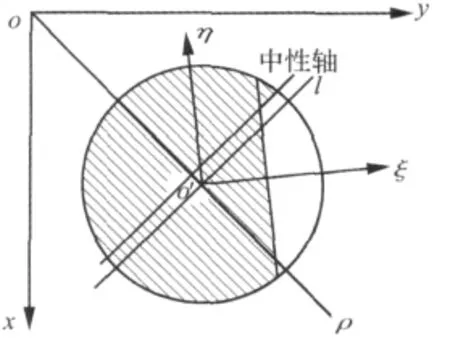
图3 裂纹截面中性轴位置示意图Fig.3 Schematic diagram of the neutral axis position on the crack section

式(4)中:N是裂纹截面的轴向合力，σ是截面上任意一点正应力，A是图3中阴影部分的面积，即截面的无裂纹区域加上裂纹的闭合区域。根据材料力学理论［10］，假设不考虑应力集中，纯弯曲时距离中性轴为y的任意一点的正应力为:

式(5)中:y的正负号取决于该点位于拉应力区还是压应力区，E是弹性模量，ρ是弯曲半径。E/ρ是常量，故由式(4)、式(5)知，必须有横截面(图3阴影部分)对中性轴的静矩等于零［10］，即:

由式(6)确定对应转涡差角下裂纹截面的中性轴位置，从而确定裂纹张开、闭合区域，然后通过求解截面惯性矩得到相应的刚度。

2.2 刚度求解

首先，由式(6)可得不同转涡差角时中性轴相对圆心o'的距离，图4是裂纹角分别为π/6、π/4、π/3时中性轴相对圆心的距离随着转涡差角的变化。由图4可知:中性轴相对圆心的距离随着转涡差角以2π为周期波动，裂纹开闭过程和闭开过程关于转涡差角以π对称，裂纹全闭的转涡差角范围随着裂纹加深而缩小。在裂纹角较小时(α=π/6)，中性轴移动距离接近于0，说明此时中性轴靠近圆心;当裂纹角较大时(α=π/3)，中性轴有着非常明显的偏移。

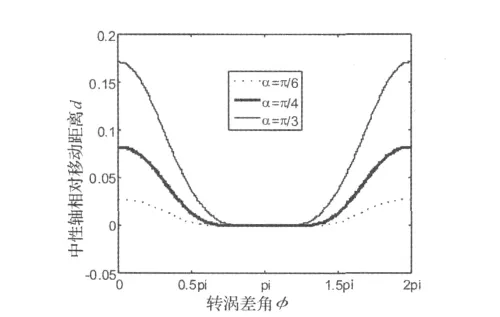
图4 中性轴相对圆心的距离Fig.4 Relative distance between the neutral axis and the centre of circle

中性轴是裂纹截面拉压区域的分界线，截面的拉、压应力分布场决定裂纹的张开、闭合区域:当裂纹完全处于拉应力区域时，裂纹处于全开状态;当裂纹完全处于压应力区域时，裂纹处于全闭状态;当裂纹边界线与中性轴相交时，裂纹处于半开半闭状态。因此，在确定了不同转涡差角对应的中性轴的位置后，即可确定相应转涡差角下裂纹的张开、闭合区域，从而确定转子运行过程中，裂纹全开状态、由开到闭过渡状态、全闭状态以及由闭到开过渡状态的转涡差角范围:

全开:(－π/2－Δ+α)～(π/2+Δ－α)

开闭过渡:(π/2+Δ－α)～(π/2+α)

全闭:(π/2+α)～(3π/2－α)

闭开过渡:(3π/2－α)～(3π/2Δ+α)

其中:

表1和表2分别给出了不同裂纹深度时，本文模型和文献［8］模型各个状态对应的转涡差角范围，由于裂纹开闭过程与裂纹闭开过程的对称性，表中仅给出了裂纹全开、由开到闭、裂纹全闭三种状态对应的转涡差角范围。由表可知:随着裂纹角的增大，裂纹全开、全闭状态的转涡差角范围减小，半开半闭过渡状态的转涡差角范围增大。本文模型裂纹全开状态对应的转涡差角范围比文献［8］模型大，半开半闭状态对应的转涡差角范围比文献［8］模型小。

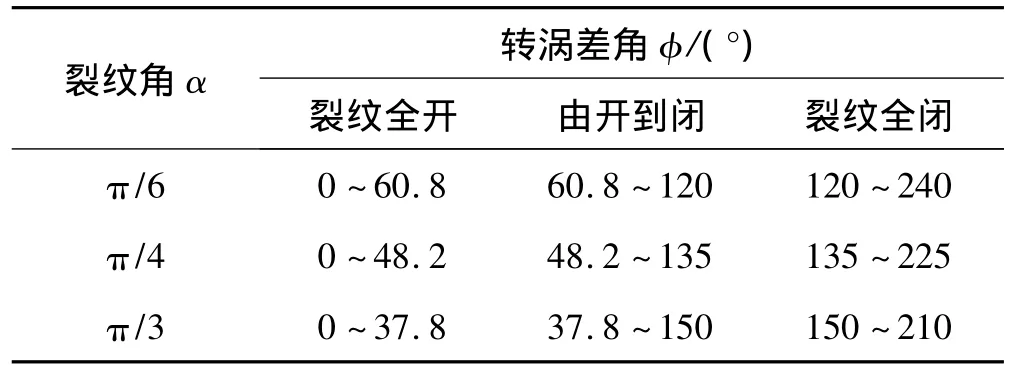
表1 不同裂纹深度下本文模型关于裂纹开闭的转涡差角Tab.1 The present switching crack angle with different crack depth

表2 不同裂纹深度下文献［8］模型关于裂纹开闭的转涡差角Tab.2 The switching crack angle with different crack depth from［8］

由中性轴和裂纹的相对位置确定了裂纹的张开、闭合区域后，即可求得转动坐标系下截面无裂纹区域和裂纹闭合区域对于oη轴和oξ轴的惯性矩及积惯性矩:

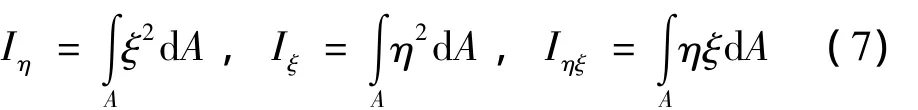
式(7)中，A为图3中阴影部分的面积。

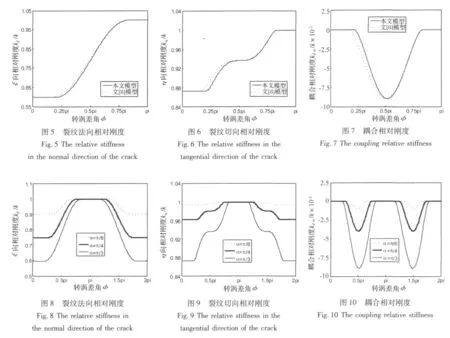
借助截面各方向惯性矩的求解结果，得到裂纹截面各方向的刚度系数。以α=π/3为例，对本文模型和文献［8］模型作对比，由于裂纹开闭过程与闭开过程的对称性，图5～图7给出了转涡差角0～π范围内转动坐标系下的相对刚度系数。由图可知，本文模型较之于文献［8］模型延迟进入半开半闭状态，产生这种情况的原因是文献［8］在裂纹处于完全张开状态与半开半闭状态时，依然假设中性轴通过完好截面形心，而本文依据中性轴的定义，考虑了裂纹张开区域对中性轴位置的影响。当转子转涡差角由37.8°转至90°时，由于本文模型中性轴相较于完好截面中性轴有明显的偏移，本文模型的裂纹法向刚度和切向刚度系数比文献［8］模型大，耦合刚度系数比文献［8］模型小。在其他转涡差角下，本文模型和文献［8］模型各刚度曲线基本重合。

2.3 裂纹深度对截面不同方向刚度的影响

本文模型综合考虑了裂纹全开，过渡和全闭三种状态。图8～图10分别给出了不同裂纹深度时含裂纹截面的裂纹法向、切向与耦合相对刚度曲线。由图可知:裂纹的存在对裂纹法向和切向刚度系数的影响较大，对耦合刚度系数影响较小，并且耦合刚度系数总接近于零值。随着裂纹深度的增加，裂纹对刚度的影响增大，裂纹半开半闭的过渡过程更加明显。不同裂纹深度时，各刚度曲线形状基本一致:法向刚度曲线呈现曲边梯形状，切向刚度呈现五个平台的阶梯形状，耦合刚度呈现对称的半周期正弦曲线形状。

3 稳态响应

为了了解系统的动力学特性，需研究参数变化时系统的各种运动现象。本文采用龙格－库塔法求解无量纲化的非线性振动微分方程，通过数值仿真获得系统在不同参数变化下的振动响应，分析和研究了含裂纹Jeffcott转子的时间历程、响应频谱、相轨迹、轴心轨迹。设定转子系统各参数值为:

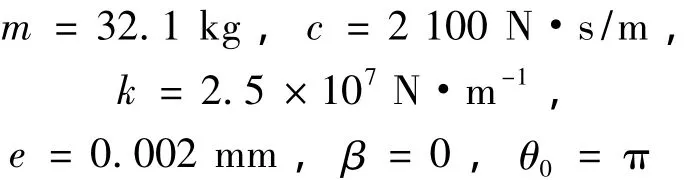
3.1 裂纹深度对振动响应的影响

无裂纹转子系统的一阶临界固有频率为fc=/2π =140.5 Hz。图 11(1)、(2)、(3)行给出裂纹角为 π/6、π/4、π/3时转频f=fc/3=46.8 Hz时系统振动响应的水平方向时域波形图、频谱图、相轨迹图和轴心轨迹图。由图可知:频谱图上包含工频的1倍频、2倍频与3倍频分量，其中3倍频分量较为突出，1倍频分量主要由质量偏心引起，其他分量则主要由裂纹产生。相轨迹图和轴心轨迹图由三条封闭曲线组成。随着裂纹深度的增加，系统响应的高阶谐波分量更加明显，3倍频分量与其他倍频分量的大小差距缩小，裂纹较深时(裂纹角为π/4、π/3)频谱图上出现了相对微弱的4倍频分量，轴心轨迹和相轨迹图也都有着非常明显的变化。

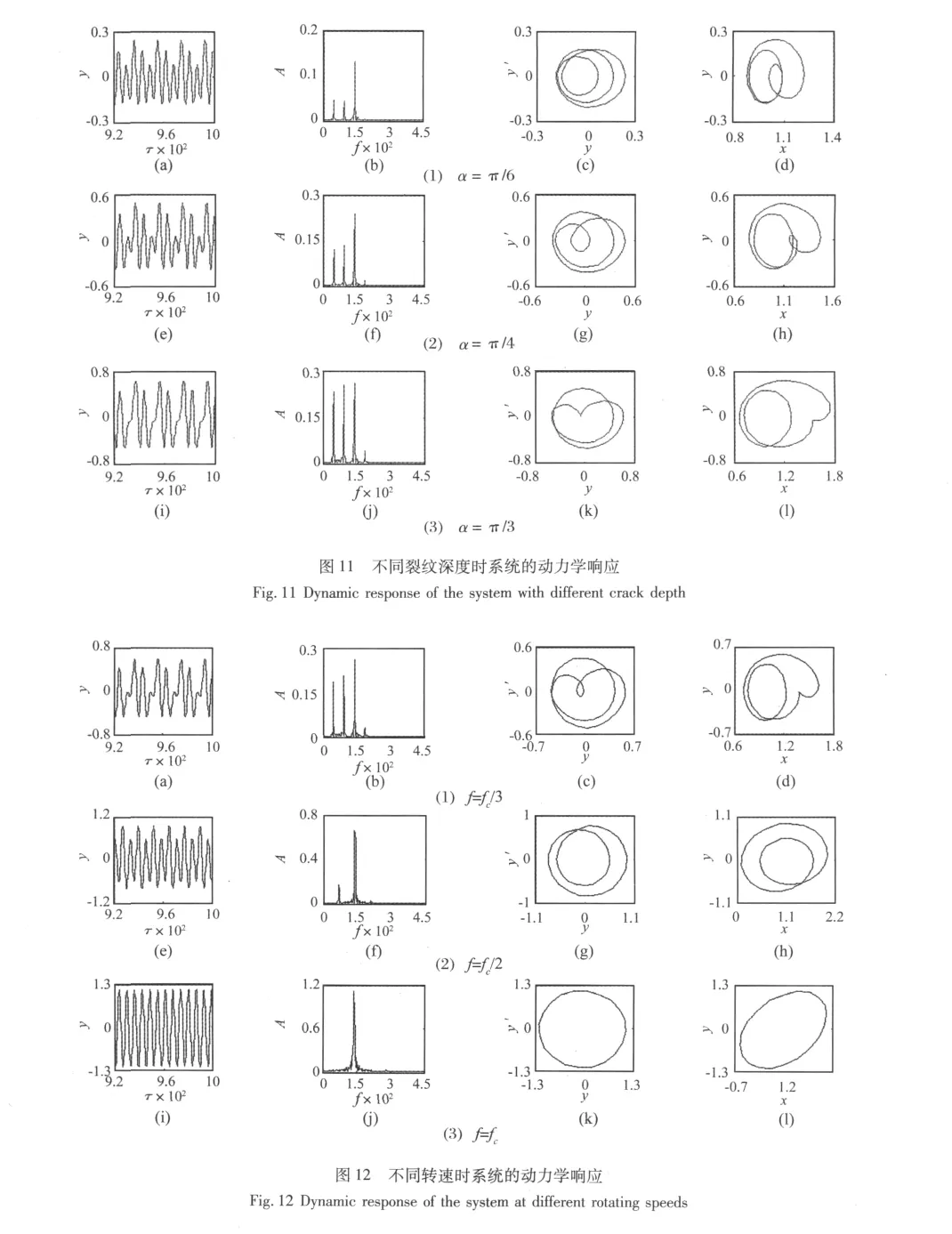
3.2 转速对振动响应的影响

图12(1)、(2)、(3)行给出裂纹角为 0.3π 时转频分别为fc/3，fc/2，fc时系统振动响应的水平方向时域波形图、频谱图、相轨迹图和轴心轨迹图。由图可知，当转频等于一阶临界固有频率的1/3和1/2时:由偏心引起的振动响应较小，还不足以掩盖由裂纹引起的振动响应，因此频谱图上包含比较丰富的高次谐波分量，轴心轨迹图和相轨迹图都呈不同大小的圆圈交叉状。此时由于裂纹的存在，系统的固有频率被激发，出现分数次共振现象，可作为裂纹故障的重要特征。当转频等于一阶临界固有频率时:由偏心引起的振动响应起主导作用，因此转盘的横向振动为转速的同频振动，轴心轨迹图和相轨迹图都呈规则形状。

4 结论

本文根据中性轴理论，研究了不同裂纹深度下裂纹开闭规律和转轴的时变刚度。在此基础上，建立了含横向裂纹Jeffcott转子系统的动力学方程，较详细地讨论了裂纹深度和转速对系统振动特性的影响，得到了如下结论:

(1)考虑裂纹的张开区域对中性轴位置的影响，能更加准确地揭示含裂纹转子转轴刚度的时变特性。裂纹对裂纹截面的法向和切向刚度系数的影响较大，而耦合刚度系数总接近于零值。

(2)随着裂纹深度的增加，裂纹的开闭过渡过程更加明显，系统响应的频谱图趋向复杂，高阶谐波分量更加明显，轴心轨迹和振动响应相轨迹图也都有着非常明显的变化。

(3)当转速等于一阶临界转速的1/3和1/2时，系统的固有频率被激发，出现分数次共振现象。

(4)在转速较低时，由质量偏心引起的振动响应较小，不足以掩盖由裂纹引起的振动响应，故在轴心轨迹图和振动响应相图中，都呈不同大小的圆圈交叉状;在转速较高时，由质量偏心引起的振动响应起主导作用，轴心轨迹图和振动响应相图都呈现规则形状。

［1］Wang C H，Brown M W.Life prediction techniques for variable amplitude multiaxial fatigue［J］. Journal of Engineering Materials and Technology，Transaction of the ASME，1996，118(3):367－370.

［2］Shang D G，Wang D J.Simple approach to the description of multiaxial cyclic stress－ strain relationship［J］.International Journal of Fatigue，2000，22(3):251 －256.

［3］Gasch R.A survey of the dynamic behavior of a simple rotating shaft with a transverse crack［J］.J.Sound and Vibration，1993，160(2):313 －332.

［4］Mayes I W，Mayes I W，Davies W G R，et al.Analysis of the response of a multi-rotor-bearing system containing a transverse crack in a rotor［J］.Journal of Vibration，Acousties，Stress，and Reliability in Design，1984，106:139－145.

［5］高建民，朱晓梅.转轴上裂纹开闭模型的研究［J］.应用力学学报，1992，9(1):108 －112.GAO Jian-min，ZHU Xiao-mei.Study on the model of the shaft crack opening and closing［J］.Chinese Journal of Applied Mechanics，1992，9(1):108 －112.

［6］Dimarogonas A D.Vibration of cracked structures:a state of the art review［J］.Engineering Fracture Mechanics，1996，55(5):831－875.

［7］林言丽，褚福磊.裂纹转子的刚度模型［J］.机械工程学报，2008，44(1):114 －120.LIN Yan-li，CHU Fu-lei.Stiffness models for the cracked shaft of the rotor systme［J］.Chinese Journal of Mechanical Engineering，2008，44(1):114 －120.

［8］王宗勇，林 伟，闻邦春.开闭裂纹转轴刚度的解析研究［J］.振动与冲击，2010，29(9):69－72.WANG Zong-yong，LIN Wei，WEN Bang-chun.Analysisi on stiffness of rotor system with a swiching crack.Journal of Vibration and Shock.2010，29(9):69 －72.

［9］邹 剑，陈 进，蒲亚鹏，等.开闭裂纹转子的建模与弯曲刚度特性研究［J］.振动与冲击，2001，20(4):47－49.ZOU Jian，CHEN Jin，PU Ya-peng，et al.On modeling and bending stiffness properties of rotor with switching crack［J］.Journal of Vibration and Shock.2001，20(4):47－49.

［10］刘鸿文.材料力学［M］.北京:高等教育出版社，2004.LIU Hong-wen. Mechanics of materials［M］. Higher Education Press，Beijing，2004.