苎麻纤维性能与成纱质量的人工神经网络分析

高晓艳，郁崇文*

(东华大学纺织学院，上海 201620)

纱线是由纤维纺成的，因此成纱性能主要取决于纤维性能和纺纱时的工艺参数，但他们之间的关系是复杂的、非线性的，成纱性能的预测是一个很困难的课题。针对这种情况，国内外的学者进行了很多研究，建立了统计模型和人工神经网络模型来根据纤维性能预测成纱性能［1］。李晓峰［3］运用灰色系统分析了苎麻纤维原料品质与成纱品质指标之间的关系;蔡煜东［4］运用神经网络的典型模型— “反向传播”模型，建立了由亚麻纤维的品质预报其成纱质量的连接机制模型。这些研究表明，应用神经网络进行成纱质量预测时输入参数的个数和代表性是影响预测结果准确性的主要因素。因此，本文采用灰色分析和主成分分析法从诸多的输入变量中筛选出几个重要的变量作为神经网络的输入，从而简化神经网络的结构，并使最终的预测结果更准确、稳定。

1 数据准备

本文采用从湖南明星麻业股份有限公司收集到的50组数据建立预测模型，其中40组用于训练网络和建立模型，另外10组用来检验所建模型的预测精度。当纺纱工艺参数相同时，影响成纱质量的主要因素是纤维和半成品的性能。

精梳是苎麻纺中的一个关键工序，该工序能清除麻条中不能适应纺纱要求的短纤维，提高纤维平均长度和整齐度，清除麻条中的麻粒和缠结的纤维，提高麻条中纤维的伸直平行度，所以精梳条的质量对细纱品质有直接的影响。因此本文选用的精干麻和半成品的性能指标为:精干麻束纤维的平均断裂强度 (x1)、精干麻细度 (x2)、精干麻硬条率 (x3)、精梳条的麻粒(x4)、精梳条并丝 (x5)、精梳条重量不匀 (x6)、精梳条重量偏差 (x7)和精梳条回潮率(x8);成纱的性能指标为:成纱强力 (Y1)、成纱强不匀 (Y2)、成纱条干 (Y3)和成纱麻粒(Y4)。

2 主成分分析

主成分分析法可以把多个指标化为少数几个不相关的综合指标，用维数较少的互不相关的主成分来反映原变量的大部分信息［2］。

为了消除不同变量之间量纲的差异，首先用公式 (1)对纤维的性能指标数据X=(X1，X2，…Xp)T进行标准化处理:

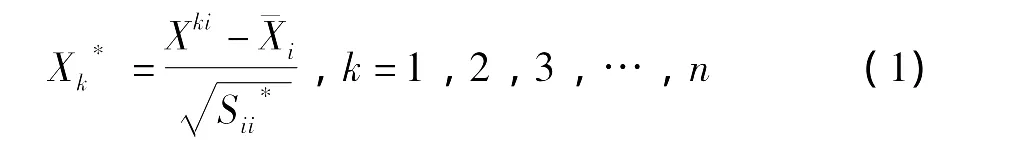
然后计算协相关系数矩阵R的特征值和特征向量 (λ1，e1)，(λ2，e2)，…，(λp，ep)，λ1≥λ2≥…≥λp≥0，根据特征值计算方差贡献率和累计贡献率。第k个主成分的方差贡献率为:λk/，前m个主成分的累计贡献率为:，一般取m＜p。当累计贡献率较大(本文选80%)时，则这些主成分即可大部分地反应原来的p个变量所包含的信息。

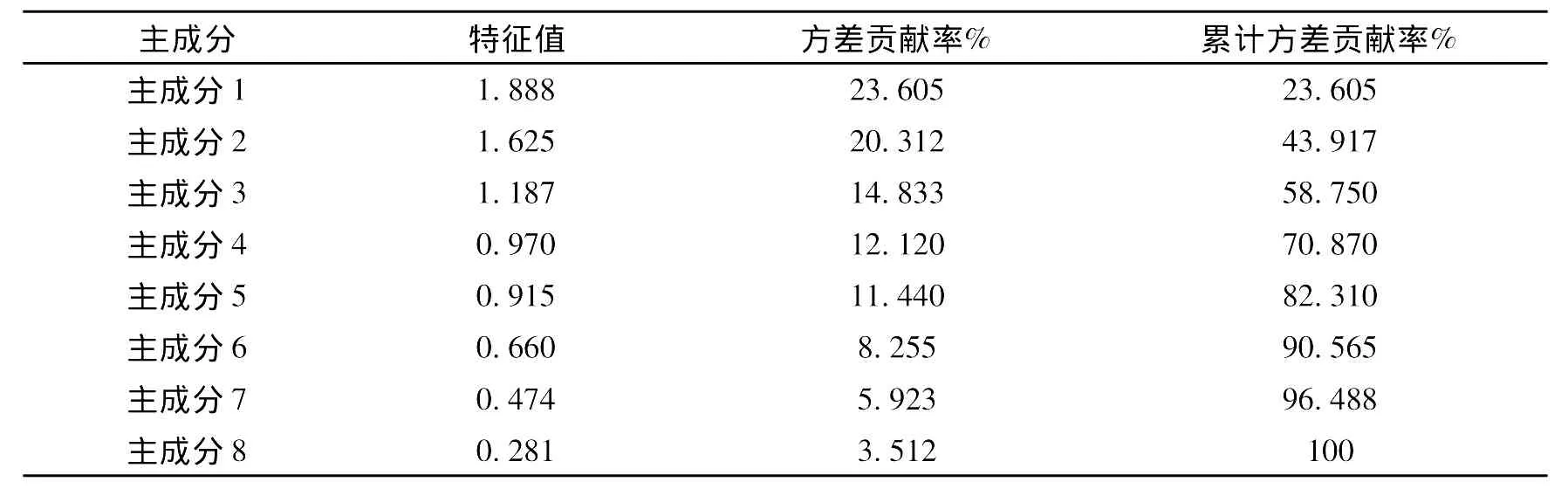
表1 特征值和累计方差贡献率Tab.1 Eigenvalue and cumulative variance contribution rate

关于主成分的个数如何确定，常用的标准有两个:一是按累计贡献率达到一定程度 (如70%或80%以上)来确定m;另一个是先计算p个特征值的均值¯λ，取大于¯λ的特征值个数m。当变量个数p＜20时，大量实践表明，第一个标准容易取太多的主成分，而第二个标准容易取太少的主成分，故最好将两者结合起来使用［2］。本文中¯λ=1，若按¯λ＞1的标准取，只能取前3个主成分，累计贡献率较小，而第4个和第5个主成分的λ=0.970、0.915接近于1，所以综合考虑提取前5个主成分。提取出主成分后，根据公式 (2)计算主成分分值，用计算得到的前5个主成分分值作为神经网络的输入。

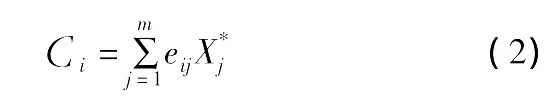
Ci是第i个主成分的分值，eij是对应于特征值λi的特征向量分量。

3 灰色关联分析

灰色关联分析可以通过比较各个因素之间的相似程度来衡量它们之间的关系。苎麻纤维性能对成纱性能有一定的影响，但是这一系统的大部分信息又未知，如纤维各指标对成纱性能指标的影响大小未知，故这一系统为灰色系统，因此可对苎麻纤维性能指标与成纱性能指标进行灰关联分析［5］。

在灰关联分析之前，先对数据进行预处理，以消除原变量的量纲不同、数值差异太大带来的影响，可根据公式 (3)进行规格化处理。

其中，x为纤维和半成品的性能指标，Y为成纱性能指标。

然后根据公式 (4)计算灰色关联系数

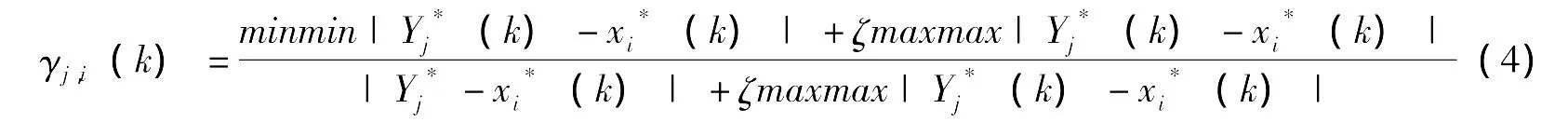
式 (4)中，ζ为分辨系数，ζ∈ ［0，1］，一般选 ζ=0.5;分别为两级最小差和两级最大差。

由于关联系数是点对点的系数，数据多，信息较分散，不利于系统分析结论，因此定义灰色关联度为:

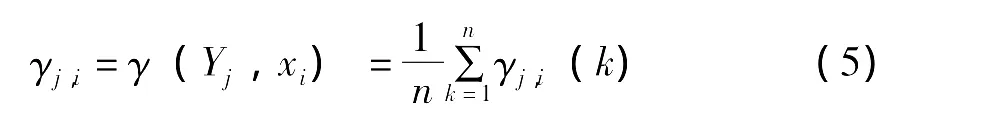
计算得到的xi与Y的灰色关联度越大，则表明xi对Y的影响程度越大。

根据公式 (3)-(5)可以分别计算得到成纱性能 (Y1，Y2，Y3，Y4)与纤维和半成品性能(x1，x2，…，x8)之间的灰色关联度，并依次选择关联度最大的5个 (为了与主成分分析方法进行比较，输入参数的数量相同)纤维性能指标作为神经网络的输入。用Matlab 7.1进行计算，计算结果如下:

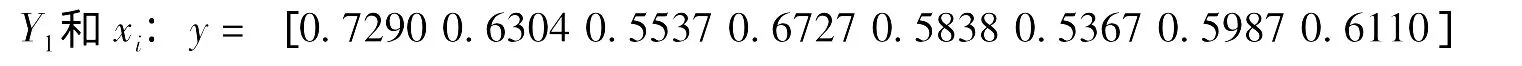
这表明，影响苎麻成纱强力的主要因素依次为:精干麻束纤维的平均断裂强度、精梳条麻粒、精干麻细度、精梳条回潮率、精梳条重量偏差。

这表明，影响苎麻成纱强力不匀的主要因素依次为:精干麻硬条率、精梳条重量不匀、精梳条并丝、精梳条重量偏差、精梳条回潮率。

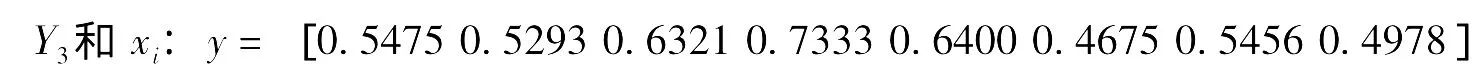
即，影响苎麻成纱条干的主要因素依次为:精梳条麻粒、精梳条并丝、精干麻硬条率、精梳条重量偏差、精干麻束纤维平均断裂强度。

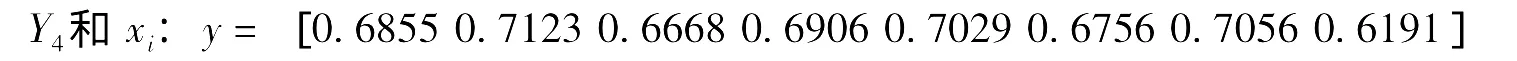
即，影响成纱麻粒的主要因素依次为:精干麻细度、精梳条重量偏差、精梳条并丝、精梳条麻粒、精干麻束纤维平均断裂强度。

通过灰色关联分析，选择了8个指标中最重要的5个指标作为神经网络的输入，从而使神经网络的输入节点数由8个减少到了5个。

4 BP神经网络

本文采用“反向传播”神经网络 (BP)进行建模。一般具有1个输入层、1个隐层、1个输出层的三层神经网络较为常用［6］。输入层节点的个数:当采用单纯的BP神经网络时，采用原有的8个变量作为输入，因此输入节点数为:8;经过主成分分析和灰关联分析后，输入节点数减少为5。输出层节点的个数:对Y1，Y2，Y3，Y4分别建立预测模型，因此输出层节点数为1。隐层的节点数根据公式 (6)进行计算［7］:

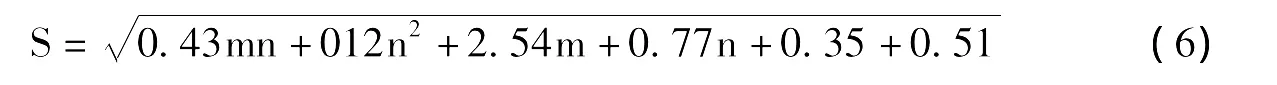
m-输出层的节点数;n-输入层的节点数。

因此，单纯的BP神经网络的结构为“8-5-1”，主成分分析和灰色关联分析神经网络的结构为 “5-4-1”。

BP神经网络的输入层和隐层之间的传递函数为:f(x)=2/(1+e)-2x-1;隐层和输出层之间的传递函数为:f(x)=x;训练次数:2000;训练精度:0.01;训练函数:traingdx，该函数是梯度下降法训练函数，学习速率是自适应的，预测结果较好。

5 预测结果与分析

本文分别采用三种方法对纯苎麻27.8tex(即36Nm)纱的强力等性能进行预测，并对三种方法的预测结果进行了比较。预测结果分别如表2-表5所示。

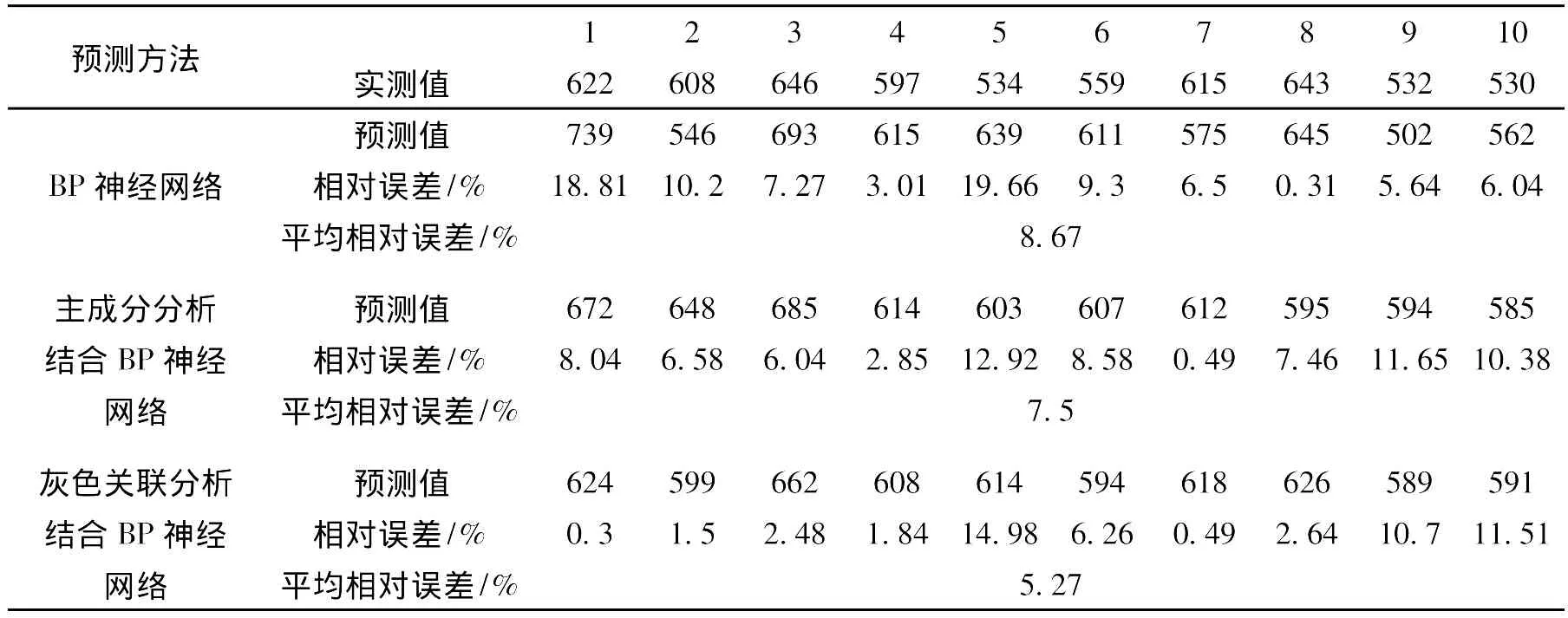
表2 成纱强力 (cN)预测结果Tab.2 Predicted results of yarn strength(cN)

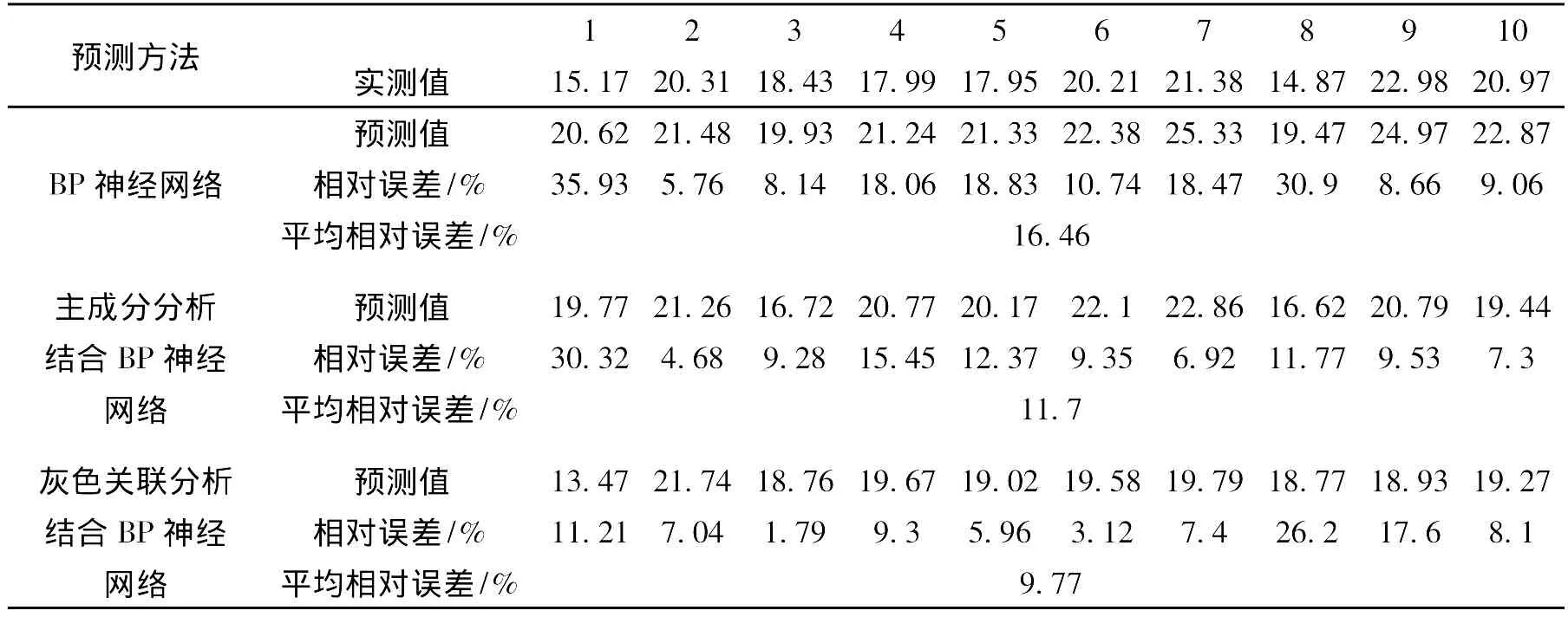
表3 成纱强不匀 (%)的预测结果Tab.3 Predicted results of yarn strength irregularity(%)

从表2-表5可得:主成分分析结合BP神经网络和灰色关联分析结合BP神经网络的预测结果均比单纯的BP神经网络好，其平均相对误差均减小至10%［8］以内，证明该预测模型是可以接受的，这是因为经过主成分分析和灰色关联分析后，神经网络输入层的节点数减少而且输入因子更具有代表性，从而简化了神经网络的结构使预测精度提高。对成纱强力、强不匀和条干进行预测时，灰色关联分析结合BP神经网络建立的预测模型的预测结果最准确，这可能是因为通过灰色关联分析选出的5个因素比主成分分析选出的5个主成分对成纱性能的影响程度更大。而对成纱麻粒进行预测时，主成分分析结合BP神经网络建立的模型的预测结果最准确，这可能是因为对成纱麻粒与纤维的性能指标进行灰色关联分析后，得到各个因素的灰关联度比较接近，这说明这些因素对成纱麻粒都有较大的影响，只选择前5个因素作为神经网络的输入可能导致信息的丢失而影响预测结果的准确性。

表4 成纱条干的预测结果Tab.4 Predicted results of yarn unevenness

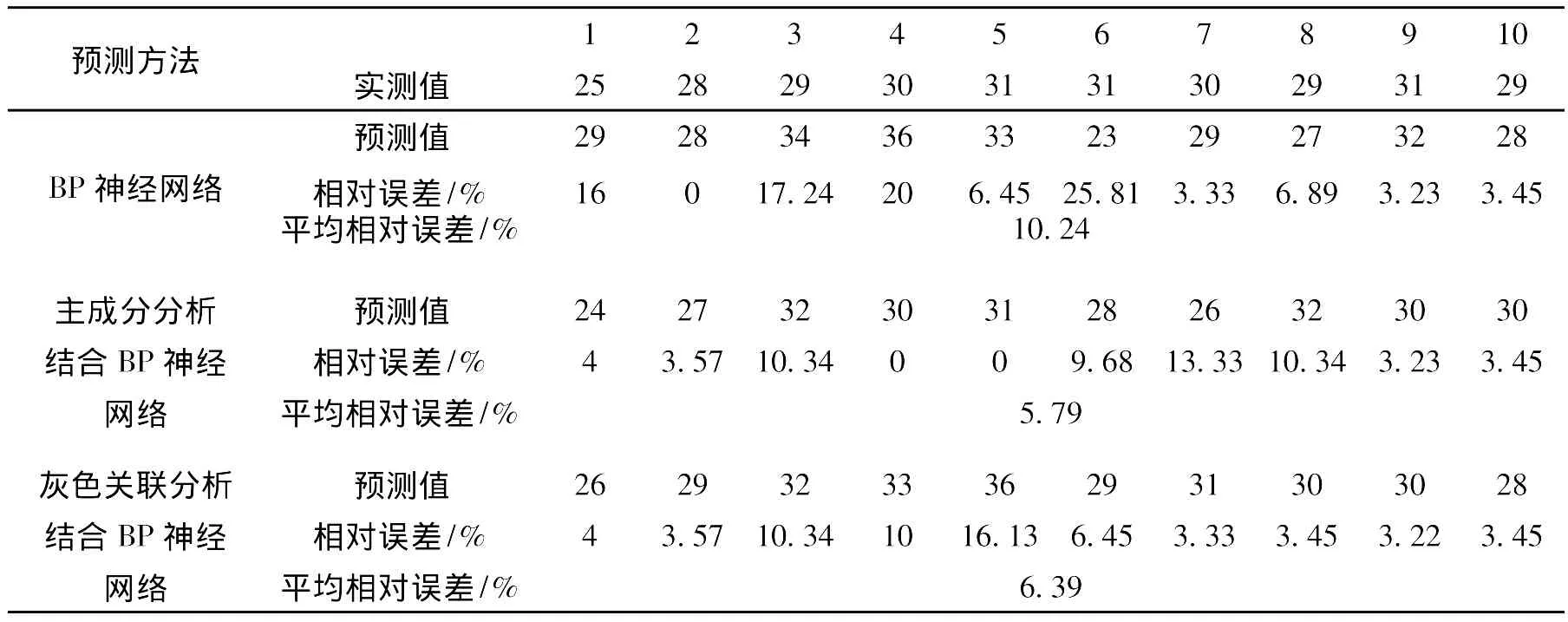
表5 成纱麻粒的预测结果Tab.5 Predicted results of yarn neps

6 结语

6.1 用主成分分析结合BP神经网络和灰色关联分析结合BP神经网络建立的预测模型比单纯的BP神经网络模型的预测结果好，平均相对误差小于或接近10%。

6.2 主成分分析是将原有的多个变量转换为几个不相关的综合指标;而灰色分析可以通过计算纤维性能与成纱性能之间的灰色关联度，分析得出纤维各个性能指标对成纱性能影响的重要程度，并结合实际生产得出成纱性能的各个影响因素之间的主次关系。

［1］ Zeguang Pei，Chongwen Yu.Prediction of the vortex yarn tenacity from some process and nozzle parameters based on numerical simulation and artificial neural network ［J］ .Textile Research Journal，2011，0(00):1-12.

［2］高惠璇.应用多元统计分析［M］.北京:北京大学出版社，2005.

［3］李晓峰.主麻纤维原料品质与成纱品质指标的灰关联分析［J］.纺织学报，2006，27(1):20-22.

［4］蔡煜东，姚林声.亚麻纤维品质与成纱质量的人工神经网络分析方法［J］.纺织基础科学学报，1993，6(4):307-309

［5］刘思峰，谢乃明.灰色系统理论及其应用［M］.北京:科学出版社，2008.

［6］ Guifen Yao，Jiansheng Guo，and Yongyuan Zhou.Predicting the warp breakage rate in weaving by neural network techniques［J］ .Textile Research Journal，2005，75(3):274-278.

［7］ Daqi Guo，Study on the linear primary function forword three layers neural network’s architecture with teachers，Journal of Computers，Vol.21，No.1，1998，pp.80-86.

［8］吕志军，智能挖掘与质量控制技术在纺织生产过程中的应用研究［D］.上海:东华大学，2007.