对两井定向平差计算方法及其准确度的探讨

彭伟平

(湖南水口山有色金属集团公司柏坊铜矿，湖南衡阳 421521)

1 “扭转法”和“边条件法”的不足及其解决方法

对于两井几何定向的内业计算，一般采用坐标轴扭转法[1](以下简称为“扭转法”)与边条件平差法[2](以下简称为“边条件法”)，“扭转法”不仅无法进行实测精度的评定(通常只作误差预计)，而且只适用于近似直伸形附合导线[3]，这是因为“扭转法”的平差计算模型[4]建立在测量系统误差基础之上，显然，这种平差模型是不合理的；图1所示扭转角的准确度Δθ不仅与井下导线测量精度有关，还与导线形状有关，相反，系统误差处理的方法与导线形状及量边偶然误差系数无关。虽然“边条件法”可以进行两井定向实测精度的评定，但边条件闭合差并不能全部反映测量误差对闭合差的影响[4]，如与两钢丝A、B连线成90°交角的导线边量边误差对边条件闭合差毫无影响，但对两井定向的精度影响很大[5]。由图1可知，“边条件法”仅消除了终点B′的纵向位移t，但没有消除终点B′的横向位移μ；由此可见，“扭转法”与“边条件法”的平差模型与测量误差的影响规律不一致，容易使导线产生扭转变形，使平差成果和精度评定的准确度大大降低。文献[6]的实例已经证明，附有虚拟观测值的条件平差法能够显著地提高无定向附合导线解算成果的准确度，为此，本文拟采用附有虚拟观测值(即虚拟右角)的条件平差法(以下简称为“虚拟权法”)，来消除井下连接导线测量误差对导线终点B′所产生的纵向闭合差与横向闭合差，从而确保两井定向平差成果与精度评定结果可靠。最后采用螺陀定向仪进行检测与验证。

2 “虚拟权法”的平差原理及其精度评定

2.1 “虚拟权法”的平差原理

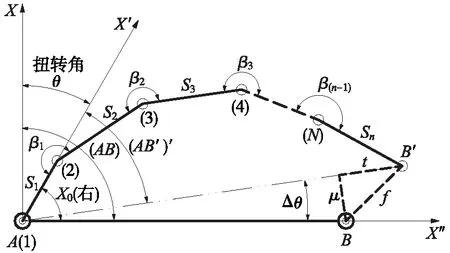
图1 井下无定向附合导线布设与误差分析

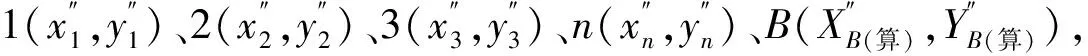
(2)

由条件方程(1)(2)组成法方程得

(4)

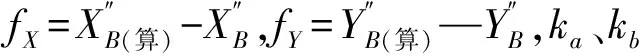
2.2 “虚拟权法”的精度评定

精度评定公式可由文献[7]列出，在此只列出定向边(3-4边)的权函数式为

F=-VX0(右)+Vβ1+Vβ2

(5)

2.3 虚拟观测值的确定

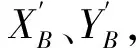
3 实例介绍

某矿联系测量采用通过两个立井的两井几何定向与陀螺定向的联合定向法(如图2所示)，图中实线为井上5 s级导线，单虚线为井下7 s级导线，双虚线为井下加测陀螺方位的定向边。井下导线量边偶然误差系数a=0.000 4，b=0.000 05，两井垂球线间距为54.6 m，井筒深为200 m，井筒垂球线投点的线量误差为e=±1 mm，近井点1到煤仓的方位角为272°37′50″，近井点1的坐标为XⅠ=9 208.973 m，YⅠ=8 439.580 m，井下定向边6—7使用JT15陀螺经纬仪加测陀螺方位角，其一次定向中误差为±17.1 s，定向边的陀螺方位角为55°46′00.4″，井上井下的观测数据见表1(数据来源于文献[8])。

3.1 平差计算

下面采用电脑EXCEL编程计算的方法，应用“扭转法”、“边条件法”及“虚拟权法”三种计算方法对井下连接导线分别进行计算，并将三种方法的计算结果与陀螺定向成果进行比较，三种方法的计算结果及比较结果见表2。

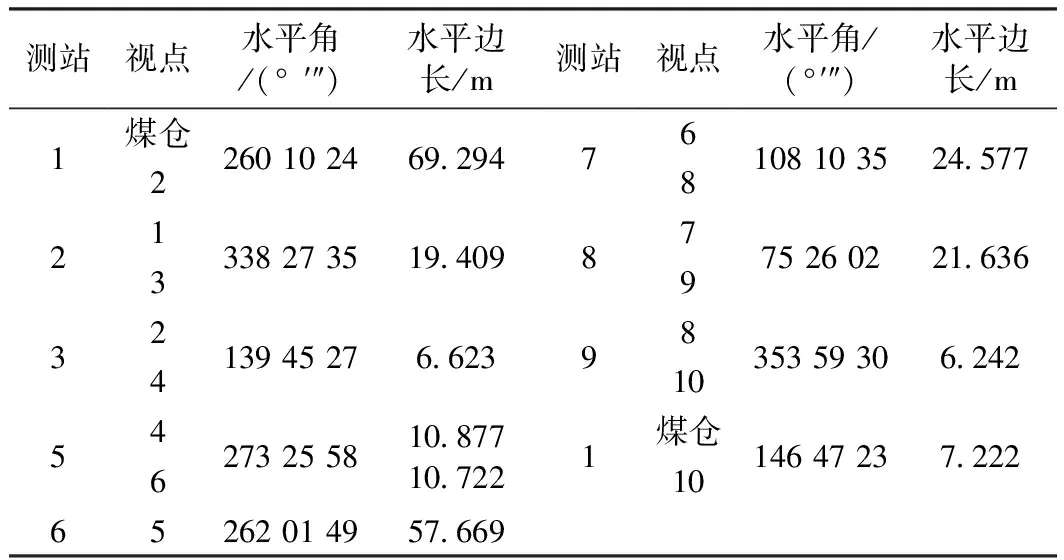
表1 两井定向时井上下观测数据

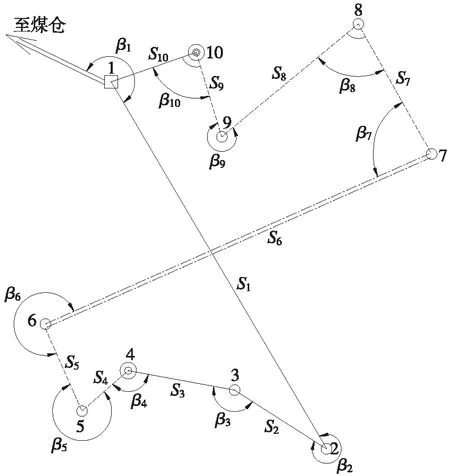
图2 两井定向的井上井下连接

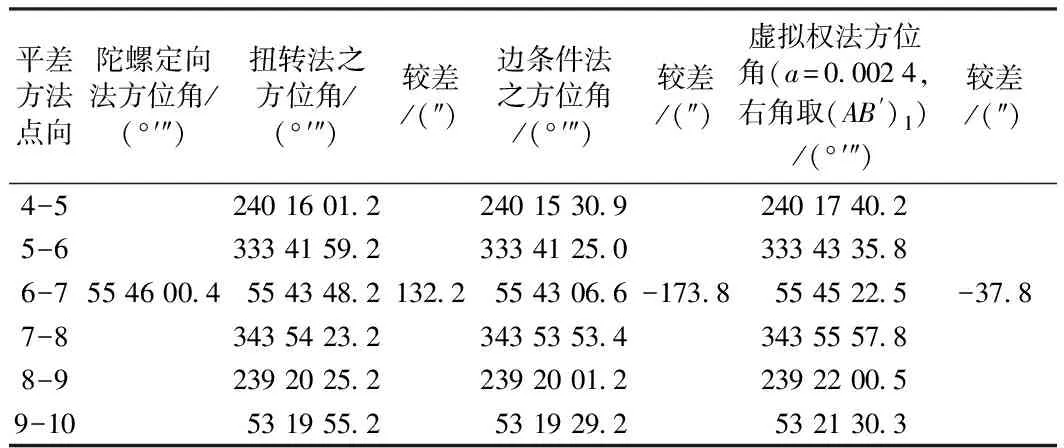
表2 平差结果与比较结果

3.2 精度评价

同一平差问题，同样的观测值与精度，同样的检验标准，实例证明(实例为曲折形导线，其直伸系数为K=0.42)，“扭转法”与“边条件法”的解算成果含有显著的系统偏差，但“虚拟权法”的解算成果只含有较小的偏差，这既充分证明了“虚拟权法”能显著地提高两井定向内业计算成果的准确度，又充分证明了“扭转法”与“边条件法”的平差方法存在不足。

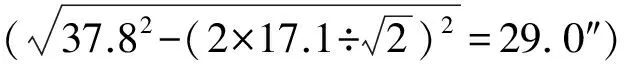
文献[8]的平差方法是错误的，因为该文未考虑地球曲率对地面边长AB的影响；因此，井上井下的A点(或B点)不在一个点上，钢丝处的连接角存在较大的粗差。

文献[2,10]认为，边条件平差法对提高地下导线精度很有必要，但本文的实例证明，边条件平差法反而降低了井下导线边方位角的准确度(这是因为“边条件法”没有消除终点B′的横向位移)；而且本人计算证明，量边偶然误差系数(大小)的变化对“边条件法”平差结果的影响很小，相反，量边偶然误差系数(大小)的变化对“虚拟权法”平差结果的影响很大。

应用附有参数的条件平差法时，其平差结果与“边条件法”的结果是相同的。因此，附有参数的条件平差法并不能提高两井定向解算成果的准确度。

4 结束语

误差理论分析表明，“边条件法”的平差模型与测量误差影响规律不一致。实践证明，当井下曲折形导线量边误差的影响较大时，特别是当有可靠性差的导线边存在(或钢丝横向摆动)或井下导线的量边质量较低(即导线的坐标相对闭合差在1/10 000左右)时，“扭转法”与“边条件法”的解算成果含有显著的系统偏差，而“虚拟权法”的解算成果只含有较小的系统偏差。

“虚拟权法”全面考虑了导线测量误差对导线终点纵向与横向的影响，并且按照测量偶然误差的影响规律进行平差。因此，只要采用实际闭合差来确定量边偶然误差系数和边长的权，就能够合理消除井下连接导线测量误差所产生的的纵、横向闭合差，就能确保两井定向平差成果与实测精度评定的可靠性。

“扭转法”的两井定向误差预计值与其实际偏差相差很大，但“虚拟权法”的精度评定结果(即实测精度)与其实际偏差基本一致。

最后必须指出的是，在现有井下定向工程测量实践中，通常使用“扭转法”与“边条件法”进行两井定向的平差计算，“扭转法”与“边条件法”平差理论的缺陷所产生的工程质量问题并没有凸显出来，这是因为井下量边精度较高(导线的坐标相对闭合差一般小于1/20 000)，量边误差对两井定向精度的影响控制在较小范围内的缘故。

参考文献

[1] 张国良.矿山测量学[M].徐州：中国矿业大学出版社，2001

[2] 李青岳.工程测量学[M].北京：测绘出版社，1984：242-243

[3] 彭伟平.附合导线近似平差的新方法[J].测绘科技通讯，1994(3)：34-37

[4] 牛长旭.矿山测量[M].北京：冶金工业出版社，1983

[5] 冯仲科，陈于恒.两井几何定向系统的可靠性分析[J].矿山测量，1993(1)：24-27

[6] 彭伟平.无定向附合导线平差的新方法[J].有色金属：矿山部分，2002(5)：42-45

[7] 武汉测绘科技大学测量平差教研室.测量平差基础(第三版 )[M].北京：测绘出版社，1996

[8] 邓军，王胜利.加测陀螺定向边的井下导线平差方法探讨[J].资源环境与工程，2006(2)：163-167

[9] 刘延伯.工程测量[M].北京：冶金工业出版社，1984：229-233

[10] 徐茂林.利用一井定向资料完成两井定向的方法[J].测绘通报，2002(1)：29-31