基于强度折减理论的西南某库岸滑坡稳定性FLAC3D分析

李勤光

(中铁工程设计咨询集团有限公司,北京 100055)

滑坡灾害是一种常见的地质灾害,具有不可避免性的特点,但采用防灾减灾措施,可以最大限度地降低灾害损失。制定防灾减灾措施前,需首先对滑坡的稳定性进行相关分析。关于滑坡稳定性分析方法,自弗伦纽斯提出圆弧滑动法以来,已经出现了包括极限平衡法、数值模拟方法等多种方法。随着计算机技术的发展,采用包括有限元法、有限差分法在内的数值模拟方法分析边坡稳定性已被广泛应用。

西南某库岸滑坡位于我国西南某省一新县城建设规划区,滑坡体上将进行新县城的部分建设工作。根据现场地质资料、库岸滑坡影响因素调查,基于强度折减理论,运用FLAC3D数值分析工具,对自然状态和蓄水状态下的滑坡稳定性进行综合稳定性分析。

1 滑坡区工程地质条件

该滑坡体地形上总体西高东低,地面高程840～1 115 m,最大相对高差375 m,属中、低山斜坡地貌。场区大渡河侧坡度较陡,平均坡度为40°～50°,最陡段坡度达到60°,流沙河侧坡度相对平缓,坡度一般为10°～25°。场地区冲沟较发育,冲沟规模多较小。

地层主要有第四系全新统人工堆积层(Q4ml)、全新统残坡积层(Q4el+dl)、全新统滑坡堆积层(Q4del)等松散层,奥陶系下统红石崖组(O3h)基岩地层。基岩为大致北东倾向的单斜岩层。滑坡堆积层主要由第四系全新统滑坡堆积层(Q4del)构成,成分主要为耕植土、粉质黏土、块石土、角砾土等组成。

研究区的地下水与地表水均贫乏。地表水来源主要靠大气降水补给,区内冲沟较发育,平时多为干沟,仅雨季有季节性水流。冲沟上段多叉枝状,下段切割较深而窄,沟床多基岩裸露。

2 基于强度折减的FALC3D稳定性分析

2.1 计算模型

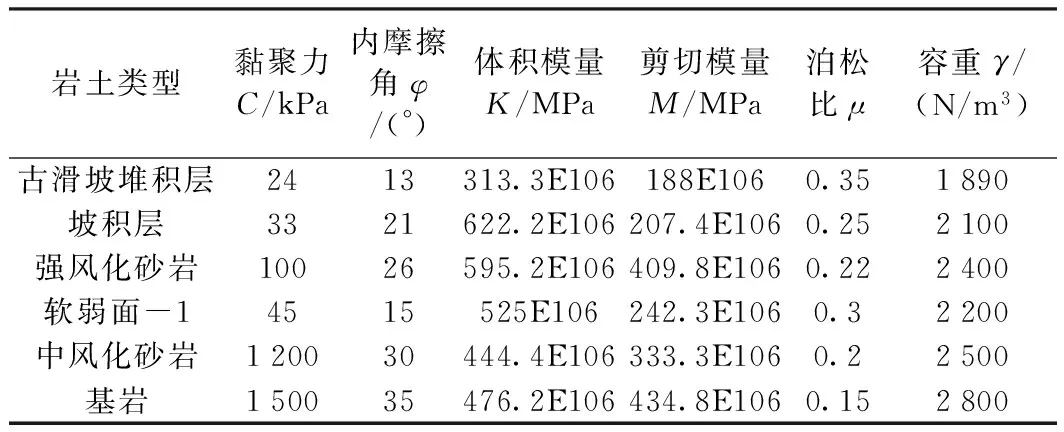
本文基于图1所示的三个地质模型建立三维的数值计算模型(如图2)。模型边界条件为左、右边界水平方向约束,底部边界固定约束,上部为自由边界。计算时,仅考虑自重应力作用,暂不考虑构造应力的影响。两个水平方向尺寸分别为800 m、1 000 m。模型共有14 127个节点,12 336个单元。模型中各物理力学参数根据勘察报告、工程地质类比及参考相关规范手册最终确定,如表1所示。

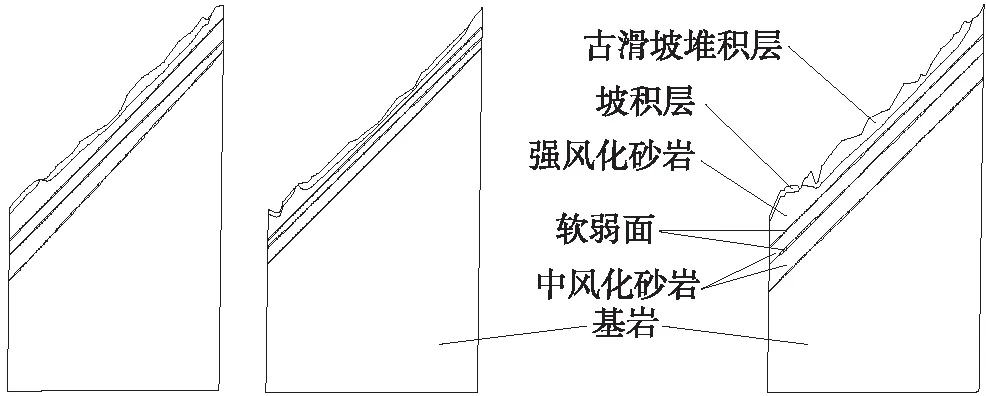
图1 场区地质模型

图2 FLAC3D数值计算模型

岩土类型黏聚力C/kPa内摩擦角φ/(°)体积模量K/MPa剪切模量M/MPa泊松比μ容重γ/(N/m3)古滑坡堆积层2413313.3E106188E1060.351890坡积层3321622.2E106207.4E1060.252100强风化砂岩10026595.2E106409.8E1060.222400软弱面-14515525E106242.3E1060.32200中风化砂岩120030444.4E106333.3E1060.22500基岩150035476.2E106434.8E1060.152800

2.2 计算条件

由于天然力、人类活动及工程开挖等,现场出现许多高大的陡坎。这些陡坎在进行整体边坡稳定性强度折减运算时,很容易就出现不收敛及局部剪应变增量的贯通,造成计算中断,从而影响整个边坡稳定性计算的继续。为此,本文分两步计算边坡的稳定性,首先：进行FLAC3D强度折减运算,计算边坡在陡坎影响下的局部安全系数；然后再对陡坎进行治理基础上进行第二步FLAC3D强度折减运算,计算边坡整体的稳定性。

(1)局部稳定性

计算过程从折减系数为1.00(即F=1.00)开始,然后以每步长为ΔF=0.01递增,直至边坡局部发生破坏为止(图3～图10)。从图3～图10可以看出,坡体剪应变增量(SSI)随着折减系数的增加而逐渐增大,而剪应变增量较大的地方,最易变形破坏,最可能成为潜在的滑动面；相反,剪应变增量较小或者是基本上没有什么变化的部位,一般不易变形破坏,也不可能成为潜在的滑动面；且当折减系数为1.08时,计算不再收敛,说明当折减系数为1.07时,边坡局部(陡坎处)剪应变增量达到最大,此时,边坡局部沿陡坎发生变形破坏。

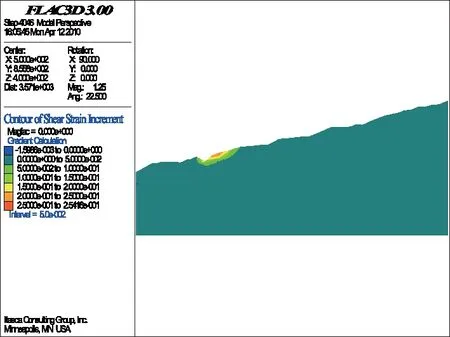
图3 折减系数为1.00时的SSI

图4 折减系数为1.01时的SSI

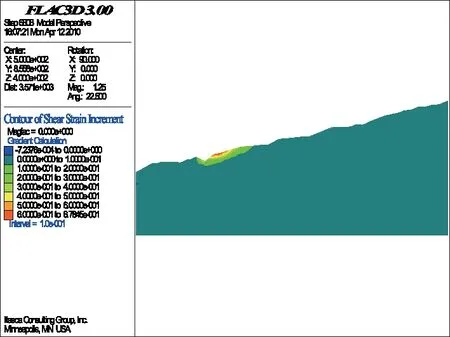
图5 折减系数为1.02时的SSI

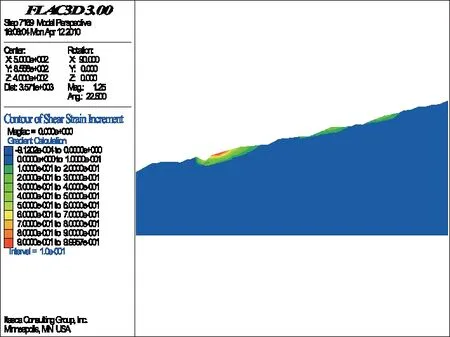
图6 折减系数为1.03时的SSI

图7 折减系数为1.04时的SSI

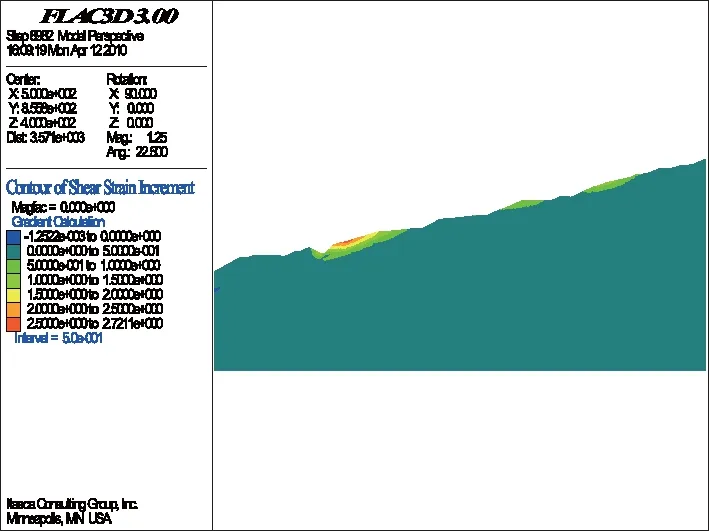
图8 折减系数为1.05时的SSI

图9 折减系数为1.06时的SSI

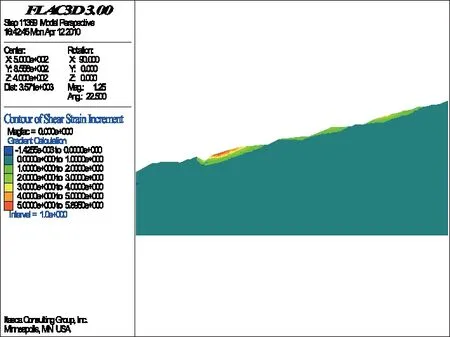
图10 折减系数为1.07时的SSI

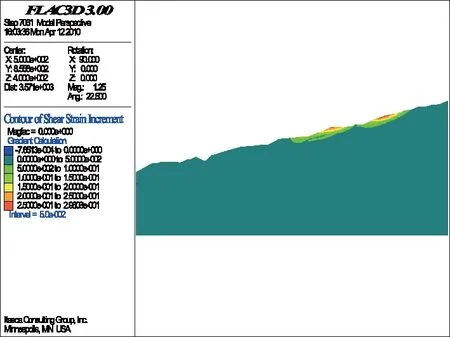
图11 折减系数为1.00时的SSI

(2)整体稳定性

对边坡局部的陡坎采取一定的措施后,计算整个边坡的稳定性。同样,折减计算过程从折减系数为1.0(即F=1.0)开始(如图11),然后以每步长为ΔF=0.1递增,直至计算不再收敛,然后降低步长ΔF=0.01递增,直至边坡剪应变增量贯通,边坡整体发生变形破坏为止。从计算结果来看,折减系数在1.0、1.1、1.2、1.3、1.35时,剪应变增量逐渐增大,但尚未从坡顶到坡脚贯通,虽然边坡体内部已有部分出现剪切破坏的迹象,但由于剪应变增量没有整体贯通,所以边坡整体还是处于稳定状态。但当折减系数为1.36时(如图12),在边坡上部剪切破坏的基础上,滑动面进一步贯通,此时,滑动面已贯穿边坡上部土体内,边坡将沿该滑动面发生变形破坏。数值模拟计算在折减系数为1.4时不再收敛,为此降低折减系数步长ΔF,计算最终收敛于F=1.36。

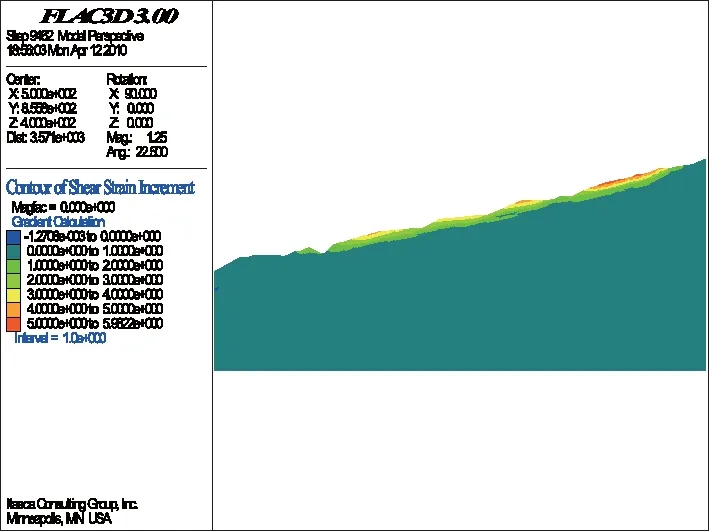
图12 折减系数为1.36时的SSI

2.3 蓄水状态下的稳定性计算

水库正常蓄水后,由于水的物理、化学作用,将会使岸坡的荷载和岸坡的材料性质发生变化,而这些变化很可能导致岸坡失稳以及古滑坡复活,从而会对县城建设、通航、水库库容等产生严重影响。因此,本文对正常蓄水条件下边坡稳定性进行了计算分析。

该边坡地面高程在840～1 115 m之间,而正常蓄水位为850 m。可见,坡脚部分将浸没在正常水位以下。模拟时，850 m水位面以上边坡的容重采用天然状态下的容重,水位面以下部分的容重取有效容重,以此来进行水库蓄水状态下边坡的稳定性模拟和计算。

计算结果表明,当折减系数为1.04时,计算不再收敛,坡脚剪应变增量出现局部贯通现象,边坡安全系数降为1.04,说明随着库水位升至850 m,坡脚的稳定性显著降低(如图13、图14所示)。

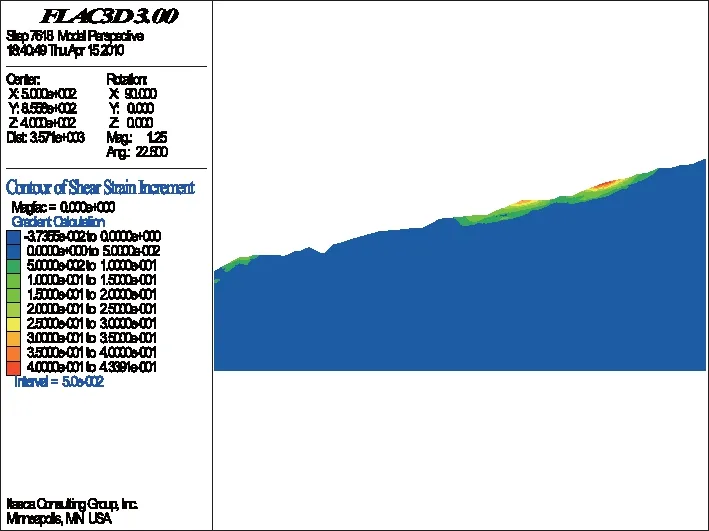
图13 折减系数为1.00时的SSI

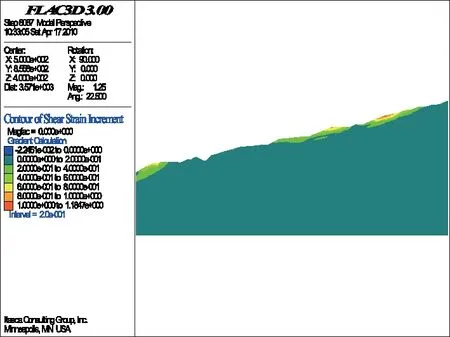
图14 折减系数为1.04时的SSI

3 结论

本文所研究边坡不仅关系到水库的安全运营,还牵涉到当地新县城的稳定发展,边坡破坏后将会给社会、经济和环境带来重大影响。因此,根据相关规范《水利水电工程边坡设计规范》，《滑坡防治工程勘查规范》,其边坡级别应属1级边坡,也即水库蓄水正常运营状况下,其边坡安全系数应达到1.25以上。

计算表明：天然状况下,边坡局部陡坎、陡壁处可能出现变形及破坏的情况,局部处于基本稳定状态；而边坡的整体稳定性还是比较好的,传递系数法安全系数为1.336,FLAC3D强度折减法安全系数为1.36,满足规范要求,整体处于稳定状态。

当库水位蓄至850 m高度时,边坡的安全系数降低至1.04,边坡欠稳定,坡脚在库水的浸泡、侵蚀等作用下很容易变形破坏,一旦坡脚破坏,在滑坡前缘的拉动下,很可能造成滑坡整体的不稳。因此,为保证水库的正常运营及新县城的安全，必须对该边坡进行切实有效的防治。

参考文献

[1] Fredlund, D.G. & Krahn, J. Comparison of slope stability methods of analysis. Canadian Geotechnical Journal， 1977，14(3):429-439

[2] 陈祖煜.土质边坡稳定分析——原理、方法、程序[M].北京：中国水利水电出版社，2003

[3] 赵尚毅,郑颖人,邓卫东.用有限元强度折减法进行节理岩质边坡稳定性分析[J].岩土力学与工程学报，2003，22(2):254-260

[4] 陈祖煜.土质滑坡稳定分析——原理方法程序[M].北京:中国水利水电出版社，2003

[5] 李新平,郭运华,彭元平,等.基于FLAC3D的改进边坡极限状态确定方法[J].岩石力学与工程学报,2005,24(增2):5287-5291

[6] 陈新泽,唐辉明,杨有成,等.基于FLAC3D强度折减法滑坡三维稳定性研究——以三峡库区白果树古滑坡群为例[J].水文地质与工程地质，2008(2):24-29

[7] 刘建国.水下边坡稳定性计算模式的探讨[J].上海铁道大学学报，2000，21(2):35-38