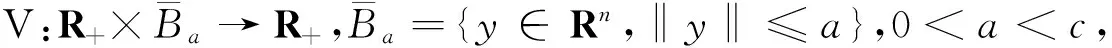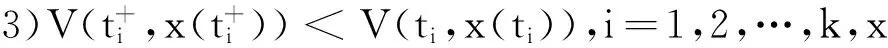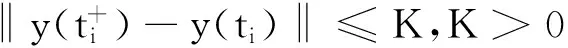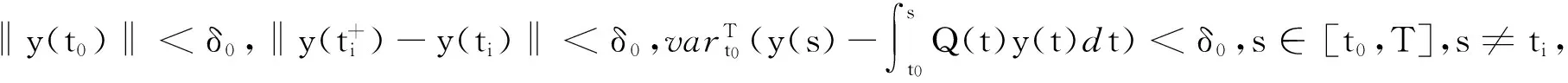一类线性脉冲微分系统的变差稳定性
2012-05-15李宝麟王倩倩
李宝麟, 王倩倩
(西北师范大学 数学与信息科学学院 甘肃 兰州 730070)
0 引言
考虑一类线性脉冲微分系统:
(1)


3)Bi∈L(Rn),ai∈Rn,i=1,2,…,k且I+Bi可逆,I为n阶单位矩阵.
作者在文献[1]工作的基础上讨论了线性脉冲微分系统有界变差解的稳定性,建立了变差稳定性和渐近变差稳定性的Lyapunov型定理.这是对文献[2]中一类不连续系统有界变差解的变差稳定性结果的本质推广.
由于稳定性不是系统单个解的性质,而是其所有解的共同性质,向量值函数P(t)并不影响这个性质[3],因此系统(1)的变差稳定性等价于系统
(2)
的变差稳定性.
1 预备知识
设[a,b]为实有限区间,Rn为实n维欧式空间.x:[a,b]→Rn为[a,b]上的向量值函数.对x∈Rn,‖x‖为Rn上的欧式范数.
定义1[1-2,4]函数x(t)在[a,b]上是Henstock可积的,如果存在A∈Rn,对任意的ε>0,存在正值函数δ(t):[a,b]→(0,+),使得对[a,b]的任何δ-精细分划D:a=τ0<τ1<…<τk=b及{ξ1,ξ2,…,ξk}满足ξi-δ(ξi)<τi-1≤ξi≤τi<ξi+δ(ξi),i=1,2,…,k,有记x(t)在[a,b]上的Henstock积分为x(t)dt=A.
设c>0,令Bc={x∈Rn,‖x‖ 定义2[1]设函数f:G→Rn为 Caratheodory函数,f∈V(G,h,ω),如果f(t,x)满足下列条件: 1)存在正值函数δ:(ti,ti+1]→R+,(ti,ti+1]⊂[t0,T]⊂(a,b),i=0,1,…,k-1,对每个区间[u,v]满足τ∈[u,v]⊂(τ-δ(τ),τ+δ(τ))⊂(ti,ti+1]及x∈Bc有‖f(τ,x)(v-u)‖≤h(v)-h(u); 2)对每个区间[u,v]满足τ∈[u,v]⊂(τ-δ(τ),τ+δ(τ))⊂(ti,ti+1],以及所有的x,y∈Bc有‖f(τ,x)-f(τ,y)‖(v-u)≤ω(‖x-y‖)(h(v)-h(u)); 3)对每个定义在(ti,ti+1]⊂[t0,T]⊂(a,b)上的阶梯函数ψ(t),f(t,ψ(t))在(ti,ti+1],i=0,1,…,k-1上是Henstock可积的. 其中,h:[t0,T]→R是定义在[t0,T]上的单调增加左连续函数,而ω:[0,+)→R是连续增函数,且ω(r)>0(r>0),ω(0)=0. 对x∈Rn,t∈R+,令f(t,x)=Q(t)x,若(t0,x0)∈(a,b)×Bc给定,对任意的[u,v]⊂[t0,T]⊂(a,b),x∈Bc,t∈[u,v],t≠ti,i=1,2,…,k,有 ‖f(t,x)(v-u)‖ =‖Q(t)x(v-u)‖ =h(v)-h(u), 对任意的[u,v]⊂[t0,T],x,y∈Bc,t∈[u,v],t≠ti,i=1,2,…,k,有 ‖f(t,x)-f(t,y)‖(v-u) =‖Q(t)x-Q(t)y‖(v-u) =ω(‖x-y‖)(h(v)-h(u)), 这里ω:[0,+)→R,ω(r)=r,r>0. 对定义在(ti,ti+1]上的阶梯函数ψ(t),则ψ(t)必为有界变差函数,因此f(t,ψ(t))=Q(t)ψ(t)在(ti,ti+1],i=0,1,…,k-1上是Henstock可积的,则可知f(t,x)∈V(G,h,ω). 对任意的t∈[t0,T],t≠ti,i=1,2,…,k,有f(t,0)=0,称函数x(t)=0是系统(2)在[t0,T]上的零解. 引理3[1]设f(t,x)∈V(G,h,ω),且(t0,x0)∈G,则一定存在δ>0使得系统(2)在区间[t0,t0+δ]上存在满足x(t0)=x0的有界变差解x(t). 定义5若系统(2)的零解既是变差稳定的,又是变差吸引的,则称系统(2)的零解是渐近变差稳定的. 引理5[2,5]设[a,b]⊂R+,f,g:[a,b]→R是在(a,b]上的左连续函数,如果对任意的σ∈[a,b],存在δ(σ),使得对任意η∈(0,δ(σ)),有不等式f(σ+η)-f(σ)≤g(σ+η)-g(σ)成立,则对任意s∈[a,b]有f(s)-f(a)≤g(s)-g(a). 引理6设有函数V:R+×Rn→R,对任意x∈Rn,V(·,x):R+→R在(0,+)左连续.进一步,设以下条件成立: 1)对任意x,y∈Rn,常数L>0,有 |V(t,x)-V(t,y)|≤L‖x-y‖; 2)对系统(2)在[t0,T]⊂[a,b]上的每个解x(t),当(t,x)∈R+×Rn,t=ti,i=1,2,…,k时,有 3)存在实函数Φ:Rn→R,使得对系统(2)在[t0,T]上的每个解x(t),(t,x)∈R+×Rn,t≠ti,i=1,2,…,k,有 当(t,x)∈R+×Rn,t≠ti时,有 (3) 当(t,x)∈R+×Rn,t=ti时,有 (4) V(t,x)≥b(‖x‖), (5) V(t,0)=0; (6) ‖V(t,x)-V(t,y)‖≤L‖x-y‖; (7) 证明由于对系统 (2)的每个解x(t),t∈[t0,T],t≠ti,i=1,2,…,k,函数V(t,x)是不增函数,所以有 (8) 又由(4)、(6)、(7)式,对任意的t∈[t0,T],t=ti,有 (9) V(t,y(t))<2Lδ(ε)<3Lδ(ε)<α(ε),t∈[t0,T],t≠ti; (10) 由(9)式,有 (11) 与(10)、(11)式矛盾.因此对所有的t∈[t0,T],有‖y(t)‖<ε,由定义 3 可知系统(2)的零解是变差稳定的. 证明由已知条件可得,函数V(t,x(t))对系统(2)的每个解x(t)是不增的,又由定理 1可知,系统(2)的零解是变差稳定的.因此根据定义5,只需证明系统(2)的零解是变差吸引的. (12) ≤L‖y(t0)‖-Lδ0 <3Lδ0+W(s′-t0) <3Lδ0. 参考文献: [1] 李宝麟,吴卫红.一类固定时刻脉冲微分系统的有界变差解[J]. 西北师范大学学报:自然科学版,2009,45(4):1-5. [2] 李宝麟,尚德泉. 一类不连续系统的变差稳定性[J]. 西北师范大学学报:自然科学版,2006,42(2):15-18. [3] Ashordia M, Kekelia N. On effective sufficient conditions for stability of linear systems of impulsive equations[J]. Mem Differential Equations Math Phys,2003,28:147-151. [4] 吴从析,李宝麟. 不连续系统的有界变差解[J]. 数学研究,1998,31(4):417-427. [5] Schwabik S. Generalized Ordinary Differential Equations[M]. Singapore:World Scientific,1992:329-348.



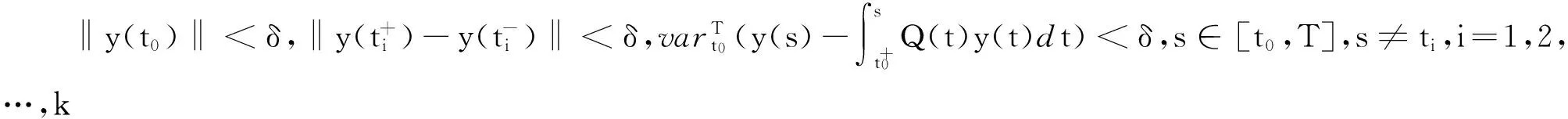

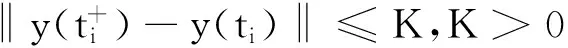

2 主要结果