基于粒子群文化算法的变电站选址与定容

杨明海，刘 洪，王成山，葛少云，曾 涛

(1. 天津大学智能电网教育部重点实验室，天津 300072；2. 成都电业局金堂供电局，成都 610400)

随着国民经济的快速发展，全社会对电力的需求量也不断增长．但是，受长期以来“重发轻供不管用”建设思想的惯性影响，我国一些地区配电网存在着电源结构矛盾突出的问题，从而影响了供电可靠性和安全性，并进一步制约了当地社会与经济的发展．

城市电网是电力系统的重要组成部分，也是电力系统的主要负荷中心，同时又是城市现代化建设的重要基础设施之一[1]．科学的城市电网规划，可以保证电网改造的合理性和电网运行的安全性与经济性，因此成为当前电力部门的一项重要任务．并且，由于城市电网规划还是一项规模庞大、不确定因素多且涉及领域广的工作[2]，因此与其相关的研究与实践工作面临着很多困难和挑战．

变电站选址与定容在整个规划过程中起着承上启下的重要作用，并且该规划方案的优劣将直接影响后续的高、中压网络规划项目以及电网的供电可靠性与经济性．另一方面，变电站选址与定容实际上是复杂的大规模、非线性的混合整数优化问题．目前已经有众多学者开展了一些研究工作，按照是否预先具有待选站址可分为2类.

第 1类方法是根据规划人员的经验提出变电站的备选位置，进而利用优化算法进行寻优[3-4]．这类算法的优点是，由于待选站址已经结合了很多实际情况，因此最终结果均具有较好的适应性．而缺点是需要事先进行很多实际的筛选工作，工作量大，对已有经验依赖性强．

第 2类方法是利用算法的大范围搜索所进行的完全自动选址方法[5-6]．这种算法的优点是前期工作量小；缺点是所选的站址结果很可能并不适宜，例如坐落于湖泊、街道、繁华地段等，需要人为调整，但是某些站址的局部调整将导致与周围变电站的负荷、供电范围的重新划分，进而影响整体方案的经济性．与此同时，这类算法也普遍存在收敛速度慢，不能很好找到全局最优解的缺点．

为此，笔者充分结合粒子群算法收敛快速、寻优范围大以及文化算法进化性好等优势，构建了可用于变电站规划的粒子群文化算法．与此同时，还在初始站址选择、变电站供电范围划分等方面做了一系列改进，从而使得本算法的寻优速度与寻优质量方面进一步提高．

1 变电站选址与定容的数学模型

基于投资费用时间价值的充分考虑，所提出变电站优化规划数学模型的目标函数以最小年费用值为选取原则，包含以下 3个方面：①变电站投资与运行年费用；②中压线路综合投资年费用；③中压线路网损年费用．

最终确定的变电站最小年费用模型表示为

式中：Station为折算到每年的变电站年投资与运行费用；Feeder为折算到每年的中压馈线投资费用；Lost为估算的中压线路年网损费用；N为已有和新建变电站的总数；Si为第i个变电站的容量；e(Si)为第i个变电站的负载率；Ji为第 i个变电站所供负荷的集合；J为全体负荷点的集合；lij为变电站 i与负荷点 j之间线路的长度；Wj为第 j点的负荷(有功负荷)；cos φ为功率因数；Ri为第 i个变电站供电半径的限制．3种费用的表达式分别为

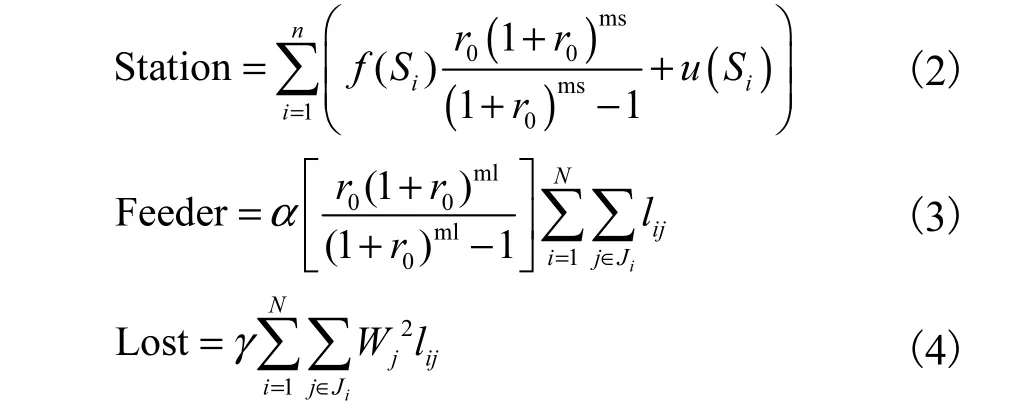
式中：f(Si)为第 i个新建变电站的投资费用；u(Si)为第 i个新建变电站的年运行费用；n为新建变电站的个数；ms为变电站的折旧年限；ml为变电站低压侧线路折旧年限；r0为贴现率；α为单位长度线路投资费用；γ为线路网损折算系数．

在传统模型中，变电站到负荷点的供电距离基本上采用的是 2点间的直线距离，但由于街道地形、接线模式等方面的影响，线路的实际长度往往大于该直线距离．本文中采用站网分解的优化方法来考虑变电站出线长度．若变电站与负荷点的坐标分别为(xi，yi)和(xj，yj)，则线路长度 lij计算式为

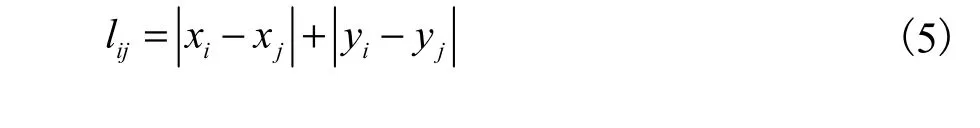
2 粒子群文化算法

2.1 粒子群算法

PSO算法源于对鸟群捕食的研究，当一群鸟在随机搜寻食物的时候，若此区域只有一块食物，则找到食物的最简单有效的策略即搜寻当前距食物最近的鸟的周边区域．PSO算法就是基于这个启示而产生的，并最终用于解决优化问题[7-8]．

对应于上述场景，优化问题的解相当于搜索空间中某只鸟的位置，算法中称这些鸟为“粒子”．每个粒子都有自己的用于决定飞行的方向和距离的位置和速度，此外还有一个由被优化函数所决定的适应值．在每一次迭代中，粒子一般追踪 2个“极值”：一个极值是粒子本身所找到的最优解，即个体极值点(用pbest表示其位置)；全局版PSO中的另一个极值则是全部粒子目前所找到的最优解，即全局极值点(用gbest表示其位置)，而局部版PSO的另一个极值则是其中一部分粒子的最优解，即局部极值点(用lbest表示其位置)．基于这2个极值点，对于D维空间中位置为 xi=(xi1,xi2,… ,xiD)Τ、速 度 为 vi=(vi1,vi2,… ,viD)Τ的粒子i，速度和位置更新方程为

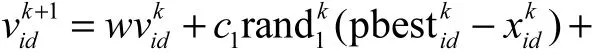
2.2 文化算法

“文化”被定义为“在社会中的不同人群之间和不同年代的人群之间历史地传递的、用符号表示的概念现象的系统[11]”．学者Renfrew[12]指出随着时间的迁移，人类在进化过程中逐渐掌握提取、掌握和传播信息知识的能力，这正是人类区别其他物种的特有能力．受此启发，文化系统的演化模型[13-14]由Reynolds[15]于1994年提出．

文化算法是模拟文化演化过程的计算模型，主要由上下 2层空间框架组成的．下层为主群体空间，上层为信仰空间．其中，主群体空间是算法求解的主空间，通过“进化”操作和“结果评价”进行自迭代求解，从而不断产生知识，然后通过“接受”操作来保存到信仰空间，信仰空间通过“自进化”操作进行更新，并通过“影响”操作对主群体空间的指导进一步进化．这就是主群体空间与信仰空间进行信息交流的“双演化双促进”机制．

2.3 粒子群文化算法框架

通过上述分析可知：文化算法的进化机制更适用于寻优过程的整体管理，容易得到更优化的结果，但该算法在寻优速度方面有所欠缺；粒子群算法则在寻优速度方面具有较大的优势，并且更适于微观寻优．因此，将粒子群算法作为文化算法的底层寻优算法，从而形成粒子群文化算法[16]．

粒子群文化算法主要由2部分组成：①基于粒子群的主群体空间；②利用知识源约束的信仰空间．2个空间均具有各自群体并行演化的能力，下层主群体空间为上层信仰空间贡献精英个体，上层信仰空间经知识演化后为下层主群体空间贡献精英个体．这样的“双演化双促进”能增加粒子群的群体多样性，避免“早熟”，进而提高计算精度和效率．粒子群文化算法模型框架如图1所示．

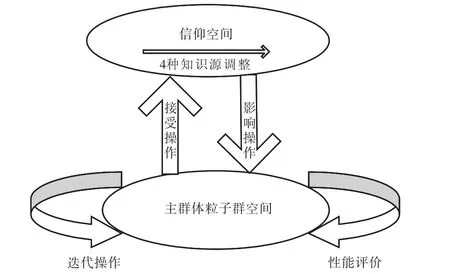
图1 粒子群文化算法框架结构Fig.1 Framework of cultural algorithm of particle swarm

3 基于粒子群文化算法的变电站规划

3.1 算法流程

笔者所提出用于变电站优化规划的粒子群文化算法流程如图2所示．

3.2 新建变电站个数的确定

根据《城市电网规划设计导则》，各级电网的容载比值 w＝pcap/pload，容载比的上、下限分别为 wmax和 wmin．若区域已有变电容量为 pcap，预测总负荷为pnew-load，则区域需增容量上限 pcap-max和下限 pcap-min分别为

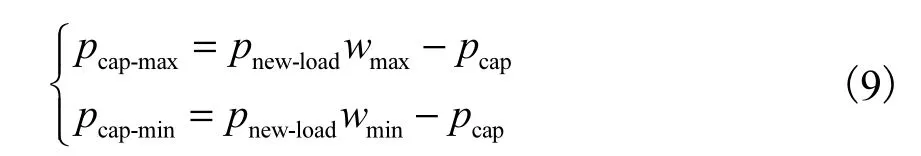
若单台变压器容量为 pi以及新建站的变压器台数为 N(2或 3)，则可以确定单个新建站的组合容量值 pcap1＝piN，进而计算新建站数上下限 Nmax和 Nmin分别为

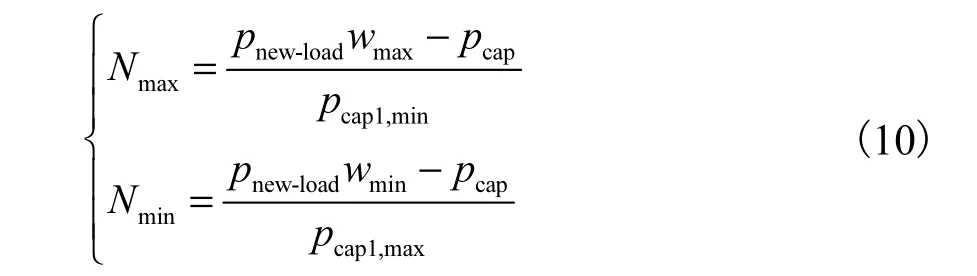
式中 pcap1,max和 pcap1,min分别为新建站的可选最大和最小容量．

图2 粒子群文化算法流程Fig.2 Flow chart of cultural algorithm of particle swarm

3.3 新建变电站容量配置

基于所确定的新建站数m，并根据新建站候选容量类型，以年费用最小为目标、以满足变电站容载比要求为约束来建立数学模型，最终确定几组较优的新建站容量组合．具体数学模型为

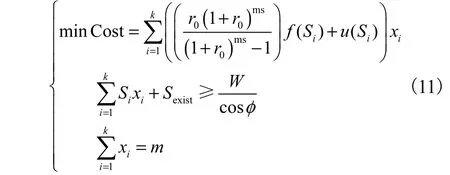
式中：k为变电站候选类型的个数；xi为第i种候选类型变电站的建设个数；Sexit为已有站容量(已考虑负载率)；W为总负荷．

式(11)中未知量xi是整数型的，且候选变电站类型有限，因此新建站容量组合确定的求解规模比较小．本文将其视为“0～1”整数规划问题，并采用隐枚举法来解决这一问题．

3.4 初始粒子群的形成

(1) 对每一个负荷点搜索以其为中心、以 d1为半径的范围，并对范围内的负荷进行求和，即

式中：l为负荷点的总数；pLoad,i为每一个负荷点的负荷；pTotal,j为以负荷点j为中心、以d1为半径的范围内的负荷总和；d1由相应电压等级所对应供电半径来确定．

(2) 对 pTotal,j进行由大到小的排序，从而形成新的点负荷数组 pL[j]，然后将第 1个负荷点的坐标加上较小的随机数得到第1个新建站的初始坐标为式中：pid_i[i].x是第 i个粒子中第 1个新建站的 x轴坐标，加上rand()的作用是保证不同粒子中同一新建站的位置不同但却大致在同一区域，以增强每一代不同粒子的多样性．

(3) 逐个判断 pL[j]，并设定距离 d2，计算第 j个负荷点和已经确定的 t个新站址间的距离，若这些距离都大于 d2，则该坐标可作为第 t+1个新站的位置值 pid_i[t+1]，即

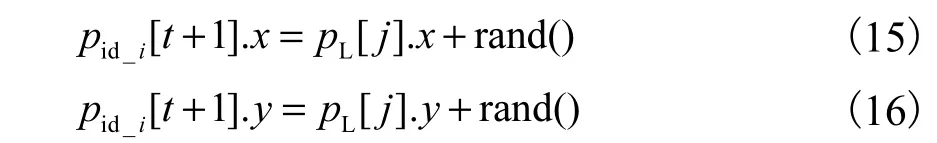
(4)重复上述过程，通过对负荷点的划分，最终确定每个粒子中所有需新建站的初始位置坐标．

3.5 变电站编码方式实现

若待规划区内的已有站和新建站在规划年的总个数为 n，而初始的粒子群个数为 N，则变电站基本信息的编码矩阵为

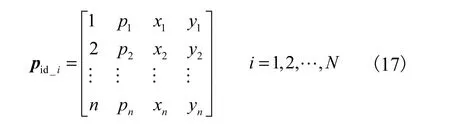
式中：pid_i为变电站规划方案，矩阵中 pi表示规划变电站 i的容量；xi和 yi为规划变电站的位置坐标．通过这个矩阵形式，可以清晰地反映规划方案中变电站的相关信息．

3.6 变电站供电范围划分

步骤 1初始化规划区内已有站和新建站的容量、位置坐标，进行第3.5节中的变电站编码，并统计规划区内负荷值及其坐标；

步骤 2按照式(5)，计算规划区内每一个负荷与每个变电站之间的线路长度；

步骤 3对计算后的线路长度进行从小到大的排序，从而形成新的线路长度数组；

步骤 4将排序后的线路长度数组与排序前进行对比，若排序后的线路长度值的第 i项(i＝1，2，…，M，M为变电站的数量)等于排序前的线路长度值，则转入步骤5；

步骤 5若累加后的负荷值不超过该变电站的容量，则将其划归该变电站的供电范围，否则 i＝i+1，继续执行步骤4；

步骤6计算下一个负荷点；

步骤7至所有负荷点均归入变电站供电范围结束.

4 算例分析

4.1 算例基本情况

算例区域为某城市开发区，总面积为 38.7,km2，远景负荷预测为 887.7,MW，现状具有变电站 1座，容量100,MVA(2×50,MVA)，目标年扩容1台主变，总容量变为 150,MVA(3×50,MVA)．表 1给出了算例的中压线路投资费用，表2给出了待选变电站容量类型及其投资费用．其中贴现率取0.1．

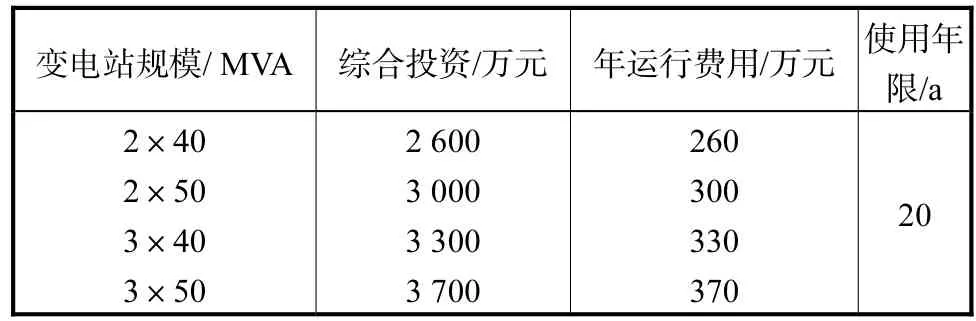
表2 变电站类型及其投资费用Tab.2 Types of substation and its cost

4.2 算例分析

分别采用文献[17]方法和本文算法对上述算例进行了分析对比，结果分别如图3和表3所示．

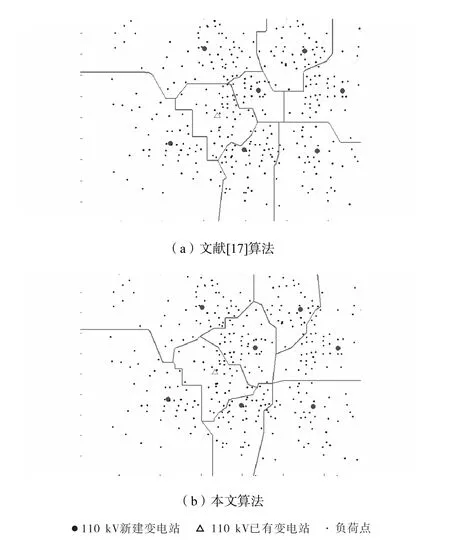
图3 2种算法的规划结果比较Fig.3 Results comparison of two algorithms

表3 2种算法的规划结果比较Tab.3 Results comparison of two algorithms

由表 3可知，利用本文算法与文献[17]算法的计算结果均选择了新建 7做变电站，但在新建站总容量、新建站容量组合等方面存在不同．相比之下，本文算法的新建变电站总容量有所降低，从而节省了21.8万元的新建变电站年费用．另一方面，由于本文算法在新建变电站选址以及供电范围划分等方面的优势，与文献[17]相比节省了 13.9%的线路投资及网损年费用．通过上述对比结果验证了本文算法在费用函数方面具有一定优势．

5 结 语

充分利用文化算法寻优质量高与粒子群算法寻

优速度快的特点，将 2种算法紧密结合，形成一种新的粒子群文化算法．在此基础上，将这种新算法应用于变电站优化规划问题的求解，不仅设置了新的编码方式，还在求解过程中提出了新建变电站个数与容量、供电范围等问题的解决方案，从而保证了寻优策略的实现．最终通过算例分析，验证了本文算法相比传统算法具有更好的效果．

［1］ 天津大学电力与能量系统研究所. 城市电网规划计算机辅助决策系统[R]. 天津：天津大学电气与自动化工程学院，1995.

Power and Energy Systems Institute of Tianjin University．Computer Decision Support System of Urban Electric Power Network Planning[R]. Tianjin：School of Electrical Engineering and Automation，Tianjin University，1995(in Chinese).

［2］ Lakervi E，Nurmi M. Present status in applying mathematical planning methods in AM/FM/GIS system[C]//Proceedings of International Conference on Electricity Distribution-CIRED. Birtningham，UK，1997：2-5.

［3］ Sun D I，Farris D R，Cote P J，et al. Optional distribution substation and primary feeder planning via the fixed charge network formulation[J].IEEE Trans on Power Apparatus and Systems，1982，101(3)：602-609.

［4］ Aoki K，Nara K，Sutoh T，et al. New approximate optimization method for distribution systems planning[J].IEEE Trans on Power Systems，1990，5(1)：126-132.

［5］ 杨丽徙，王家耀，贾德峰，等. GIS与模糊模式识别理论在变电站选址中的应用[J]. 电力系统自动化，2003，27(18)：87-89.

Yang Lixi，Wang Jiayao，Jia Defeng，et al. Application of GIS and fuzzy pattern recognition theory in substation locating[J].Automation of Electric Power Systems，2003，27(18)：87-89(in Chinese).

［6］ 葛少云，李 慧，刘 洪，等. 基于加权 Voronoi图的变电站优化规划[J]. 电力系统自动化，2007，31(3)：29-34.

Ge Shaoyun，Li Hui，Liu Hong，et al. Substation optimization planning based on the weighted Voronoi diagram[J].Automation of Electric Power Systems，2007，31(3)：29-34(in Chinese).

［7］ Liu Hong，Ge Shaoyun. Reactive power optimization based on improved particle swarm optimization algorithm with boundary restriction[C]//Proceedings of The Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies. Nanjing，China，2008：1365-1370.

［8］ 刘 洪，葛少云，李 慧. 基于硬约束调节的改进粒子群无功优化[J]. 天津大学学报，2009，42(9)：796-801.Liu Hong，Ge Shaoyun，Li Hui. Reactive power optimization based on improved particle swarm optimization algorithm with hard restriction regulation [J].Journal of Tianjin University，2009，42(9)：796-801(in Chinese).

［9］ Eberhart R C，Shi Y. Particle swarm optimization，developments，applications and resources[C]//Proceedings of the IEEE Congress on Evolutionary Computation.Piscataway，USA，2001：81-86.

［10］ Shi Yuhui，Eberhart R. A modified particle swarm optimizer[C]//Proceedings of IEEE International Conference on Evolutionary Computation. Alaska，USA，1998：69-73.

［11］ Durham W.Co-evolution：Genes，Culture，and Human Diversity[M]. Stanford：Stanford University Press，1994.

［12］ Renfrew A C.Dynamic Modeling in Archaeology[M].Edinburgh：Edinburgh University Press，1994.

［13］ Reynolds R G. On modeling the evolution of Hunter-Gatherer decision-making systems[J].Geographical Analysis，1978，10(1)：31-46．

［14］ Reynolds R G. An Adaptive Computer Model of the Evolution of Agriculture for Hunter-Gatherers in the Valley of Oaxaca，Mexico[D]. Ann Arbor：University of Michigan，1979.

［15］ Reynolds R G. An introduction to cultural algorithms[C]//Proceedings of the Third Annual Conference on Evolutionary Programming. San Diego，USA，1994：131-139.

［16］ 曾 涛. 基于粒子群文化算法的变电站规划研究[D].天津：天津大学电气与自动化工程学院，2008.

Zeng Tao. Research on Substation Planning Based on Particle Swarm of Culture Algorithm[D]. Tianjin：School of Electrical Engineering and Automation，Tianjin University，2008(in Chinese).

［17］ Dai Hongwei，Yu Yixin，Huang Chunhua，et al. Optimal planning of distribution substation locations and sizes-model and algorithm[J].International Journal of Electrical Power and Energy Systems，1996，18(6)：353-357.