基于粒子群-投影寻踪和遗传-神经网络集成的预测模型*
2012-05-10刘合香简茂球
刘合香 ,简茂球
(1.广西师范学院数学科学学院,广西 南宁 530023;2.中山大学环境科学与工程学院大气科学系,广东 广州 510275)
近30年来,非线性智能计算方法被广泛应用于数学、大气、经济、物理化学等学科[1-4]。随着非线性智能计算方法的不断发展,各种线性和非线性因子处理方法以及各类非线性模型,已越来越多地被人们所认识,尤其是如何选择适当的因子处理方式与建立的数学模型进行优化组合,是改进预测模型、提高预测精度的重要途径。Jin 等[5]针对神经网络方法在预测建模中存在的“过拟合”(over fitting)现象和提高泛化性能(gentralitation capability)问题,提出了采用主成分分析构造神经网络低维学习矩阵的预测建模方法。Yao等[6]针对季风指数具有显著的非线性变化特点及采用一般人工神经网络方法进行预测建模难以客观确定预测模型的网络结构问题,采用非线性遗传神经网络集成预测建模方法进行了月季时间尺度的季风强度指数预测方法研究。吴建生等[7]针对于BP神经网络在实际预测应用中,网络结构难以确定以及网络极易陷入局部解问题,提出一种基于神经网络的粒子群集成学习算法的预测模型。万中英等[8]分析了遗传算法和粒子群算法的优缺点,将两者有效地结合在一起,建立了遗传-粒子群的投影寻踪模型,解决了投影方向的寻优问题。
然而,上述这些方法在因子处理的控制过程中,或采取线性的自然正交展开方法、或采用粒子寻踪方法,都难以全面提取因子中所含的线性和非线性的信息。本文通过研究自然正交展开、粒子群-投影寻踪和遗传-神经网络模型的特点,利用自然正交展开和粒子寻踪,将高维非线性的数据,投影到低维空间,浓缩并析取高维非线性数据的线性和非线性信息,再将其作为遗传-神经网络集成预测模型的输入,构建一种新的非线性预测模型,并将该模型应用于影响华南台风频数预测试验。
1 预测因子的两种降维计算方法
在进行预测建模研究时,本文尝试对选择的预测因子进行线性降维(自然正交展开)和非线性降维(粒子群-投影寻踪),同时进行预测信息的挖掘计算。
1.1 自然正交展开降维计算方法
自然正交展开是一种可以将多维向量空间场资料压缩到少数几个主要模态的特征提取方法,主要包括以下步骤:
1)设预测因子距阵
(1)
将(1)分解成时间函数Z和空间向量V两部分:
X=VZ
(2)
V是列向量构成的特征向量矩阵,Z是所有主成分序列为行向量构成的矩阵。
2)计算协方差矩阵
(3)
其中,XT为X的转置。
通过计算实对称矩阵S的特征值λ1,λ2,…,λm(λ1≥λ2≥…≥λm)和特征向量V=(v1,v2,…,vm),各主成分为原因子变量的线性组合为:
ξi=υi1x1+υi2x2+···+υinxn
(4)
3)进一步标准化主成分:
Z=VTX=(ξ1,ξ2,···,ξn)T
(5)
采用上述主成分计算方法,将原来的大量因子压缩成少数几个与预测量相关高的主成分因子,将此作为预测模型输入的一部分。
由于变量ξi与ξj是相互独立的,从而协方差Cov(ξi,ξj)=0,进而,相关系数ρ(ξi,ξj)=0,说明变量ξi与ξj不相关,即主成分各因子变量之间是正交的,所以不会产生复共线性影响。
1.2 粒子群-投影寻踪计算方法
投影寻踪是用来处理高维空间里一些非正态分布和非线性数据的统计方法。它能够寻找反映高维空间数据的结构或特征的投影方向,将高维数据投影到低维空间,达到在低维空间研究和分析高维空间数据的目的。以往的研究[9-11]都是采用遗传算法寻找最佳的投影方向,但遗传算法对初始种群的选择有一定的依赖性,而且收敛速度慢,可行解不一定是最优解。粒子群优化(Particle Swarm Optimization, PSO)算法是由Kennedy and Eberhart于1995年提出的全局优化进化算法[12-13],Bonabeau et al.[14]通过对蚁群的研究,完善了该算法。该算法中有一个被优化函数决定的适应值,根据每一个粒子的位置和速度决定搜索方向,各个粒子通过相互之间的作用,记忆、追随当前的最优粒子,在解空间中不断地搜索复杂空间的最优区域,如果找到较好的解,将会以此为依据来寻找下一个解。用粒子群算法优化投影方向的具体过程如下:
设预测的因子矩阵如式(1),投影方向矩阵为:
R={rij;i=1,2,…m,j=1,2,…p}
(p (6) 通过 Z=X·R={zij;i=1,2,…,n,j=1,2,…,p} (7) 把原数据综合成低维子空间的数据。通过计算投影值的标准差 (8) 和投影值的局部密度: ·u(t)·(K-dij) (9) 进一步构造投影指标函数: QR=Sz·Dz (10) 从而使局部投影点密集并凝结成团,以确定投影方向。 由于传统方法难以求解复杂的非线性优化问题,所以,定义粒子群算法的适应度函数 Fit(rij)=QR (11) 利用粒子群优化算法求解投影方向: maxQR=Sz·Dz rj≥0 (12) 具体实施如下: ① 初始化粒子群。每个粒子看作解空间的一个点,在[0,1]上随机产生N个随机数作为个体,用m×p个浮点数表示粒子位置和速度的投影系数矩阵; ②通过式(11)和(12),计算每个粒子的适应度Fit(rij),设第i(i=1,2,…,N)个粒子的速度为Vi,位置为Xi,它经历的最好位置为pb(i),群体中最好粒子的位置为pgb(i); ③对每个粒子,用它的适应度Fit(rij)与个体所经历的最好位置的适应度pb(i)比较,如果Fit(rij)>pb(i),就用Fit(rij)替换pb(i);然后,用Fit(rij)与全局所经历的最好位置的适应度pgb(i)比较,如果Fit(rij)>pgb(i),用Fit(rij)替换pgb(i); ④根据粒子进化方程: Vi+1=ω·Vi+c1r1[pb(i)-Xi]+c2r2[pgb(i)-Xi]Xi+1=Xi+Vi+1 更新第i(i=1,2,…,N)个粒子的速度和位置。其中,c1,c2为学习因子,r1,r2是[0,1]间的随机数,ω为惯性权重; ⑤ 重复②-④步,直至适应度达到进化代数的要求; ⑥ 从进化到最后一代中选取k个适应度较高的个体,得到k个较优投影方向R={rij,i=1,2,…,n,j=1,2,…,k},新的因子矩阵为: (13) 遗传-神经网络集成预测模型是采用进化计算的遗传算法和人工神经网络技术集成的模型构建方法[6,15-16]。其主要思想和过程是利用进化计算的遗传算法结合神经网络技术生成m个(数10个)神经网络模型,然后利用每个预测模型个体的预测结果做集成,得到最终的集合预测结果。集合预测个体的神经网络模型是采用较为通用的三层前馈网络模型[17-18]。该网络模型的基本算法可以归结为: 1)随机给出网络模型输入层到隐层,隐层到输出层的连接权和阈值,设定模型的总体收敛误差,利用式(14): γhi+θi) (14) 计算输入层到隐含层的激励值(bi),其中rhi为输入层到隐含层的连接权,ah为相应的输入样本,θi为相应的阈值。进一步利用式(15): ηj) (15) f(x)=1/(1+e-x) (16) 2)根据学习矩阵样本,对网络进行学习训练,计算由式(15)得到的模型输出与期望输出的误差,并调整输入层到隐含层和隐含层到输出层的连接权系数、阈值。 3)当模型的计算收敛误差大于设定的收敛误差时,转到b,否则学习结束,并根据网络模型的连接权、阈值和预测样本的输入因子,得出模型输出值。 上述计算过程简单给出了作为集合预测个体的单个神经网络模型的学习过程。而如何构造m个神经网络模型个体,本文是采用了进化计算的遗传算法(Genetic Algorithms)[15,18]。该算法是一种由选择(繁殖),交叉(重组)和变异(突变)三个遗传算子组成的全局搜索进化算法。由遗传算法生成神经网络集合个体的计算主要可归结为3个部分: 1) 采用二进制和实数的混合编码方法,将每个神经网络预测模型个体的连接权,阈值按顺序排成一串,形成一个染色体作为一个遗传个体。初始时段,采用随机数生成m个神经网络遗传个体,得到一个用于进化计算的神经网络预测模型遗传种群。 2)通过对遗传种群个体解码,利用前面的式(14)和式(15)计算遗传种群中每个神经网络个体输入层到隐层的输出和隐层到输出层的输出值。进一步利用: (17) 计算各个神经网络个体的总体误差。并将总体误差的倒数定义为适应度函数: (18) 3)对由随机数生成的初始遗传种群(设由m个遗传个体组成遗传种群),采用选择,交叉和变异三个遗传算子,对初始遗传种群进行进化计算操作,其中,① 选择算子操作:该算子是采用轮盘选择方法,先将遗传种群的每个个体解码,并根据式(18)计算每个遗传个体的适应度值,再计算出全部遗传个体的适应度总和以及每个遗传个体被选择的概率: (19) 以保证在轮盘选择中具有较大适应度的遗传个体有更大的可能被遗传到下一代。 ② 交叉算子操作:交叉算子操作是采用多点交叉方法,它是对经过选择算子操作后,除了被选择操作算子选择到下一代遗传种群以外的其它遗传个体,以交叉概率pc对遗传个体作多点交叉的基因变换,形成新的遗传个体。 ③ 变异算子操作:变异算子也是对轮盘选择,选择下一代遗传种群以外的其它遗传个体,以概率pm对遗传个体的基因与另一个遗传个体作等位基因替换形成新的遗传个体。 利用以上3个遗传算子对初始遗传种群进行进化计算,形成新一代遗传种群。并以此进行反复的进化计算,每进行一次进化计算,遗传种群就进化一代,一直进化到预先设定的第N代,进化计算结束。将遗传种群的每个遗传个体解码,得到m个神经网络模型个体,这m个模型个体即为集合预测的集合个体。本文采用等权方法,对m个集合个体成员赋予相同的权重,进行集合预测建模,即对每一个神经网络个体赋予相同的权重,将m个神经网络预测模型的预测值作累加并计算平均值,得出遗传-神经网络集合预测模型的集合预测值。 大量的研究和实践表明,预测对象和预测因子之间存在着十分复杂的线性和非线性关系,因此,要提高预测模型的精度,既要设法提取和浓缩原始因子序列中所包含的线性信息,同时,也要析取其中的非线性信息。通过自然正交展开,可以较好地提取和浓缩原始数据中的线性信息,而粒子寻踪则具有提取和浓缩非线性信息的特点。综合以上两种方法,可以较为全面地提取和浓缩原始数据序列中的有用信息。此外,非线性模型的泛化性能也是评价模型优劣的另一关键因素。与普通的神经网络预测模型不同,遗传-神经网络集成数学模型,不仅可以客观地确定网络结构,还具有非常好的泛化性能。 鉴于自然正交展开、粒子寻踪以及遗传-神经网络集成模型的优点,提出基于粒子寻踪和遗传-神经网络集成相结合的非线性预测模型,建模的具体步骤:① 对原始数据进行标准化处理,形成新的数据序列。② 将标准化处理后形成的新数据序列进行自然正交展开,提取若干因子。③同时,通过粒子寻踪对标准化处理后形成的新数据序列做降维处理,提取若干因子。④将第②③步得到的因子作为遗传-神经网络集成模型的输入。⑤ 进行遗传-神经网络集成训练,并建立数学模型。 华南沿海(广东,广西和海南省沿海)是我国沿海热带气旋活动最频繁、出现个数最多、影响程度最严重、全年受影响期最长的区域之一。但年影响的频数变幅大,最多时9个,最少时1个。影响频数的因子与频数存在十分复杂的线性和非线性关系,很多学者提出了许多预测模型[15,19-21],但是,目前尚未见有利用粒子群-投影寻踪算法将高维空间上的因子进行逐次降维计算,进一步利用非线性人工智能技术建模,进行台风频数预测的研究工作报道。本节应用上一节所构造的模型进行华南台风频数的遗传-神经网络预测试验,探索台风频数预测的新方法。 本文研究的数据来源于台风年鉴(1949-1988年)和热带气旋年鉴(1989-2009),选取了1949-2009年影响华南的台风频数。并以1949-2004年56个样本作为预测的建模样本,2005-2009年5个样本作为独立的预测样本。 以NCEP再分析资料的500 hPa月平均高度场及月平均的海温场作为基本的预测因子场。统计计算了台风频数序列与前期(当年1月至5月,上一年6-12月)各月预测因子场的相关关系。以台风频数与前期各月预测因子场的相关系数绝对值≥0.20(达到0.02相关显著性水平)的格点作为一个预测因子区,再对相关区内的格点进行自然正交展开,进一步计算台风频数与自然正交展开后各分量的相关关系,提取高相关的各主分量,保证预测因子的高相关性。表1给出了台风频数序列(样本长度为56)与月平均海温、月平均500hPa的高度场前期各月相关普查计算后的高相关预测因子区,进行自然正交展开后计算得出的台风频数与各主分量的相关系数,取相关系数绝对值≥0.20的27个(其中海温场的5个,500 hPa高度场22个)初选因子做建模样本和预测试验。 表1 两个物理量场高相关区自然正交展开后各主分量与台风频数的相关系数 对上述27个因子采用逐步回归方法,取F=3,从27个因子中筛选出9个因子,再对这9个预测因子作自然正交展开计算,并以方差贡献大(分别是18.73%、15.6%、11.36%)、且与预测量相关高(分别为0.62、-0.36和0.26)的3个主分量作为预测因子。同时,为了进一步有效挖掘预测因子的有用预测信息,再对27个因子中筛选的9个因子采用粒子群优化投影方法逐次降成1维(1维预测因子与预测量的相关系数为0.204)。利用3个主分量预测因子和1个粒子群投影寻踪降维因子共4因子作为模型输入,采用前面第3节的遗传-神经网络集成预测建模方法建立台风频数的预测模型。其中进化计算的遗传种群数取100,进化代数为100代,遗传操作的交叉概率为0.9,变异概率取0.05,加权系数下限取0.1、上限取0.9,投影维数取3,学习因子取1.5,位置下限取0、上限取1,速度下限取0、上限取1。并以神经网络输入节点的0.5~1.5倍作为网络模型结构的搜索空间。网络训练次数为200次,进化计算结束后,对100个遗传个体解码,得到100个神经网络集成预测个体,再采用平均集成算法,得到台风频数的遗传-神经网络集成预测模型。利用该预测模型,对2005-2009年进行了逐年的独立样本的预测试验,预测结果见表2。由表2可以看出,这种新建的预测模型对台风频数有较好的预测效果,5 年预测的平均绝对误差为0.81个,相对误差为13%。 表2 基于自然正交展开和粒子寻踪的遗传-神经网络集成的台风频数预测结果 本文提出的台风频数预测方法,在前期物理量预测因子处理方法和预测模型输入的设计构造上进行了新的尝试,这种新的设计和计算处理方法是否有优越性,需要作进一步的分析比较。首先,分析在遗传-神经网络的集合预测模型输入中,如果不采用粒子群优化投影方向,将高维非线性数据投影到低维空间,来构造台风频数系统的影响因子,而是利用月平均海温场、500 hPa高度场经过自然正交展开后得出的3个主分量预测因子,作为集合预测模型输入,同样建立一个遗传-神经网络的台风频数预测模型。并且在预测建模过程中,进化计算的遗传种群数等各项参数全部与3.2节一样。利用该预测模型同样对2005-2009年5年独立样本作预测试验。预测结果见表3。由表3结果可以看到,该预测模型的5 a独立样本预测平均绝对误差为1.10,平均相对误差为0.22,预测误差明显大于3.2节表2的预测结果。由此对比分析可以看出,用粒子群投影寻踪降维方法进一步挖掘预测信息是有效的。 表3 基于自然正交展开的遗传-神经网络集成的台风频数 另外,为了更进一步客观地分析评价预测模型输入的降维处理计算方法和遗传-神经网络集成预测模型的预测性能,将这种预测建模方法与常规的逐步回归预测建模方法进行了预测比较试验。首先仍然以前面计算得出的月平均海温场5个相关因子区, 500 hPa月平均的高度场22个相关因子区,共27个高相关预测因子作为初选预测因子。为了作客观的比较,根据这27个预测因子我们分别取F=2、3、4、5时,由逐步回归方法自动从这27个预测因子中筛选出13个,10个,9个和6个预测因子建立4个逐步回归预测方程(预测方程的建模样本长度同样为56)。分别用这4个回归方程对2005-2009年5年的独立样本进行预测试验。从表4的结果可以看出,采用常规的逐步回归预测方法和选择预测因子的方法,所建立的预测模型,其独立样本的预测精度均明显差于本文提出的这种新的预测因子处理和预测建模方法。进一步对比分析可以看出,在4个逐步回归方程中,对5年独立样本预测精度最高的是F=4时10个预测因子的回归方程,其5年独立样本的平均绝对误差为0.92 ,平均相对误差为0.17,误差明显大于表3的0.81和0.13。而4个回归方程中预测最差的(F=5,6个因子的预测方程)方程对5年独立样本的预测平均绝对误差和相对误差,更是达到2.52和0.42。另外,当F=3时,逐步回归方程选出的9个预测因子,就是表2和表3预测方法依据的相同的9个预测因子。从结果比较可以看出,相同的9个预测因子,采用回归方法,同样5年的独立样本预测平均绝对误差和平均相对误差分别为1.19和0.19,误差明显偏大。而从总体的对比分析可以看到,4个逐步回归方程所依据的初选得出的27个预测因子与表2预测模型所依据的预测因子是完全一样的,4个回归方程也完全是客观计算得到的。因此,可以看出,由本文提出的这种预测因子的计算处理方法和预测建模方法,在预测初选因子相同,独立预测样本相同情况下,预测精度是有明显提高的。这表明本文提出的这种预测因子的处理方法,对于挖掘预测因子的预测信息,提高预测模型的预测性能是十分有益的。 表4 逐步回归方法预测模型的台风频数预测结果1) 本文根据预测对象和预测因子存在复杂的线性和非线性关系的特点,在数学建模上,通过自然正交展开的线性降维计算处理和粒子群-投影寻踪方法的非线性预测因子降维处理,将高维非线性数据投影到低维空间,构造遗传-神经网络集合预测模型,对华南台风频数进行了预测试验,并进一步将预测结果与常规的线性统计预测方法进行了对比分析。结果表明,本文提出的这种新的非线性集合预测模型,比常规方法预测效果均有明显的改进,主要是因为这种新的预测建模方法,不仅能从预测因子中,充分挖掘初选预测因子的有用预测信息,为预测模型提供更多有用的预测信息。并且在预测建模方法上,采用的遗传-神经网络集成预测方法,该方法的激励函数为非线性Sigmoid函数,这种非线性预测方法可能比线性的逐步回归方法更适合台风频数的非线性年变化特征。本文为进一步探索研究其他预测对象(如自然灾害、经济金融等领域)预测建模提供了新的思路和方法,但是由于采用自然正交展开和粒子群算法与投影寻踪方法相结合来挖掘预测因子的预测信息是一种有效的新尝试,如何合理地确定粒子群-投影寻踪降维的维数还需要依据不同预测对象作进一步深入研究。 参考文献: [1]赵占芸,罗跃虎,沈世镒.特征向量计算的神经网络方法[J].应用数学学报,2000,23(2):233-239. [2]TANG Y,HSIEH W.Coupling neural networks to incomplete dynamical systems via variational data assimilation[J].Mon Wea Rev,2001,129(4): 818-83. [3]苏顺华,苏顺兵.中国上市公司企业规模的模糊神经网络模型设计[J].模糊系统与数学,2007,21(1):150-158. [4]邓勇,杜志敏,陆燕妮.神经网络优化组合预测模型在油气产量预测中的应用[J].高校应用数学学报,2008,23(1):1-6. [5]JIN L,KUANG X Y,HUANG H H.Study on the overfitting of the artificial neural network forecasting model[J].Acta Meteorologica Sinica,2005,19(2): 90-99. [6]YAO C,JIN L,ZHAO H S.Ensemble prediction of monsoon index with a genetic neural network model[J].Acta Meteorologica Sinica,2009,23(6):701-712 . [7]吴建生,刘丽萍,金龙.粒子群-神经网络集成学习算法气象预测建模研究[J].热带气象学报,2008,24(6):679-686. [8]万中英,廖海波,王明文.遗传-粒子群的投影寻踪模型[J].计算机工程与应用,2010,46 (20): 210-212,240. [9]刘合香,徐庆娟.区域洪涝灾害风险的模糊综合评价与预测[J].灾害学,2007,22(4): 38-42. [10]刘合香,徐庆娟.基于r维正态扩散的区域热带气旋灾害模糊风险分析[J].数学的实践与认识,2011,41(3):150-159. [11]LIU H X,ZHANG D L.Analysis and prediction of hazard risks caused by tropical cyclones in Southern China with fuzzy mathematical and grey models[J].Applied Mathematical Modelling.doi:10.1016/j.apm.2011.07.024 36 (2012) 626-637. [12]KENNEDY J,EBERHART R C.Particle swarm optimization[C]//Pro IEEE International Conference on Neural Networks Vol.IV:1942-1948.IEEE Service Center,Piscataway,NJ,1995. [13]EBERHART R C,KENNEDY J.A new optimizer using Particle swarm theory[C]//Proceedings of the Sixth International Symposium on Micro Machine and Human Science: 39-43.IEEE service center,Piscataway,NJ Nagoya,Japan,1995. [14]BONABEAU E,DORIGO M,THERAULAZ G.Inspiration for optimization from social insect behavior[J].Nature,2000,406(6):39-42. [15]姚才,金龙,黄明策等.遗传算法与神经网络相结合的热带气旋强度预报方法试验[J].海洋学报,2007,29(4):11-19. [16]金龙,吴建生,林开平等.基于遗传算法的神经网络短期气候预测模型[J].高原气象,2005,24(6):981-987. [17]周明,孙树栋.遗传算法原理及应用[M].国防工业出版社,2002. [18]JIN L,JU W M,LIAO Q L.Study on Ann-based Mutti-step Prediction Model of Short-term Climate Variation[J].Advances in Atmospheric Sciences,2000,17(1): 157-164. [19]尹宜舟,罗勇,GEMMER Marco,等.基于BP神经网络技术的西北太平洋热带气旋年频数预测[J].热带气象学报,2010,26(5):614-619. [20]陆虹,金龙,缪启龙,等.影响广西热带气旋年频数的神经网络预测模型[J].南京气象学院学报,2003,26(1):56-62. [21]应明,万日金.影响我国的热带气旋年频数预测[J].应用气象学报,2011,22(1):66-76.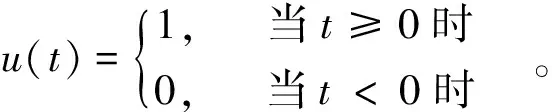
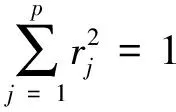

2 非线性预测模型的构建
2.1 遗传-神经网络集成预测模型

2.2 基于粒子群-投影寻踪和遗传神经网络集成的预测模型
3 实例分析与比较
3.1 数据来源与数据处理

3.2 华南台风频数的预测试验
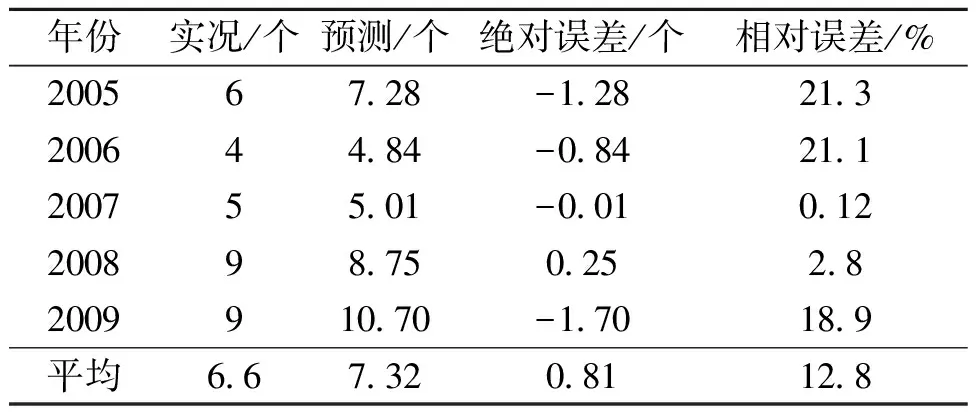
3.3 预测模型的性能分析

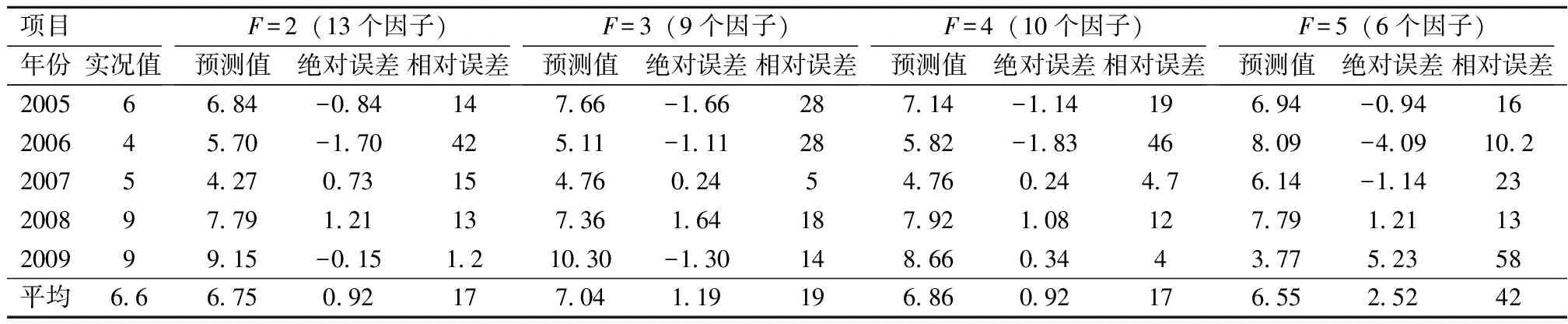
4 结 论
