C－Bézier曲线显式降阶算法

周联

(上海海事大学 文理学院，上海 201306)

0 引言

近年来，C曲线曲面方法［1－3］作为一种新的曲线曲面造型理论，引起广大几何设计工作者的密切关注，其主要优点［4］在于它兼备有理Bézier曲线或有理B样条曲线能统一表示圆锥曲线和自由曲线的长处，且能摆脱有理曲线曲面在微分运算和积分运算上较为繁琐的困境.因而，有关C曲线曲面的几何性质、几何计算、几何逼近的研究［5－9］，在一定程度上成为国内外计算机辅助几何设计学术界的研究热点.

目前，在C曲线曲面的理论探索与实用技术开发上，一个值得注意的动向是大部分研究偏重于其几何性质和几何表示方面，但在几何计算和几何逼近方面相对滞后.事实上，几何计算和几何逼近方法对工程应用显得更为重要、现实.例如，在Bézier曲线的几何逼近方面，国际上众多学者已经对降阶课题作了多年的深入研究［10－21］，并且将 Bézier曲线降阶方法推广到曲面［22－24］，但C曲线降阶的研究论文却寥若晨星.赵林玉［8］应用广义逆矩阵理论和扰动约束法分别给出两种降阶逼近算法:前者考虑端点高阶插值的一次降多阶情形，但其逼近误差比较大;后者由于C－Bézier曲线退化条件的复杂，事实上只给出将4次曲线降为3次的特殊算法.此外，赵林玉［8］把曲线的广义逆矩阵方法推广到C－Bézier曲面的约束降阶.林新辉［9］讨论 C－Bézier曲线在 L2范数下的保持端点C1，C2，G1，G2约束降1阶逼近，但没有考虑到一次降多阶情形.由此可见，研究并开发优质高效的C曲线降阶算法是当务之急.所谓优质，是指算法必须满足一次性降多阶、保端点高阶连续、精度最高、显式表示;所谓高效，是指算法必须稳定且速度最快.

基于文献［9］的基转换矩阵，本文利用分而治之的思想，首先把端点高阶插值的C曲线最佳降多阶这一复杂问题分解为两个简单问题——仅有端点高阶插值但无须降阶，以及无须端点插值的最佳降多阶;其次，利用 C－Bézier基函数在空间 Γn=span{1，t，…，tn－2，sint，cos t}下的显式表示，结合最小二乘法，给出C－Bézier曲线保端点高阶插值的显式最佳降多阶算法.

1 预备知识

1.1 基函数的定义

设定初始函数:

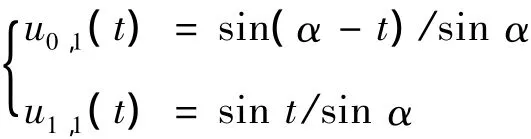
式中:t∈［0，α］.在空间 Γn=span{1，t，…，tn－2，sin t，cos t}上采用递归的方法构造 n次 C－Bézier基函数{u0，n(t)u1，n(t)… un，n(t)}，定义［3］

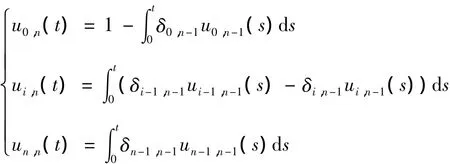
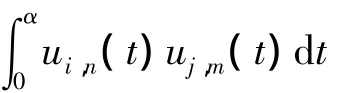
引理1 n次C－Bézier基函数在基{1 t …tn－2sin t cos t}下的显式［9］表示为

式中:Un(t)=(u0，n(t)，u1，n(t)，…，un，n(t));Tn(t)=(ti，n)1×(n+1)=(1，t，…，tn－2，sin t，cos t);Βn=(b0，n，b1，n，…，bn，n).

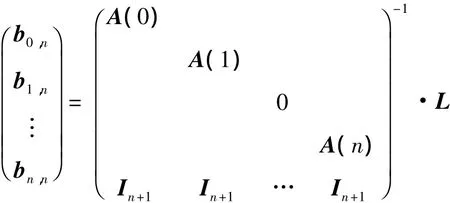
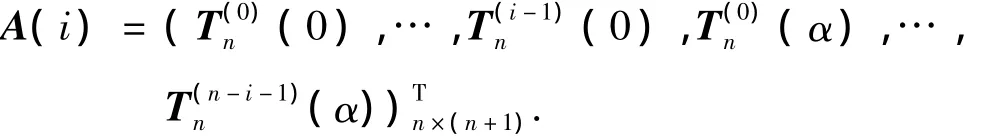
当0≤k≤n－2时，

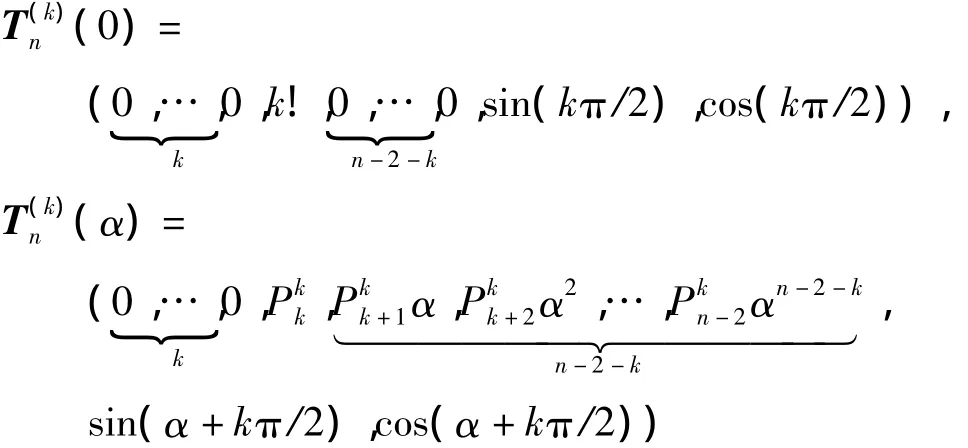
当k=n－1，n时，

根据引理1，易知:

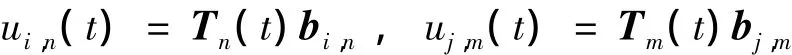
若记

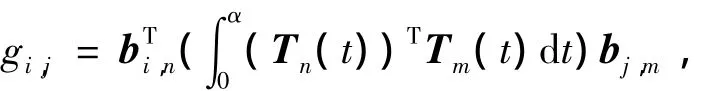
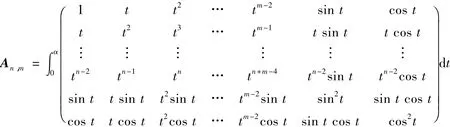
则

最后，令 Gn，m=(gi，j)(n+1)×(m+1).

Gn，n为实对称正定矩阵，所以它可逆.Gn，m只与降阶前后的阶数有关系，所以可以先把它们逐一计算出来，存入数据库中，以备随时调用.这可保障C－Bézier曲线降阶的高效率计算.通过下面6个积分公式，可以迭代求得矩阵Gn，m中的系数.

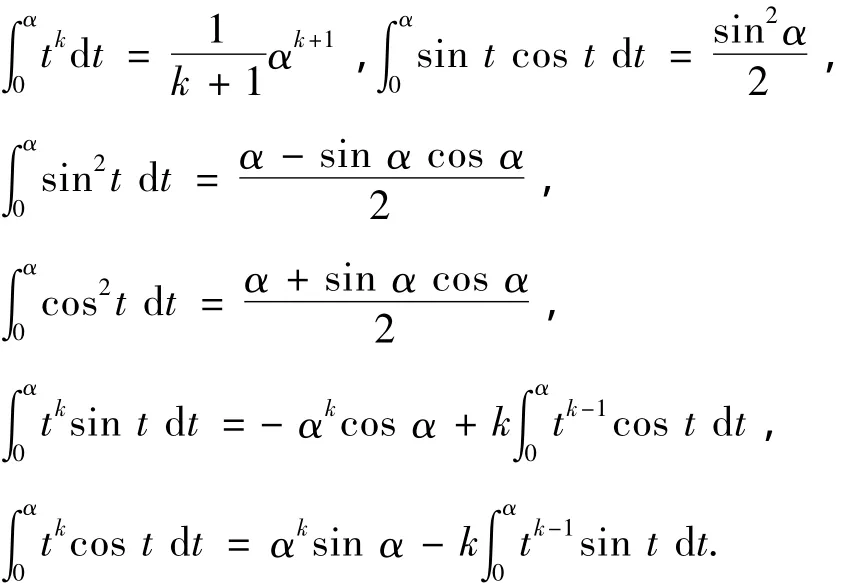
1.2 端点插值

给定控制顶点pi，可以确定一条C－Bézier曲线

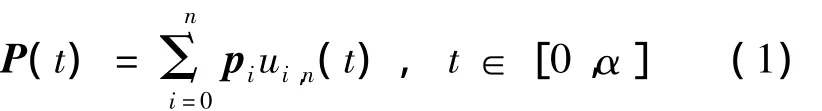
根据前述基函数定义，易知式(1)曲线的导矢曲线就是一条n－1次C－Bézier曲线，即

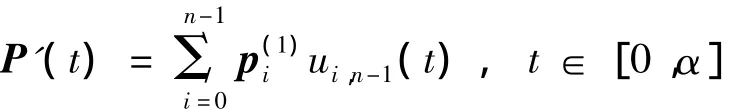
根据上面的导矢曲线形式，可以推出引理2.引理2 式(1)所示曲线P(t)在两端点上的(k，l)阶导矢分别为

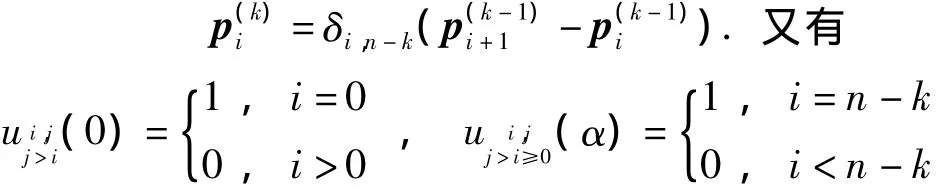
2 C－Bézier曲线显式约束降多阶

首先把式(1)所示的曲线改记为Pn(t).目标是找一条同样的带参数α但次数低达m(m＜n)的C－Bézier曲线

使得它与原曲线Pn(t)在两端点处保持(k，l)阶连续(k，l≥0;k+l≤m)，并且它们之间的最小二乘距离最小，即

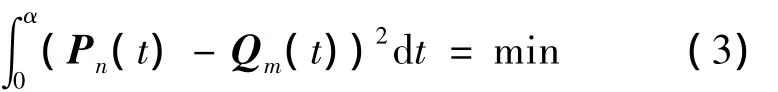
2.1 确定约束控制顶点

在工程应用中，两条拼接曲线在端点处往往需要保持高阶连续.为此，根据引理1导出降阶前后两条曲线的端点约束条件.

引理3 曲线Pn(t)和Qm(t)在两端点处分别保持(k，l)阶连续，则有

(1)对于t=0，

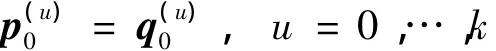
(2)对于t=α，

并且有

借助引理3，可求出降阶曲线Qm(t)的两端约束控制顶点 q0，q1，…，qk和 qm－l，…，qm.

2.2 确定无约束控制顶点

为得到Qm(t)的其余控制顶点(无约束控制部分)，下面将其全部控制顶点和相应的基函数全体分别分成两部分.先设指标集

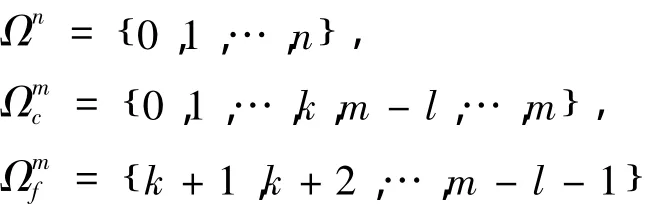
那么，可以写出

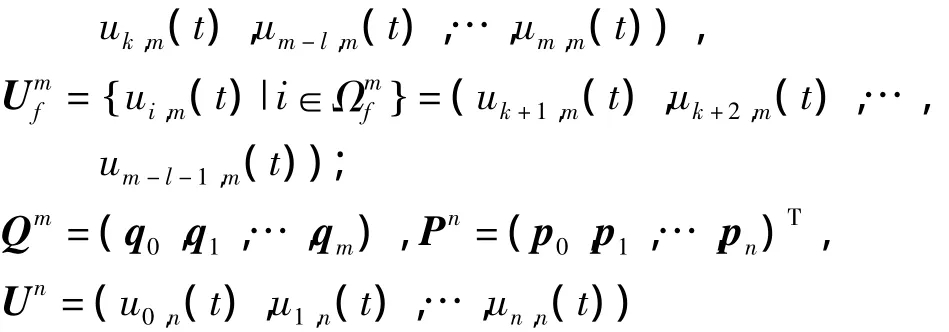
则问题(3)可以表述为

上式可写成矩阵形式

其中

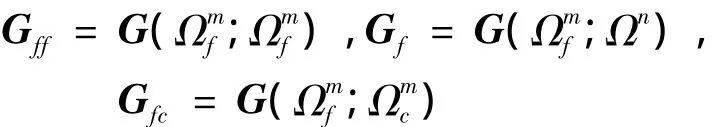
由于矩阵Gff为实对称正定，所以它可逆.因而欲求的降阶曲线的未约束控制顶点为

2.3 实例和比较

例1 采用文献［8］中例1的数据.已知原曲线的控制顶点为

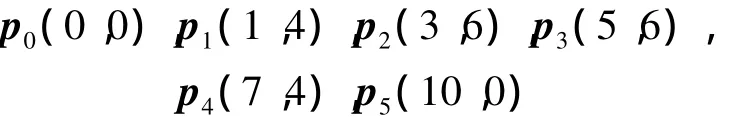
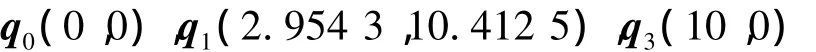
取α=π/4求保端点插值且降3阶的逼近曲线.采用本文方法所求得的降阶曲线控制顶点为其中，逼近误差为0.044 6.而采用文献［8］的方法所得到的逼近误差为0.089 7.

文献［9］只能每次降1阶，效率不高.图1给出原曲线(实线)和最佳降3阶逼近曲线(虚线).

图1 原曲线和最佳降3阶逼近曲线

例2 采用文献［9］中例4数据.已知原曲线的控制顶点为

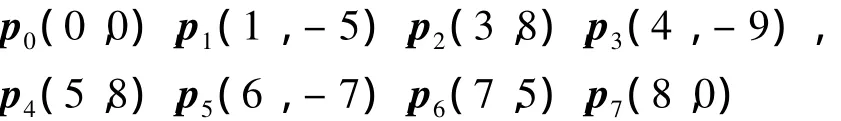
取α=π/3求保端点插值且降2阶的逼近曲线.采用本文方法所求得的降阶曲线控制顶点为q0(0，0)，q1(1.507 0，－ 4.681 2)，q2(4.443 6，8.523 7)，q3(4.895 8，－9.099 4)，q4(6.664 4，5.276 3)，q5(8，0)，逼近误差为0.100 5.而采用文献［8］的方法所得到的逼近误差为0.206 8.图2给出原曲线(实线)和最佳降2阶逼近曲线(虚线).

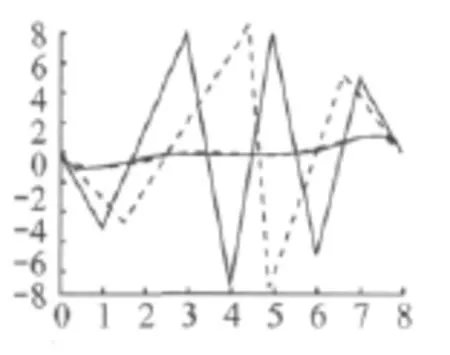
图2 原曲线和最佳降2阶逼近曲线

3 结束语

根据 C－Bézier基的显式表示，给出 C－Bézier曲线曲面的约束显式最佳降阶算法.

该算法有以下优点:(1)降阶曲线显式表示;(2)一次降多阶;(3)逼近误差最佳;(4)降阶曲线满足端点高阶插值.

该算法的不足之处是降阶逼近误差不能在曲线降阶之前先验性地求出，但由于降阶曲线的控制顶点是显式表示的，上述不足并不影响本算法的计算效率.

［1］ZHANG J W.C－Curves:an extension of cubic curves［J］.Comput Aided Geometric Des，1996，13(3):199－217.

［2］ZHANG J W.Two different forms of C－B－splines［J］.Comput Aided Geometric Des，1997，14(1):31－41.

［3］CHEN Q Y，WANG G Z.A class of Bézier－like curves［J］.Comput Aided Geometric Des，2003，20(1):29－39.

［4］FARIN G.Algorithms for rational Bézier curves［J］.Comput Aided Des，1983，15(2):73－77.

［5］MAINAR E，PENA J M.A basis of C－Bézier splines with optimal properties［J］.Comput Aided Geometric Des，2002，19(4):291－295.

［6］樊建华，邬义杰，林兴.C－Bézier曲线分割算法及G1并接条件［J］.计算机辅助设计与图形学学报，2002，14(5):421－424.

［7］YANG Q，WANG G Z.Inflection points and singularities on C－curves［J］.Comput Aided Geometric Des，2004，21(2):207－213.

［8］赵林玉.高阶C－Bézier曲线曲面性质研究及其应用［D］.南京:南京航空航天大学，2005.

［9］林新辉.C－Bézier曲线降阶逼近［D］.杭州:浙江大学，2005.

［10］WATKINS M，WORSEY A.Degree reduction for Bézier curves［J］.Comput Aided Des，1988，20(3):398－405.

［11］ECK M.Degree reduction of Bézier curves［J］.Comput Aided Geometric Des，1993，10(3):237－252.

［12］CHEN Guodong，WANG Guojin.Optimal multi－degree reduction of Bézier curves with constraints of endpoints continuity［J］.Comput Aided Geometric Des，2002，19(6):365－377.

［13］ZHANG Renjiang，WANG Guojin.Constrained Bézier curves’best multi－degree reduction in the L2－norm［J］.Progress in Nat Sci，2005，15(9):843－850.

［14］WOZ'NY P，LEWANOWICZ S.Constrained multi－degree reduction of triangular Bézier surfaces using dual Bernstein polynomials［J］.J Computational＆ Applied Math，2010，235(3):785－804.

［15］周联，王国瑾.带G1连续约束的Bézier曲线显式最佳降多阶［J］.计算机辅助设计与图形学学报，2010，22(4):735－740.

［16］RABABAH A，MANN S.Iterative process for G2－multi degree reduction of Bézier curves［J］.Applied Math ＆ Computation，2011，217(20):8126－8133.

［17］CHEN Xiaodiao，MA Weiyin，PAUL J C.Multi－degree reduction of Bézier curves using reparameterization［J］.Comput Aided Des，2011，43(2):161－169.

［18］康宝生，石茂，张景峤.有理Bézier曲线的降阶［J］.软件学报，2004，15(10):1522－1527.

［19］覃廉，关履泰.有理曲线曲面的降阶逼近［J］.中国图像图形学报，2006，11(8):62－69.

［20］江明，罗予频，杨士元.基于微粒群算法的有理Bézier曲线降阶［J］.计算机应用，2007，27(6):1524－1526.

［21］刘彬.基于遗传算法的NURBS曲线降阶［J］.计算机工程，2008，34(14):194－196.

［22］郭清伟，朱功勤.张量积Bézier曲面降多阶逼近的方法［J］.计算机辅助设计与图形学学报，2004，16(6):777－782.

［23］周登文，刘芳，居涛，等.张量积Bézier曲面降阶逼近的新方法［J］.计算机辅助设计与图形学学报，2002，14(6):553－556.

［24］ZHOU Lian ，WANG Guojin.Constrained multi－degree reduction of Bézier surfaces using Jacobi polynomials［J］.Comput Aided Geometric Des，2009，26(3):259－270.