塔里木盆地多种沙源类型沙通量异变特征研究
2012-05-07杨兴华艾力买买提明黄有志
霍 文,何 清,杨兴华,艾力·买买提明,黄有志
(1.中国气象局 乌鲁木齐沙漠气象研究所,乌鲁木齐830002;2.塔克拉玛干沙漠大气环境观测试验站,新疆 塔中841000;3.布尔津县气象局,新疆 布尔津836600)
众所周知,沙漠作为一种特殊的下垫面形式,通过大气动力的作用以及不同沙漠的局地微气候或者局地天气孕育了沙尘暴、浓浮尘、扬沙等灾害性天气,不断影响着周边以及下游地区。事实上,沙漠气候和沙漠天气对非沙漠地区以及全球的的综合影响是十分显著的。关于沙漠的研究国外有很多的先驱者,Aufrere于1928—1934年间利用当时可以收集到的气象资料,试图建立沙丘形态、走向与风况的关系,这是有关沙漠气象研究由定性向定量转变的初步尝试,虽然并不完善,却是重要的研究思想突破[1]。1929—1930年,Bagnold在利比亚沙漠中进行了人类最早的汽车沙漠考察,并从沙粒的运动特征着手进行研究[2],他于1935年在英国剑桥大学建立了第一个用于风沙研究的风洞,并创造性地应用和推广了流体力学原理,建立了风沙物理学,并著《风沙和荒漠沙丘物理学》(The Physics of Blown Sandand Desert Dunes)一书。随着国内外沙尘暴的广泛研究以及预报业务的客观需要,更多的预报模型得以开发,如前苏联科学家提出的波查罗夫(Bocharov)模型,德克萨斯理工大学提出的侵蚀分析模型(TEAM),澳大利亚科学家提出的风蚀评价模型(WEAM)、美国农业部的修正风蚀方程(RWEQ)和风蚀预报系统(WEPS)等。关于风蚀模拟的代表成果集中反映在《风蚀物理学及其模拟》(Physics and Modeling of Wind Erosion)一书中[3]。沙尘灾害预报质量和准确率的提高在于模式中起沙计算模块的不断改进,即物理化起沙参数的不断优化,起沙参数在不同的沙漠区域各异,需要大量的野外试验与理论相结合不断的更新和量化确定。目前,仍有许多学者致力于风蚀、地表起沙参数等方面的深入研究[4-15],但是地表起沙是一个极为复杂的物理过程,加之世界沙漠分布广泛,沙漠地区自然条件苛刻,不利于科学家深入研究,很多的研究局限于沙漠的外围或者个别沙漠腹地,因此地表起沙物理特性的研究还任重而道远。
同时,沙害问题依然是人们和全社会关注的重点,研究沙尘灾害的环境意义和社会效益不再赘述,实际上灾害性沙尘暴天气的预报工作才是气象科研工作者的重中之重,还需要有关精密的、确切的资料。沙尘天气过程中沙尘通量的准确计算是一个极为关键的地表起沙参数问题,目前的很多沙尘天气数值预报模式及起沙模式的计算值与实际值存在很大的差异,有很多空报、漏报情况。需要许多学者为数值模式的改进提供较为准确的代表性区域的参数计算方法或者实测值及计算值。本文基于此目的,结合实验观测给出塔里木盆地多种沙源类型沙通量的计算值,以期为相关数值模式预报参数化方案的改进、为沙尘天气预报准确率的提高尽微薄之力。
1 资料与方法
1.1 观测场概况
在沙漠地区研究沙尘天气及近地层沙尘物质的运动特征、物理过程、起沙参数需要长期的、实时的观测数据,基础性科研成果的获取必须基于长期系统的基础性观测研究。中国气象局乌鲁木齐沙漠气象研究所先后于2008年7月在塔中沙漠腹地、2008年9月在肖塘沙漠北缘过渡带、2009年6月在若羌绿洲边缘沙地、2010年5月在策勒绿洲荒漠过渡带、塔里木盆地不同沙尘源地建立了4个风沙观测试验场,获取了宝贵的塔里木盆地多种沙源类型的实时观测数据,用于科研基础研究。其中,塔中风沙观测场(38°58′N,83°39′E,海拔1 082m)深入塔克拉玛干沙漠腹地220km,该地区地表为流沙覆盖,植被覆盖度极低。地貌以沙丘地貌为主,沙丘地貌表现为一系列线状的高大复合型纵向沙垄与垄间地相间分布,沙垄走向为NNE—SSW或EN—SW方向,相对高度为40~50m。垄间平坦沙地宽1~3km,长2~5km。高大沙垄的前缘分布有低矮的新月形沙丘和沙丘链。观测场设在两大沙垄间的平坦沙地上。该地区地表沙源的平均粒径为136μm[16],且分选情况较好。肖塘风沙观测场(40°49′N,84°17′E,海拔1 099m)地处塔克拉玛干沙漠北缘荒漠过渡带上,下垫面为平坦的风蚀裸露古河床。往北2km为胡杨林,西距沙漠公路约1km,周围有新月形沙丘和复合型新月形沙丘链,一般宽6~15m,高1~10m。复合型沙丘单体走向为NW—SE,其间广泛分布有土平地、风蚀残丘等地貌类型。该区域地表沙源平均粒径为159 μm[16],由于地处沙漠边缘过渡带和下伏河床沉积土,沙样分选较差。若羌风沙观测场位于若羌绿洲边缘的沙地上(39°24′N,88°15′E,海拔798m),观测场周边地势平坦开阔,地表裸露。地表沙粒较细且均匀,平均粒径仅103μm[16],分选比较好。策勒风沙观测场(37°02′37″N,80°40′52″E,海拔1 328m),地势平坦开阔,地表状况为自然平沙地,周边自然分布灌丛沙包,平均粒径仅115μm[16],分选比较好。
1.2 仪器与数据获取
塔中、肖塘、策勒和若羌风向、风速数据来自MetOne公司生产的010C/020C风速/风向传感器。观测场实地安装高度为5,10,20,50,100,200cm,风向安装高度为20,200cm,在200cm高度安装有空气温湿度传感器,用于监测沙尘天气过程中贴地层风速廓线特征。H11—LIN型风蚀传感器由美国Sensit公司生产,可以更加精细化地监测、研究地表沙粒活动。观测场实地传感器的安装高度为5,10cm,可测量沙尘天气过程的沙尘撞击颗粒数、撞击动能及沙粒运动速度,风蚀传感器上端有一个环状压电式晶片(直径为25mm,高为13mm),当沙粒撞击在晶片上时,会输出脉冲信号给数据采集器,记录下撞击颗粒的数目,并记为一次跃移活动,数据采集频率设为1 Hz。经过实验室标定Sensit对直径大于50μm沙粒的撞击具有很好的反应。Sensit传感器经过长期野外试验验证,对地表沙粒跃移运动的测量效果良好,结合贴地层风速梯度仪,可求出沙尘天气过程的起沙临界摩擦速度。塔中、若羌、肖塘和策勒平均粒径的计算使用英国Malvern公司生产的Mastersizer 2000型激光粒度仪进行测量,粒度参数计算方法如下:

粒度参数指从累积曲线上求出来的能表示样品粒度分布特征的数值,例如横坐标为粒径大小,纵坐标为粒度频率累积分布即为累积百分含量。样品累积曲线中的5%处的粒径大小并换算为φ值即可用φ5表示,其他以此类推。
由于各个风沙观测场地域以及仪器损坏等原因,本文以实际观测已有的资料为基础,通过撞击颗粒数连续性强,数据稳定等特点分别遴选出4个风沙观测场代表性沙尘暴过程,塔中(2009年5月26日)、肖塘(2009年7月17日)、若羌(2010年5月8日)、策勒(2010年8月24日)的一个对时数据作为样本分析。本文考虑到由于地域和天气的差异,下垫面条件的不同,做垂直沙通量与水平沙通量的横向比较的可比性不强,因此给出风速参考标准,可以界定在贴地面同等高度,同等风速条件下各个实验区域沙尘通量方向上的差别。
1.3 沙通量计算方法与临界摩擦速度
沙尘通量可以分为水平沙尘通量,即输沙率与垂直输沙通量,分别用Q与F表示,Q的物理意义是与水平风向垂直从地表到观测高度范围内单位宽度单位时间通过的沙粒质量,Q是沙粒漂移强度q(z)沿高度的积分[17];F的物理意义是某一高度处与地表面平行的单位面积内单位时间地表向大气中输送的尘粒质量[15]。关于沙通量的量纲国内外研究尚未统一,本文为了方便,均采用国际通用单位kg/(m·s)表示。关于水平沙尘通量Q(输沙率)的计算方法,国内外很多学者通过大量的野外观测研究与风洞模拟研究总结出各自的计算公式(表1),根据塔中地区实测沙尘通量与理论沙尘通量的比较,Bagnold与Zingg公式的结果都比实测的要偏小,Zingg的结果最小,而Kawamura公式的结果则偏大,只有Lettau公式的计算结果与实测最接近,风速20.0m/s以下的时候,两条曲线几乎重合,当风速大于20.0m/s的时候,实测结果又比Lettau的结果稍微偏大,不过仍然很接近[18],因此本文计算水平输沙量Q时采用Lettau公式。关于垂直输沙通量F的计算,Lu等[19]、Marticorena等[20]、Shao[21-22]、Gillette等[23]都进行了研究,并建立了自己的计算模型。其中Lu、Marticorena和Shao的输沙通量模式理论较为完善,但是模式形式比较复杂,计算中需要的参数较多且有的参数很难确定,实际运用中有很大难度,而Gillette等的计算方案在形式上非常简单,只需要u*和u*t两个参数,比较适合简单或近似的估算,因此本文计算垂直输沙量F时采用Gillette等公式,其公式具体如下:
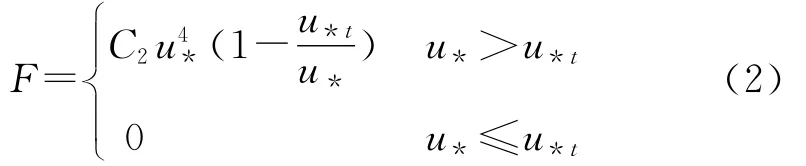
根据风蚀传感器中的计算公式本文将摩擦速度的计算公式做简单变换,具体如下:

式中:k——卡曼常数取值0.4;z——高度取值2m;u——z处即2m高的风速;z0——地表粗糙度。鉴于策勒、若羌风沙观测场所获取的数据无法计算z0,本文考虑策勒、若羌与塔中自然平缓沙地上(B站)标校自动站地表状况相似,因此利用西侧2.2km处的两层风、温同步资料,对塔中地区的地表粗糙度长度z0进行确定。计算得出年平均粗糙长度z0为1.175×10-4m。塔克拉玛干沙漠北部肖塘地区年平均粗糙度为6.05×10-5m[24],C2是经验常数,近似取1.4×10-15g·cm-6·s3。

表1 代表性输沙率模型
塔中、肖塘、若羌3地的临界摩擦速度分别在0.25,0.27,0.21m/s左右时,地表有沙粒起动。因此可以近似地认为塔中、肖塘、若羌3地的临界摩擦速度分别为0.25,0.27,0.21m/s[25]。如图1所示,根据H11—LIN型风蚀传感器所测得的撞击颗粒数与摩擦速度做相关计算得出策勒的临界摩擦速度为0.22m/s。
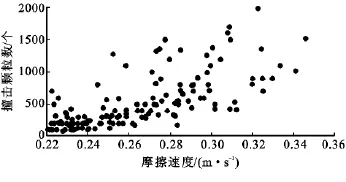
图1 策勒风蚀传感器所测的摩擦速度与颗粒撞击数的关系
2 结果与分析
在以下的表述过程中,参数单位统一为国际标准单位的量纲kg/(m·s),F量级为10-8kg/(m2·s),Q的量级为10-4kg/(m·s),为了方便比较分析,下述的F和Q省略单位和量级。由图2—5可知,垂直沙通量的分布时间段多集中于白天及午后,这与沙尘暴多发于这一时间段有关。若羌的垂直沙通量F要明显大于策勒、肖塘、塔中等地区。在地面2m出风速达到2m/s时,若羌F值接近于50,最大,策勒在7.5左右次之,塔中和肖塘比较接近于3左右;在贴地面2m处的风速达到6m/s时,若羌F值达到150最大,策勒F为20,塔中F为10,肖塘F为10。由于起沙量的大小主要取决于风速和沙粒粒径,肖塘本地的沙尘粒径要小于塔中,在风速大小基本一致的情况下,垂直沙通量F却大致相同,这很好的印证了垂直沙通量F还受到下垫面、地形以及地表土壤含水率等因素的影响。4个站垂直沙通量F与风速都表现出较好的线性相关,风速递增,垂直沙通量递增;风速递减,垂直沙通量递减。

图2 2010年5月8日若羌垂直沙通量F与风速日变化
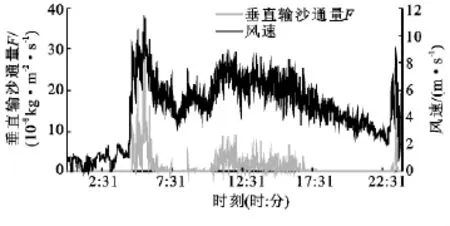
图3 2010年8月24日策勒垂直沙通量F与风速日变化

图4 2010年7月17日肖塘垂直沙通量F与风速日变化
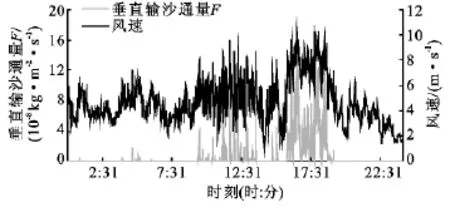
图5 2010年5月26日塔中垂直沙通量F与风速日变化
从图6—9可知,水平沙尘通量Q与实测2m处风速具有一致性,水平沙尘通量Q值随风速的变化而变化,水平沙尘通量Q集中在天气过境时,时间节点多在午后,为沙尘暴的高发时段。整个水平沙尘通量的量级要大于垂直沙尘通量。当贴地面风速在2 m/s左右时,若羌Q值在100左右,策勒Q值在40左右,塔中和肖塘在20左右,塔中Q值稍大;当贴地面的风速在4m/s时,若羌Q值在300左右,策勒Q值在80左右,塔中和肖塘在40左右,塔中Q值较大;当贴地面的风速在6m/s时,若羌Q值在400左右,策勒Q值在125左右,塔中Q值在70左右和肖塘Q值在65左右。可见在相同风速下,若羌Q值最大,策勒次之,塔中第三,肖塘最小。在风速递增幅度相同条件下,若羌Q值递增幅度最大,策勒次之,塔中、肖塘基本相同。当贴地面风速递增2m/s,若羌的Q值递增速率约为100,策勒约为40,塔中、肖塘约为20。临界摩擦速度、粒径、风速、土壤含水量都是输沙量的决定性因素,在本文4个实验区域中风速等同条件下,沙地的土壤含水率基本相同,值趋于零,临界摩擦速度及粒径大小成为主导因素,在若羌临界摩擦速度最小,策勒较大,塔中第三,肖塘最大的条件下,沙尘通量值出现了上述结果。但是平均粒径只代表这一区域的平均状况,并不能较好地诠释相对细颗粒和相对粗颗粒的百分比含量,每次过程采样也不能完全界定其大小,存在一定难度,所以平均粒径大小的影响程度只能作为定性参考,定量化计算尚需努力。

图6 2010年5月8日若羌水平沙通量Q与风速日变化

图7 2010年5月24日策勒水平沙通量Q与风速日变化
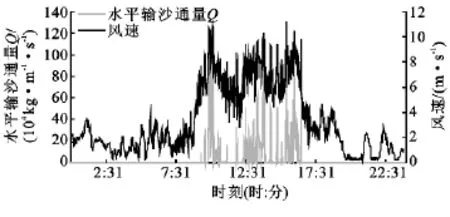
图8 2010年7月17日肖塘水平沙通量Q与风速日变化

图9 2010年5月26日塔中水平沙通量Q与风速日变化
3 结论
塔里木盆地多种沙源类型的沙尘通量(F与Q)值均与实测2m处风速变化趋势一致,水平沙尘通量的量级要大于垂直沙尘通量。在相同风速下,若羌沙尘通量最大,策勒次之,塔中第三,肖塘最小。在风速递增幅度相同条件下,若羌水平沙尘通量递增幅度最大,策勒次之,塔中、肖塘基本相同。本文沙通量的计算值与杨兴华[15]相较,F与Q 的量级处于同一水平,F值相近,Q值稍小;与成天涛[7]相较,塔里木盆地输沙量要大于浑善达克沙地,这是由临界起沙风速较小,粒径较细引起的;与申彦波[12]相较,塔里木盆地4个代表站点的F与Q平均值的量级分别为10-8kg/(m2·s),10-4kg/(m·s)与敦煌戈壁计算的顺风向沙粒通量和垂直尘粒通量平均值的量级一致。
4 讨论
就本文采用的计算输沙量的方法而言,临界摩擦速度、粒径、风速都是输沙量的决定性影响因素,风的动力作用不仅仅表现为风速、风向数值的变化,还有很多间接作用。风可以塑造沙丘的形态,风是大自然的搬运工,沙尘粒度的组份,与风的起动与迁移有着重要的联系,沙尘颗粒能否被搬运,很大程度上取决于风速的大小。沙尘粗颗粒不能长期在空气中悬浮搬运,大部分在地面跳跃迁移,沙尘细颗粒或者极细颗粒可以随风做长途悬浮搬运,假设研究区域的盛行风向具有较好的一致性,那么沙地长期风化的结果就是平均粒径增大,导致输沙量减小。临界摩擦速度与输沙量成反比关系,粒径与输沙量成反比关系,而风速与输沙量为正比关系,但是临界摩擦速度取值与粒径值与风速又有着较为复杂的关系,还有其它影响要素,如液态或者固态降水改变了表层土壤含水率从而导致临界摩擦速度增大,输沙量减小。不同于临界起沙风速,地面起沙率和垂直起沙障碍物高度的增大而减少,另外植物株间距或障碍物间距也是一个重要的影响因素[7]。因此,输沙量的很多计算公式都是经验性的总结,鉴于各个研究区域下垫面环境的差异性及地表形态微变化,所有的经验性公式都有着自己的适用性和局限性。风蚀起沙的临界摩擦速度、起沙风速以及沙尘通量,也随着天气系统动力、热力条件改变而改变、也随着地表状况变化而变化。因此,沙通量变化不确定性会直接影响到沙尘数值预报模式的参数化方案的改进,期望能通过大量的野外试验来确定和验证沙通量的变化阈值。
在沙尘暴数值预报模式中,u*t是判定起沙过程的重要参量,一般通过参数化方案实时计算得出。本文所计算的u*t是典型地点典型过程的临界摩擦速度。通过对同一次过程野外试验获取的u*t和模式计算出的u*t进行比较,找出其中的差异,探索其原因,从而可为模式相关参数化方案的优化提供依据。水平沙尘通量Q计算方案的选取本身就是一个与实验结合的检验工作,本文利用Lettau水平沙尘通量公式正是我们研究团队在典型沙尘暴过程中实测收集的结果与多种计算方案拟合检验后的最优选取,可为改进沙尘暴数值模式沙尘通量预报参数化方案提供参考。
[1] 魏文寿,崔彩霞,尚华明,等,译.沙漠气象学[M].北京:气象出版社,2008.
[2] Bagnold R A.The Physics of Blown Sand and Desert Dunes[M].London:Methuen,1941.
[3] Shao Yaping.Physics and Modeling of Wind Erosion[M].Sydney:Kluwer Academic Publishers,2000.
[4] Dong Zhibao,Liu Xiaoping,Wang Hongtao,et al.The flux profile of a blowing sand cloud:a wind tunnel investigation[J].Geomorphology,2002,49(3/4):219-230.
[5] 李万源,沈志宝,吕世华,等.风蚀影响因子的敏感性试验[J].中国沙漠,2007,27(6):985-993.
[6] 沈志宝,申彦波,杜明远,等.沙尘暴期间戈壁沙地起沙率的观测结果[J].高原气象,2003,22(6):545-550.
[7] 成天涛,吕达仁,徐永福.浑善达克沙地起沙率和起沙量的估计[J].高原气象,2006,25(2):236-241.
[8] 陈渭南,董治宝,杨佐涛,等.塔克拉玛干沙漠的起沙风速[J].地理学报,1995,50(4):360-367.
[9] Gillette A D,Ranjit P.Modeling dust emission caused by wind erosion[J].Journal of Geophysical Research,1988,93(11):14234-14242.
[10] 梅凡民,张小曳,鹿化煜,等.若干风蚀粉尘释放模型述评[J].中国沙漠,2004,24(6):791-796.
[11] 王鹏祥,孙兰东,岳平,等.盐池地区沙尘暴期间风沙运动若干特征研究[J].中国沙漠,2007,27(6):1077-1079.
[12] 申彦波,沈志宝.敦煌戈壁地表风蚀起沙量的计算[J].高原气象,2004,23(5):648-653.
[13] 申彦波,沈志宝,杜明远,等.风蚀起沙的影响因子及其变化特征[J].高原气象,2005,24(4):613-616.
[14] 李江风.沙漠气候[M].北京:气象出版社,2002.
[15] 杨兴华,何清,艾力·买买提明.塔中地区一次沙尘暴过程的输沙通量估算[J].干旱区研究,2010,27(6):971-974.
[16] 霍文,何清,刘新春,等.塔克拉玛干沙漠及其大气降尘点粒度特征分析[J].水土保持研究,2009,16(4):207-211.
[17] 杨兴华,何清,艾力·买买提明.塔克拉玛干沙漠塔中地区春夏季风蚀起沙研究[J].中国沙漠,2010,30(4):770-776.
[18] 杨兴华.塔克拉玛干沙漠塔中地区春夏季沙粒运移及动力参数研究[D].乌鲁木齐:新疆师范大学,2009.
[19] Lu Hua,Shao Yaping.A new model for dust emission by saltation bombardment[J].Journal of Geophysical Research,1999,104(14):16827-16841.
[20] Marticorena B,Bergametti G,Aumont B,et al.Modeling the atmospheric dust cycle.Part 2:simulation of Saharan dust sources[J].Journal of Geophysical Research,1997,102(4):4387-4404.
[21] Shao Y,Raupach M R,Findlater P A.Effect of saltation bombardment on the entrainment of dust by wind[J].Journal of Geophysical Research,1993,98(7):12719-12726.
[22] Shao Yaping,Lu Hua.A simple expression for wind erosion threshold friction velocity[J].Journal of Geophysical Research,2000,105(17):22437-22443.
[23] 何清,缪启龙,张瑞军,等.塔克拉玛干沙漠肖塘地区空气动力学粗糙度分析[J].中国沙漠,2008,28(6):1011-1016.
[24] 何清,杨兴华,艾力·买买提明.塔克拉玛干沙漠风蚀起沙观测研究[J].中国沙漠,2011,31(2):315-322.
